Loading AI tools
Групи сферичної симетрії також називають точковими групами в тривимірному просторі, однак у цій статті розглянуто тільки скінченні симетрії. Існує п'ять фундаментальних класів симетрії, притаманних трикутним фундаментальним областям: діедрична, циклічна, тетраедрична, октаедрична[en] та ікосаедрична симетрія.
 Симетрії-інволюції Cs, (*) [ ] = |
 Циклічна симетрія Cnv, (*nn) [n] = |
 Діедрична симетрія Dnh, (*n22) [n,2] = | |
| Групи многогранників, [n,3], (*n32) | |||
|---|---|---|---|
 Тетраедрична симетрія Td, (*332) [3,3] = |
 Октаедрична симетрія Oh, (*432) [4,3] = |
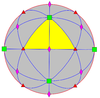
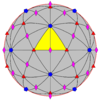
 Ікосаедрична симетрія Ih, (*532) [5,3] = | |
В статті перелічено групи згідно з символами Шенфліса, нотацією Коксетера[en][1], орбіфолдною нотацією[en][2] і порядком. Конвей використовував варіант запису Шенфліса, заснований на алгебраїчній структурі групи кватерніонів, з позначеннями однією або двома великими літерами і повним набором нижніх числових індексів. Порядок групи позначається індексом, якщо тільки він не подвоюється символом плюс-мінус («±»), який передбачає центральну симетрію [3].
Також наведено символіку Германа — Могена (міжнародна нотація). Групи кристалографії, загалом 32, є підмножиною з елементами порядку 2, 3, 4 і 6[4].
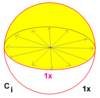
Є чотири симетрії, які є оберненими собі, тобто інволюціями: тотожне перетворення (C1), дзеркальна симетрія (Cs), обертова симетрія (C2), і центральна симетрія (Ci).
| Міжн. | Геом. | Орб. | Шенф. | Конвей | Кокс. | Пор. | Фунд. область |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 11 | C1 | C1 | ][ [ ]+ |
1 |  |
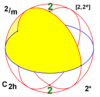
| 2 | 2 | 22 | D1 = C2 |
D2 = C2 |
[2]+ | 2 |  |
Існують чотири нескінченних сімейства циклічної симетрії[en] з n=2 і вище (n може дорівнювати 1 як особливий випадок немає симетрії).
Існує три нескінченних сімейства з діедричною симетрією[en] з n рівним 2 і більше (n може дорівнювати 1 як особливий випадок).
| Міжн. | Геом. | Орб. | Шенф. | Конвей | Кокс. | Пор. | Фунд. область |
|---|---|---|---|---|---|---|---|
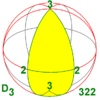
| 222 | 2.2 | 222 | D2 | D4 | [2,2]+ | 4 |  |
| 42m | 42 | 2*2 | D2d | DD8 | [2+,4] | 8 |  |
| mmm | 22 | *222 | D2h | ±D4 | [2,2] | 8 |  |
Існує три типи симетрії многогранників[en]: тетраедрична симетрія, октаедрична симетрія[en] і ікосаедрична симетрія, названі за правильними многогранниками з трикутними гранями, які мають відповідні симетрії.
| Міжн. | Геом. | Орб. | Шенф. | Конвей | Кокс. | Пор. | Фунд. область |
|---|---|---|---|---|---|---|---|
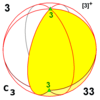
| 23 | 3.3 | 332 | T | T | [3,3]+ = [4,3+]+ |
12 |  |
| m3 | 43 | 3*2 | Th | ±T | [4,3+] | 24 |  |
| 43m | 33 | *332 | Td | TO | [3,3] = [1+,4,3] |
24 |  |
- Кристалографічна точкова група симетрії
- Група трикутника
- Список планарних груп симетрії[en]
- Точкові групи у двовимірному просторі[en]
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.