دالة متباينة

في الرياضيات، الدالة المتباينة (بالإنجليزية: Injective function) هي دالة تبقى بها العناصر متباينة (متفاوتة): فبها لا تقترن العناصر المتباينية من مجالها بنفس العنصر من مجالها المقابل. بمعنى أن كل عنصر من مجالها المقابل مقترن بعنصر من مجالها واحد على الأكثر.

دالة متباينة ولكنها غير غامرة (ليست بدالة تقابلية)

دالة متباينة وغامرة في آن واحد (هي دالة تقابلية)

دالة غير متباينة ولكنها غامرة

تعريف

لتكن f دالة مجال تعريفها هو مجموعة A. الدالة f هي متباينة إذا وفقط إذا توفر لكل عنصرين a و b من A ما يلي:

إذا كان (f(a) = f(b، فإن a = b؛ أي أن (f(a) = f(b تعني a = b. وبشكل مكافئ، إذا كان a ≠ b، فإن (f(a) ≠ f(b.

باستعمال رموز الرياضيات، يُحصل على ما يلي:

${\displaystyle \forall a,b\in A,\;\;f(a)=f(b)\Rightarrow a=b}$

والتي تكافئ بشكل منطقي ما يلي:

${\displaystyle \forall a,b\in A,\;\;a\neq b\Rightarrow f(a)\neq f(b)}$

أمثلة

• الدالة المطابقة هي دالة متباينة.
• الدالة f : R → R المعرفة ب f(x) = 2x + 1 هي متباينة.

• 
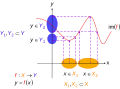
  دوال متباينة. تفسير هندسي في نظام إحداثي ديكارتي, المعرفة بالتطبيق f : X → Y, حيث y = f(x), X = مجال دالة, Y = مدى دالة, و im(f) يرمز إلى صورة of f. Every one x في X maps to exactly one unique y in Y. الأجزاء المدورة من المحورين تمثل domain و range sets – في توافق مع المخططات المستعملة في التعريف أعلاه.
• 
  دالة غير متباينة. في هذه الحالة X₁ و X₂ هما مجموعتان جزئيتان من X, Y₁ و Y₂ are مجموعتان جزئيتان من Y: for two regions حيث الدالة غير متباينة لأن more than one domain عنصر can map to a single range element. That is, it is possible for more than one x في X to map to the same y في Y
• 
  Making functions injective. الدالة السابقة f : X → Y can be reduced to one or more injective functions (say) f : X₁ → Y₁ و f : X₂ → Y₂, shown by solid curves (long-dash parts of initial curve are not mapped to anymore). Notice how the rule f has not changed – only the domain و range. X₁ و X₂ are مجموعتان جزئيتان من X, Y₁ و Y₂ هما مجموعتان جزئيتان من R: for two regions حيث الدالة الأولى can be made متباينة so that one domain element can map to a single range element. هكذا, only one x في X maps to one y في Y.