أفضل الأسئلة
الجدول الزمني
الدردشة
السياق
فرضية ريمان
مسألة غير محلولة في الرياضيات من ويكيبيديا، الموسوعة الحرة
Remove ads
فرضية ريمان (بالإنجليزية: Riemann hypothesis) هي حدسية حدسها سنة 1859م عالم الرياضيات الألماني برنارد ريمان.[1][2][3] تعتبر هذه المسألة من أعظم المسائل وأقدمها ومن أصعب الفرضيات التي استعصت على البرهان.
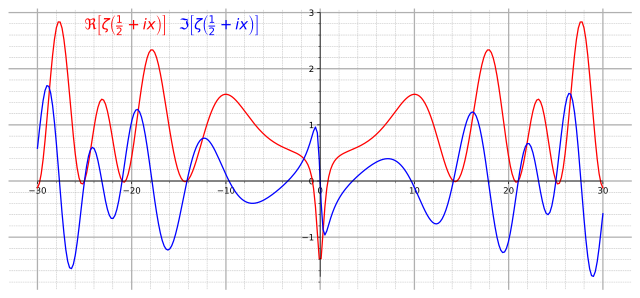
دالة زيتا معرفة بالنسبة لجميع الأعداد العقدية المختلفة عن 1. جميع الأعداد الزوجية السالبة(2-, 4-, 6-, ...) هي جذور لهذه الدالة وتسمى «جذورا بديهية». فرضية ريمان تتعلق بالجذور غير البديهية وتقول :
- الجزء الحقيقي للجذور غير البديهية للدالة زيتا هو 1/2.
تعتبر هذه الحدسية أحد المسائل الأكثر أهمية في الرياضيات الحالية، حيث جاءت ثامنَ مسائل هيلبرت المشهورة التي نُشرت سنة 1900م. كما أنها إحدى المسائل السبع التي اختارتها مؤسسة كلاي سنة 2000م, المعروفة ب مسائل الألفية والتي حددت جائزة مالية لحلها. فرضية ريمان هي المسألة الوحيدة المشتركة بين هاتين اللائحتين.
تتعلق فرضية ريمان بدالة أبدعها ريمان منذ حوالي قرن ونصف واسمها دالة زيتا لريمان. تنص الفرضية على أن الجزء الحقيقي للجذور العقدية لهذا التابع ثابت دوماً ويساوي النصف. جرت محاولات كثيرة خلال قرن ونصف لإثبات الفرضية ولم تكلل بالنجاح. مسألة تقرير وضع الفرضية (من الصحة أو الخطأ أو استحالة إثبات بالرياضيات الحالية).
حل هذه الفرضية يساهم في فهم توزيع الأعداد الأولية.
Remove ads
دالة زيتا لريمان
الملخص
السياق
دالة زيتا لريمان تعرف بالنسبة لعدد عقدي ، جزئه الحقيقي أكبر قطعا من 1 بالمتسلسلة غير المنتهية والمتقاربة مطلقا، التالية:
أثبت ليونهارد أويلر أن هذه المتسلسلة تساوي جداء أويلر والمعرف بما يلي :
حيث يشمل هذا الجداء غير المنتهي جميع الأعداد الأولية، وأيضا، يؤول إلى عدد معين عندما يكون الجزء الحقيقي ل أكبر قطعا من 1. كون جداء أويلر متقاربا عندما يكون الجزء الحقيقي ل أكبر قطعا من الواحد، يعني أنه ليس للدالة جذرا في هذه المنطقة.
تتعلق فرضية ريمان بالجذور الواقعة خارج المنطقة التي تكون فيها هاته المتسلسلة متقاربة، ولهذا السبب، فإنه ينبغي لدالة زيتا لريمان أن تُمدد تحليليا إلى جميع الأعداد العقدية. انظر إلى دالة إيتا لدركليه.
دالة زيتا لريمان تستوفي المعادلة الدالية الآتية :
Remove ads
الأصل
السبب الذي دفع ريمان لدراسة الدالة زيتا وجذورها هو إرتباطها بالصيغة الكاملة للدالة المعدة للأعداد الأولية ، التي تقوم بحساب عدد الأعداد اللأعداد الأولية الأقل من عددٍ ما . والتي قام بنشرها في ورقته عام 1859 «حول عدد الأعداد الأولية الأقل من مقدار محدد». الصيغة الكاملة ل هي :
.
بحيث أن هي الجذور غير البديهية لدالة زيتا لريمان، بالنسبة ل طالع دالة التكامل اللوغاريتمي.
Remove ads
نتائج
الملخص
السياق
توزيع الأعداد الأولية
إذا كانت فرضية ريمان صحيحة فإن قيمة الخطأ بين التكامل اللوغاريتمي لأويلر و (انظر إلى الدالة المعدة للأعداد الأولية وإلى أعمال هيلغ فون كوخ في هذا المجال) تستوفي المتفاوتة الآتية :
لكل .
نمو الدوال الحسابية
فرضية ريمان تفرض حدودا قصوى على مجموعة من الدوال الحسابية بالإضافة إلى الدالة المعدة للأعداد الأولية المتحَدث عنها أعلاه.
من الأمثلة على ذلك، دالة موبيوس . كون المعادلة التالية:
صحيحة عندما يكون الجزء الحقيقي ل أكبر قطعا من النصف، مع كون المجموع الموجود في يمين المعادلة متقاربا، يكافئ فرضية ريمان. نتيجة لذلك، يُمكن أن يُستنتج أنه إذا عُرفت دالة ميرتنز كما يلي:
إذن فإن القول بأن
بالنسبة لأي عدد موجب يكافئ فرضية ريمان. (انظر إلى رمز O الكبير)
الهندسة غير التبادلية
في عامي 1999 و 2000، وصف ألان كن علاقة بين فرضية ريمان والهندسة غير تبديلية.
Remove ads
الجذور على المستقيم الحرج
الملخص
السياق
بداية القرن العشرين، برهن غودفري هارولد هاردي وجون إيدنسور ليتلوود على أن هناك عددا لا نهائي من الأصفار لدالة زيتا على المستقيم الحرج.
حسابات عددية
Remove ads
مراجع
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads
















