مصفوفة تجاور

في نظرية البيان وعلوم الحاسوب، مصفوفة التجاور^[1] أو المجاورة (بالإنجليزية: Adjacency Matrix) هي مصفوفة مربعة تستخدم لتمثيل البيان. عناصر المصفوفة تعكس ما إذا كانت رؤوس البيان متجاورة ومرتبطة أم لا.

أمثلة

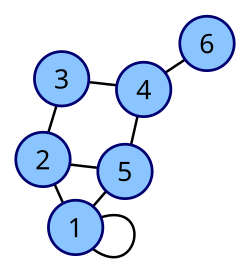
البيانات ومصفوفات التجاور المقابلة المبينة هنا تشير بأن كل وصلة يربط نقطتين يضيف العدد "1" وكل حلقة داخلية تُضيف "2" آخر. هذا يسمح بمعرفة درجة ارتباط كل نقطة مع النقاط الأخرى عبر أخذ مجموع ارتباطات كل نقطة بغيرها أو مع نفسها (حلقة). فمثلا العنصر الأول في المصفوفة (1,1)A له القيمة 2 وهي بسبب الحلقة الدائرية على النقطة الأولى والعنصر (1,2)A  له القيمة 1 لارتباط الرأسين <1> و <2> بضلع واحد وفي حالة عدم التجاور يأخذ عنصر المصفوفة القيمة صفر.

بيان محدد	مصفوفة التجاور
	${\displaystyle {\begin{pmatrix}2&1&0&0&1&0\\1&0&1&0&1&0\\0&1&0&1&0&0\\0&0&1&0&1&1\\1&1&0&1&0&0\\0&0&0&1&0&0\\\end{pmatrix}}}$ عناصر مصفوفة التجاور ذات البعد 6x6
بيان ناورو	احدائيات العناصر من 0 إلى 23 حيث النقاط البيضاء تشير لعدم المجاورة (القيمة صفر) وشدة اللون تُشير إلى تزايد الترابط.
بيان موجه لِكايلي S4	بيان موجه المعروف ببيان كايلي الموجه.

البيانات التافهة

تحتوي مصفوفة التجاور للبيان الكامل فقط على العدد 1 في ما عدا الخط على طول القطر الذي توجد فيه أصفار فقط. مصفوفة التجاور لبيان صفري^{[الإنجليزية]} مصفوفة صفرية.^[2][3]

انظر أيضا

• مصفوفة لابلاس