Айырым сығарылма

Математик анализда айырым сығарылма (беренсе сығарылма) (рус. Частная производная) — сығарылма төшөнсәһенең бер нисә үҙгәреүсәнле функция осрағына дөйөмләштереүҙәренең береһе. Айырым сығарылма — ул һайланған үҙгәреүсән буйынса функцияның артымының был үҙгәреүсәндең артымына сағыштырмаһының, был артым нулгә ынтылғандағы сикләнмәһе.

Айырым сығарылма
Ҡайҙа өйрәнелә	Күп үҙгәреүсәнле функция анализы
Закон йәки теорема формулаһы	${\displaystyle {\frac {\partial }{\partial x}}f(\dots ,x,\dots )=\lim _{h\to 0}{\frac {f(\dots ,x+h,\dots )-f(\dots ,x,\dots )}{h}}}$
Обозначение в формуле	${\displaystyle {\frac {\partial }{\partial x}}}$, ${\displaystyle f}$ һәм ${\displaystyle \lim }$
Тамғалау	айырым сығарылма символы[d]
Вики-проект	Проект:Математика[d]

Был терминдың башҡа мәғәнәләре лә бар, ҡарағыҙ: Производная.

${\displaystyle f}$ функцияһының ${\displaystyle x}$ үҙгәреүсәне буйынса айырым сығарылмаһы ғәҙәттә ${\displaystyle {\tfrac {\partial f}{\partial x}}}$, ${\displaystyle f_{x}}$ йәки ${\displaystyle D_{x}f}$ тип тамғалана. Үҙгәреүсәндәр нумерланған осраҡта, мәҫәлән ${\displaystyle x_{1},\dots ,x_{n}}$, шулай уҡ ${\displaystyle f_{i}}$ һәм ${\displaystyle D_{i}f}$ тамғалауҙары ҡулланыла.

${\displaystyle f(x_{1},x_{2},\ldots ,x_{n})}$ функцияһының ${\displaystyle (a_{1},a_{2},\ldots ,a_{n})}$ нөктәһендә айырым сығарылмаһы ошолай билдәләнә:

${\displaystyle {\frac {\partial f}{\partial x_{k}}}(a_{1},\cdots ,a_{n})=\lim _{\Delta x\to 0}{\frac {f(a_{1},\ldots ,a_{k}+\Delta x,\ldots ,a_{n})-f(a_{1},\ldots ,a_{k},\ldots ,a_{n})}{\Delta x}}.}$

Оператор \ Функция	${\displaystyle f(x)}$	${\displaystyle f(x,y,u(x,y),v(x,y))}$
Дифференциал	1: ${\displaystyle \operatorname {d} \!f=f'_{x}\operatorname {d} \!x}$	2: ${\displaystyle \operatorname {d} _{x}\!f=f'_{x}\operatorname {d} \!x}$ 3: ${\displaystyle \operatorname {d} \!f=f'_{x}\operatorname {d} \!x+f'_{y}\operatorname {d} \!y+f'_{u}\operatorname {d} \!u+f'_{v}\operatorname {d} \!v}$
Айырым сығарылма (беренсе сығарылма)	${\displaystyle f'_{x}{\overset {\underset {\mathrm {(1)} }{}}{=}}{\frac {\operatorname {d} \!f}{\operatorname {d} \!x}}}$	${\displaystyle f'_{x}{\overset {\underset {\mathrm {(2)} }{}}{=}}{\frac {\operatorname {d} _{x}\!f}{\operatorname {d} \!x}}={\partial f \over \partial x}}$
Тулы сығарылма (икенсе сығарылма)	${\displaystyle {\frac {\operatorname {d} \!f}{\operatorname {d} \!x}}{\overset {\underset {\mathrm {(1)} }{}}{=}}f'_{x}}$	${\displaystyle {\frac {\operatorname {d} \!f}{\operatorname {d} \!x}}{\overset {\underset {\mathrm {(3)} }{}}{=}}f'_{x}+f'_{u}{\frac {\operatorname {d} \!u}{\operatorname {d} \!x}}+f'_{v}{\frac {\operatorname {d} \!v}{\operatorname {d} \!x}};(f'_{y}{\frac {\operatorname {d} \!y}{\operatorname {d} \!x}}=0)}$

z = x² + xy + y² функцияһының графигы. (1, 1, 3) нөктәһендә айырым сығарылмаһы, y даими булғанда, xz яҫылығына параллель тейеүсе тура һыҙыҡтың ауышлыҡ мөйөшөнә тап килә.

Юғарыла һүрәтләнгән графиктың y = 1 яҫылығы менән киҫелештәре

Тамғалау

Иғтибар итергә кәрәк, ${\displaystyle {\frac {\partial f}{\partial x}}}$ тамғалауын, ${\displaystyle {\frac {df}{dx}}}$ - функцияның бер үҙгәреүсәндән ғәҙәттәге сығарылмаһынан айырмалы рәүештә, бөтөн символ итеп аңларға кәрәк, уны функцияның һәм аргументтың дифференциалдарының сағыштырмаһы итеп күрһәтергә мөмкин. Ләкин, айырым сығарылманы ла дифференциалдар сағыштырмаһы итеп күрһәтергә мөмкин, әммә был осраҡта мотлаҡ рәүештә функцияның артымы ниндәй үҙгәреүсән буйынса башҡарыла икәнен күрһәтергә кәрәк: ${\displaystyle {\frac {\partial f}{\partial x}}\equiv {\frac {d_{x}f}{dx}}}$, бында ${\displaystyle d_{x}f}$ — ${\displaystyle f}$ функцияһының ${\displaystyle x}$ үҙгәреүсәне буйынса айырым дифференциалы. Йыш ҡына ${\displaystyle {\frac {\partial f}{\partial x}}}$ символының бөтөнлөгөн аңламау хаталарҙың һәм аңлашылмаусанлыҡтарҙың сәбәбе булып тора, мәҫәлән, ${\displaystyle {\frac {\partial f}{\partial x}}{\frac {\partial x}{\partial t}}}$ аңлатмаһында ${\displaystyle \partial x}$-ты ҡыҫҡартыу кеүек^[1].

Геометрик интерпретация

Геометрик, айырым сығарылма координаталар күсәрҙәренең береһе йүнәлеше буйынса сығарылманы бирә. ${\displaystyle f}$ функцияһының ${\displaystyle {\vec {x}}{\,}^{0}=(x_{1}^{0},\ldots ,x_{n}^{0})}$ нөктәһендә ${\displaystyle x_{k}}$ координатаһы буйынса айырым сығарылмаһы ${\displaystyle {\vec {e}}={\vec {e}}{\,}^{k}=(0,\ldots ,0,1,0,\ldots ,0)}$ йүнәлеше буйынса ${\displaystyle {\frac {\partial f}{\partial {\vec {e}}}}}$ сығарылмаһына тигеҙ, бында 1 ${\displaystyle k}$-сы урында тора.

Миҫалдар

Конустың күләме бейеклегенә һәм нигеҙенең радиусына бәйле

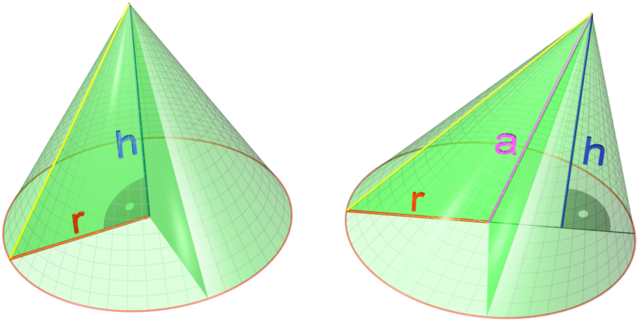
Конустың V күләме h бейеклегенә һәм r радиусына

${\displaystyle V={\frac {\pi r^{2}h}{3}}}$ формулаһына ярашлы бәйле

V күләменең r радиусына ҡарата айырым сығарылмаһы

${\displaystyle {\frac {\partial V}{\partial r}}={\frac {2\pi rh}{3}},}$

ул конустың, әгәр уның радиусы үҙгәрһә, ә бейеклеге үҙгәрешһеҙ ҡалһа, күләменең үҙгәреү тиҙлеген күрһәтә. Мәҫәлән, әгәр күләм үлсәү берәмеге ${\displaystyle m^{3}}$, ә оҙонлоҡ үлсәме ${\displaystyle m}$ тип иҫәпләгәндә, юғарыла күрһәтелгән сығарылма күләм үлсәме тиҙлеге үлсәмлегенә ${\displaystyle m^{3}/m}$ эйә буласаҡ, йәғни радиус дәүмәленең 1 ${\displaystyle m}$-гә үҙгәреүе конус күләменең ${\displaystyle {\frac {2\pi rh}{3}}}$ ${\displaystyle m^{3}}$-гә үҙгәреүенә тап килә.

h-ҡа ҡарата айырым сығарылма

${\displaystyle {\frac {\partial V}{\partial h}}={\frac {\pi r^{2}}{3}},}$

ул конустың, әгәр уның бейеклеге үҙгәрһә, ә радиусы үҙгәрешһеҙ ҡалһа, күләменең үҙгәреү тиҙлеген күрһәтә.

V-тың r һәм h-ҡа ҡарата тулы сығарылмаһы

${\displaystyle {\frac {\operatorname {d} V}{\operatorname {d} r}}=\overbrace {\frac {2\pi rh}{3}} ^{\frac {\partial V}{\partial r}}+\overbrace {\frac {\pi r^{2}}{3}} ^{\frac {\partial V}{\partial h}}{\frac {\operatorname {d} h}{\operatorname {d} r}}}$

һәм

${\displaystyle {\frac {\operatorname {d} V}{\operatorname {d} h}}=\overbrace {\frac {\pi r^{2}}{3}} ^{\frac {\partial V}{\partial h}}+\overbrace {\frac {2\pi rh}{3}} ^{\frac {\partial V}{\partial r}}{\frac {\operatorname {d} r}{\operatorname {d} h}}}$

Тулы һәм айырым сығарылма араһында айырма — һуңғыһында үҙгәреүсәндәр араһында ситләтелгән бәйлелекте бөтөрөүҙән ғибәрәт.

Әгәр (ниндәйҙер сәбәптәр буйынса) конустың пропорциялары үҙгәрешһеҙ ҡалһа, бейеклек һәм радиус билдәләнгән k нисбәтендә ҡалалар

${\displaystyle k={\frac {h}{r}}={\frac {\operatorname {d} h}{\operatorname {d} r}}.}$

Был r-ға ҡарата тулы сығарылманы бирә:

${\displaystyle {\frac {\operatorname {d} V}{\operatorname {d} r}}={\frac {2\pi rh}{3}}+k{\frac {\pi r^{2}}{3}}}$

Айырым сығарылмалар ингән тигеҙләмәләр айырым сығарылмаларҙа дифференциаль тигеҙләмәләр тип аталалар һәм физикала, инженерияла һәм башҡа фәндәрҙә һәм ғәмәли дисциплиналарҙа киң билдәлеләр.