Апісаная акружнасць

Апісаная акружнасць многавугольніка — акружнасць, якая змяшчае ўсе вяршыні многавугольніка. Яе цэнтр ёсць пункт перасячэння сярэдзінных перпендыкуляраў да старон многавугольніка.

Акружнасць, апісаная вакол многавугольніка

Уласцівасці

• Цэнтр апісанае акружнасці выпуклага n-вугольніка ляжыць у пункце перасячэння сярэдзінных перпендыкуляраў да яго старон. Як вынік: калі вакол n-вугольніка апісана акружнасць, то ўсе сярэдзінныя перпендыкуляры да ягоных старон перасякаюцца ў адным пункце (цэнтры акружнасці).
• Каля любога правільнага многавугольніка (усе вуглы роўныя) можна апісаць акружнасць, і прытым толькі адну.

Для трохвугольніка

Акружнасць, апісаная вакол трохвугольніка

• Каля трохвугольніка можна апісаць акружнасць, прытым толькі адну. Яе цэнтрам будзе пункт перасячэння сярэдзінных перпендыкуляраў.
• У востравугольнага трохвугольніка цэнтр апісанае акружнасці ляжыць унутры, у тупавугольнага — па-за межамі трохвугольніка, у прамавугольнага — на сярэдзіне гіпатэнузы.

• 
  Востравугольны
• 
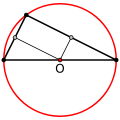
  Тупавугольны
• 
  Прамавугольны

Пазначым літарай О пункт перасячэння сярэдзінных перпендыкуляраў да ягоных старон і правядзём адрэзкі ОА, ОВ і ОС. Калі пункт О роўнааддалены ад вяршынь трохвугольніка АВС, то ОА = OB = ОС. Таму акружнасць з цэнтрам О радыуса ОА праходзіць праз усе тры вяршыні трохвугольнік і ў выніку з’яўляецца апісанай каля трохвугольніка ABC.

Радыус

Формулы радыуса апісанае акружнасці

• ${\displaystyle R={\frac {abc}{4S}}}$
• ${\displaystyle R={\frac {a}{2\sin \alpha }}={\frac {b}{2\sin \beta }}={\frac {c}{2\sin \gamma }}}$
• ${\displaystyle R={\frac {abc}{\sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}}={\frac {abc}{4{\sqrt {p(p-a)(p-b)(p-c)}}}},}$

дзе:

${\displaystyle a,b,c}$ — бакі трохвугольніка,

${\displaystyle \alpha ,\beta ,\gamma }$ — вуглы, процілеглыя да старон ${\displaystyle a,b,c}$ адпаведна,

${\displaystyle S}$ — плошча трохвугольніка.

${\displaystyle p}$ — паўперыметр трохвугольніка.

Гл. таксама

• Упісаная акружнасць
• Прыўпісаная акружнасць