Функцыя размеркавання

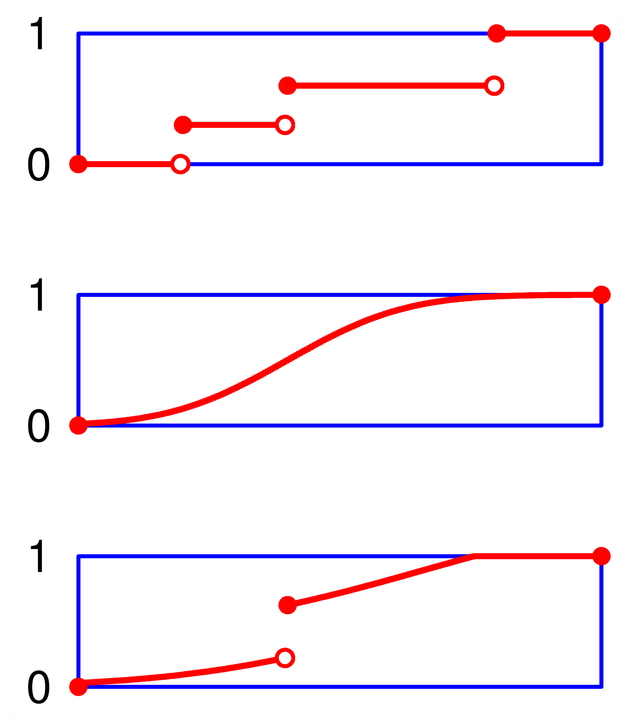
Функцыя размеркавання выпадковай велічыні — гэта функцыя, якая апісвае імавернасць таго, што выпадковая велічыня прыме значэнне, меншае за некаторы рэчаісны лік. Функцыя размеркавання задае размеркаванне выпадковай велічыні.

Прыклады непарыўных справа функцый размеркавання. У выпадку вызначэння функцый як непарыўных злева, выкалатыя і зафарбаваныя пункты ў месцах разрыву будуць памяняныя месцамі.

Азначэнне

Функцыяй размеркавання выпадковай велічыні завецца функцыя ${\displaystyle F_{\xi }:\mathbb {R} \to \mathbb {R} }$, якая вызначаецца праз роўнасць^[1]:70 $${\displaystyle F_{\xi }(x):=P(\xi <x),\forall x\in \mathbb {R} .}$$

У некаторых крыніцах функцыя размеркавання вызначаецца з іншым знакам: $${\displaystyle F_{\xi }(x):=P(\xi \leq x),\forall x\in \mathbb {R} .}$$ Такое вызначэнне ўплывае на ўласцівасць непарыўнасці, робячы функцыю непарыўнай справа, а не злева (гл. § Уласцівасці).

Існуе таксама абагульненне гэтага азначэння на многавымерныя выпадковыя велічыні.

Уласцівасці

Для функцыі размеркавання ${\displaystyle F}$ кожнай выпадковай велічыні ${\displaystyle \xi }$ справядлівыя наступныя ўласцівасці^[1]:71-74:

1. Манатоннасць^[en]. Калі ${\displaystyle x_{1}\leq x_{2}}$, то ${\displaystyle F(x_{1})\leq F(x_{2})}$.
2. Абмежаванасць^[en]. Маюць месца няроўнасці ${\displaystyle 0\leq F(x)\leq 1}$, прычым $${\displaystyle \lim _{x\to -\infty }F(x)=0,}$$$${\displaystyle \lim _{x\to +\infty }F(x)=1;}$$
3. Непарыўнасць злева. Для кожнага ${\displaystyle x_{0}\in \mathbb {R} }$ выконваецца $${\displaystyle \lim _{x\to x_{0}^{-}}F(x)=F(x_{0}).}$$

Для кожнай функцыі ${\displaystyle F:\mathbb {R} \to [0,1]}$, якая адпавядае ўмовам манатоннасці, абмежаванасці і непарыўнасці злева, існуюць імавернасная прастора ${\displaystyle (\Omega ,{\mathcal {A}},P)}$ і выпадковая велічыня ${\displaystyle \xi$ :\Omega \to \mathbb {R} } , у якой функцыя размеркавання ${\displaystyle F_{\xi }}$ супадае з ${\displaystyle F}$. Іншымі словамі, кожная такая функцыя і ёсць функцыяй размеркавання для некаторай выпадковай велічыні.

Часта функцыя размеркавання задаецца праз роўнасць ${\displaystyle F_{\xi }(x):=P(\xi \leq x),\forall x\in \mathbb {R} }$. У такім выпадку для яе характэрна ўласцівасць непарыўнасці справа, а не злева.

Доказы ўласцівасцей

Доказ манатоннасці

Няхай ${\displaystyle x_{1}\leq x_{2}}$. Тады ${\displaystyle (-\infty ,x_{1})\subset (-\infty ,x_{2})}$, і таму $${\displaystyle \xi ^{-1}(-\infty ,x_{1})\subset \xi ^{-1}(-\infty ,x_{2}),}$$ гэта значыць ${\displaystyle (\xi <x_{1})\subset (\xi <x_{2})}$.

Карыстаючыся манатоннасцю імавернасці, атрымліваем $${\displaystyle F(x_{1})=P(\xi <x_{1})\leq P(\xi <x_{2})=F(x_{2}).}$$

Доказ абмежаванасці

Няроўнасць ${\displaystyle 0\leq F(x)\leq 1}$ відавочна вынікае з ${\displaystyle 0\leq P(\xi <x)\leq 1}$.

Разгледзім улучэнні ${\displaystyle (-\infty ,-1)\supset (-\infty ,-2)\supset \dots \,}$. Заўважым, што ${\displaystyle \bigcap _{n=1}^{\infty }(-\infty ,-n)=\varnothing }$. Акрамя таго, $${\displaystyle \xi ^{-1}(-\infty ,-1)\supset \xi ^{-1}(-\infty ,-2)\supset \dots ,}$$ $${\displaystyle \bigcap _{n=1}^{\infty }\xi ^{-1}(-\infty ,-n)=\xi ^{-1}\left(\bigcap _{n=1}^{\infty }(-\infty ,-n)\right)=\xi ^{-1}(\varnothing )=\varnothing .}$$ Па аксіёме непарыўнасці імавернасці атрымліваем $${\displaystyle \lim _{n\to -\infty }F(n)=\lim _{n\to +\infty }P(\xi ^{-1}(-\infty ,-n))=0}$$ для ${\displaystyle n\in \mathbb {Z} }$. Няхай цяпер ${\displaystyle x\in \mathbb {R} }$ імкнецца да ${\displaystyle -\infty }$. З манатоннасці функцыі размеркавання вынікае ${\displaystyle F([x])\leq F(x)\leq F([x]+1).}$ Калі ${\displaystyle x\to -\infty }$, абедзве крайнія часткі няроўнасці імкнуцца да нуля. Карыстаючыся тэарэмай аб заціснутай функцыі^[en], атрымліваем $${\displaystyle \lim _{x\to -\infty }F(x)=0.}$$

Прадставім ${\displaystyle \mathbb {R} }$ як суму ${\displaystyle (-\infty ,0)+[0,1)+[1,2)+\dots }$ і, скарыстаўшы злічоную адытыўнасць, атрымаем $${\displaystyle 1=P_{\xi }(\mathbb {R} )=P_{\xi }((-\infty ,0))+\sum _{k=0}^{+\infty }P_{\xi }([k,k+1))=}$$ $${\displaystyle =\lim _{n\to +\infty }\left(P_{\xi }((-\infty ,0))+\sum _{k=0}^{n-1}P_{\xi }([k,k+1))\right)=}$$ $${\displaystyle =\lim _{n\to +\infty }P_{\xi }((-\infty ,0)+[0,1)+[1,2)+\dots +[n-1,n))=}$$ $${\displaystyle =\lim _{n\to +\infty }P_{\xi }((-\infty ,n))=\lim _{n\to +\infty }F(n)}$$ для ${\displaystyle n\in \mathbb {Z} }$. Доказ для ${\displaystyle x\in \mathbb {R} }$ праводзіцца аналагічна папярэдняму выпадку праз тэарэму аб заціснутай функцыі.

Доказ непарыўнасці злева

Возьмем адвольную нарастальную паслядоўнасць рэчаісных лікаў ${\displaystyle (x_{n})_{n=1}^{\infty }}$, якая збягаецца да ${\displaystyle x_{0}}$. Існаванне ліміту^[en] ${\displaystyle \lim _{x\to x_{0}^{-}}F(x)}$ вынікае з манатоннасці ${\displaystyle F}$. Пакажам, што гэты ліміт роўны ${\displaystyle F(x_{0})}$.

Заўважым, што ${\displaystyle \varnothing =\bigcup _{n=1}^{\infty }[x_{n},x_{0})}$ і ${\displaystyle [x_{n},x_{0})\supset [x_{n+1},x_{0})\,\forall n\in \mathbb {N} }$. Карыстаючыся аксіёмамі непарыўнасці і адытыўнасцю імавернасці, атрымліваем

${\displaystyle 0=\lim _{n\to +\infty }P_{\xi }([x_{n},x_{0}))=\lim _{n\to +\infty }P_{\xi }((-\infty ,x_{0})\setminus ((-\infty ,x_{n}))=}$
${\displaystyle =\lim _{n\to +\infty }(P_{\xi }((-\infty ,x_{0}))-P_{\xi }((-\infty ,x_{n})))=}$
${\displaystyle =F(x_{0})-\lim _{x_{n}\to x_{0}}F(x_{n}).}$
Адсюль вынікае ${\displaystyle \lim _{x\to x_{0}^{-}}F(x)=F(x_{0})}$.

Гл. таксама

• Умоўная функцыя размеркавання
• Функцыя імавернасці
• Шчыльнасць імавернасці

Зноскі

1. Звяровіч Э. І., Радына А. Я. Элементы тэорыі імавернасцей. — Мінск: Беларусь, 2013. — ISBN 978-985-01-1043-5.