Векторно произведение

Векторното произведение на два вектора ${\displaystyle \mathbf {a} }$ и ${\displaystyle \mathbf {b} }$ е вектор, перпендикулярен на равнината, определена от векторите ${\displaystyle \mathbf {a} }$ и ${\displaystyle \mathbf {b} }$, образува дясна тройка с тях и има дължина, равна на произведението от големините на двата вектора и синуса на ъгъла между тях.

Ъгълът между два вектора приема стойности от ${\displaystyle 0^{\circ }}$ до ${\displaystyle 180^{\circ }}$, следователно синусът му, а оттам – и дължината на векторното произведение са неотрицателни (т.е. дължината е коректно дефинирана):

${\displaystyle \Vert \mathbf {a} \times \mathbf {b} \Vert =\Vert \mathbf {a} \Vert \Vert \mathbf {b} \Vert \sin \sphericalangle (\mathbf {a}$ ;\ \mathbf {b} )}

Самото векторно произведение на два вектора се дефинира така:

${\displaystyle \mathbf {a} \times \mathbf {b} =\Vert \mathbf {a} \Vert \Vert \mathbf {b} \Vert \sin \sphericalangle (\mathbf {a}$ ;\ \mathbf {b} )\ \mathbf {\hat {n}} }

като тук ${\displaystyle \mathbf {\hat {n}} ={\frac {\mathbf {a} \times \mathbf {b} }{\Vert \mathbf {a} \times \mathbf {b} \Vert }}}$.

Векторното произведение на ${\displaystyle \mathbf {a} }$ и ${\displaystyle \mathbf {b} }$

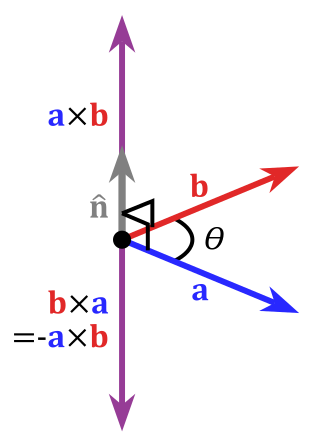
Ако са нанесени векторите ${\displaystyle \mathbf {a} }$ и ${\displaystyle \mathbf {b} }$ с общо начало, то директрисата на вектора ${\displaystyle (\mathbf {a} \times \mathbf {b} )}$ минава през това начало и е перпендикулярна на равнината, образувана от ${\displaystyle \mathbf {a} }$ и ${\displaystyle \mathbf {b} }$. Посоката на вектора се определя с правилото ${\displaystyle (\mathbf {a} ,\mathbf {b} ,\mathbf {a} \times \mathbf {b} )}$ да образуват дясно ориентирана тройка вектори.

Аналитично представяне

Ако векторите ${\displaystyle \mathbf {a} }$ и ${\displaystyle \mathbf {b} }$ са зададени с координатите си ${\displaystyle \mathbf {a} =(a_{1},a_{2},a_{3})}$ и ${\displaystyle \mathbf {b} =(b_{1},b_{2},b_{3})}$ в тримерното пространство и ${\displaystyle \mathbf {i} ,\mathbf {j} ,\mathbf {k} }$ са единичните вектори на дясно ориентирана ортонормирана координатна система, то:

${\displaystyle \mathbf {a} \times \mathbf {b} =\mathrm {det} \left({\begin{matrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\end{matrix}}\right)}$.

По-подробно горната формула изглежда така: ${\displaystyle {\begin{aligned}\mathbf {a} \times \mathbf {b} &=\mathbf {i} \ \mathrm {det} \left({\begin{matrix}a_{2}&a_{3}\\b_{2}&b_{3}\end{matrix}}\right)-\mathbf {j} \ \mathrm {det} \left({\begin{matrix}a_{1}&a_{3}\\b_{1}&b_{3}\end{matrix}}\right)+\mathbf {k} \ \mathrm {det} \left({\begin{matrix}a_{1}&a_{2}\\b_{1}&b_{2}\end{matrix}}\right)\\&=\mathbf {i} (a_{2}b_{3}-a_{3}b_{2})-\mathbf {j} (a_{1}b_{3}-a_{3}b_{1})+\mathbf {k} (a_{1}b_{2}-a_{2}b_{1})\end{aligned}}}$

Свойства

• Антикомутативност: ${\displaystyle \mathbf {a} \times \mathbf {b} =-\mathbf {b} \times \mathbf {a} }$

Доказателство:

${\displaystyle {\begin{aligned}\mathbf {a} \times \mathbf {b} &=\mathrm {det} \left({\begin{matrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\end{matrix}}\right)\\&=-\mathrm {det} \left({\begin{matrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\b_{1}&b_{2}&b_{3}\\a_{1}&a_{2}&a_{3}\end{matrix}}\right)\\&=-\mathbf {b} \times \mathbf {a} \end{aligned}}}$

• Дистрибутивност: ${\displaystyle (\mathbf {a} +\mathbf {b} )\times \mathbf {c} =\mathbf {a} \times \mathbf {c} +\mathbf {b} \times \mathbf {c} }$

Доказателство:

Тъй като ${\displaystyle \mathbf {a} +\mathbf {b} =(a_{1}+b_{1},\ a_{2}+b_{2},\ a_{3}+b_{3})}$, то:

${\displaystyle {\begin{aligned}(\mathbf {a} +\mathbf {b} )\times \mathbf {c} &=\mathrm {det} \left({\begin{matrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\{a_{1}+b_{1}}&{a_{2}+b_{2}}&{a_{3}+b_{3}}\\c_{1}&c_{2}&c_{3}\end{matrix}}\right)\\&=\mathrm {det} \left({\begin{matrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\a_{1}&a_{2}&a_{3}\\c_{1}&c_{2}&c_{3}\end{matrix}}\right)+\mathrm {det} \left({\begin{matrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\b_{1}&b_{2}&b_{3}\\c_{1}&c_{2}&c_{3}\end{matrix}}\right)\\&=\mathbf {a} \times \mathbf {c} +\mathbf {b} \times \mathbf {c} \end{aligned}}}$

• Линейност: ${\displaystyle (\lambda \mathbf {a} )\times (\mu \mathbf {b} )=\lambda \mu (\mathbf {a} \times \mathbf {b} )}$ за произволни реални числа ${\displaystyle \lambda }$ и ${\displaystyle \mu }$.

Доказателство:

Понеже ${\displaystyle \lambda \mathbf {a} =(\lambda a_{1},\ \lambda a_{2},\ \lambda a_{3})}$ и ${\displaystyle \mu \mathbf {b} =(\mu b_{1},\ \mu b_{2},\ \mu b_{3})}$, то:

${\displaystyle {\begin{aligned}(\lambda \mathbf {a} )\times (\mu \mathbf {b} )&=\mathrm {det} \left({\begin{matrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\\lambda a_{1}&\lambda a_{2}&\lambda a_{3}\\\mu b_{1}&\mu b_{2}&\mu b_{3}\end{matrix}}\right)\\&=\lambda \mu \ \mathrm {det} \left({\begin{matrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\end{matrix}}\right)\\&=\lambda \mu (\mathbf {a} \times \mathbf {b} )\end{aligned}}}$

• Ако ${\displaystyle \mathbf {a} \parallel \mathbf {b} }$, то ${\displaystyle \mathbf {a} \times \mathbf {b} =\mathbf {0} }$

Доказателство:

Щом ${\displaystyle \mathbf {a} \parallel \mathbf {b} }$, то ${\displaystyle \sphericalangle (\mathbf {a} ,\ \mathbf {b} )=0^{\circ }}$, откъдето следва, че

${\displaystyle \mathbf {a} \times \mathbf {b} =\Vert \mathbf {a} \Vert \Vert \mathbf {b} \Vert \sin 0^{\circ }\ \mathbf {\hat {n}} =\mathbf {0} }$

Пресмятане на векторното произведение

Нека ${\displaystyle \mathbf {i} ,\mathbf {j} ,\mathbf {k} }$ са единичните вектори на дясно ориентирана ортонормирана координатна система. Тогава са в сила равенствата:

${\displaystyle {\begin{aligned}{\boldsymbol {\mathrm {i} }}\times {\boldsymbol {\mathrm {j} }}={\boldsymbol {\mathrm {k} }}\\{\boldsymbol {\mathrm {j} }}\times {\boldsymbol {\mathrm {k} }}={\boldsymbol {\mathrm {i} }}\\{\boldsymbol {\mathrm {k} }}\times {\boldsymbol {\mathrm {i} }}={\boldsymbol {\mathrm {j} }}\end{aligned}}}$.

Понеже векторното произведение е антикомутативно, то:

${\displaystyle {\begin{aligned}{\boldsymbol {\mathrm {j} }}\times {\boldsymbol {\mathrm {i} }}=-{\boldsymbol {\mathrm {k} }}\\{\boldsymbol {\mathrm {k} }}\times {\boldsymbol {\mathrm {j} }}=-{\boldsymbol {\mathrm {i} }}\\{\boldsymbol {\mathrm {i} }}\times {\boldsymbol {\mathrm {k} }}=-{\boldsymbol {\mathrm {j} }}\end{aligned}}}$.

Освен това лесно може да се покаже, че ${\displaystyle \mathbf {i} \times \mathbf {i} =\mathbf {j} \times \mathbf {j} =\mathbf {k} \times \mathbf {k} =\mathbf {0} }$ (равенствата следват от антикомутативността на векторното произведение).

С помощта на тези равенства можем да изразим векторното произведение на векторите ${\displaystyle \mathbf {a} }$ и ${\displaystyle \mathbf {b} }$.

Понеже

${\displaystyle {\begin{alignedat}{3}\mathbf {a} &=a_{1}\mathbf {i} &&+a_{2}\mathbf {j} &&+a_{3}\mathbf {k} \\\mathbf {b} &=b_{1}\mathbf {i} &&+b_{2}\mathbf {j} &&+b_{3}\mathbf {k} \end{alignedat}}}$

то векторното произведение ${\displaystyle \mathbf {a} \times \mathbf {b} }$ ще бъде равно на:

${\displaystyle {\begin{aligned}\mathbf {a} \times \mathbf {b} ={}&(a_{1}\mathbf {i} +a_{2}\mathbf {j} +a_{3}\mathbf {k} )\times (b_{1}\mathbf {i} +b_{2}\mathbf {j} +b_{3}\mathbf {k} )\\={}&a_{1}b_{1}(\mathbf {i} \times \mathbf {i} )+a_{1}b_{2}(\mathbf {i} \times \mathbf {j} )+a_{1}b_{3}(\mathbf {i} \times \mathbf {k} )+{}\\&a_{2}b_{1}(\mathbf {j} \times \mathbf {i} )+a_{2}b_{2}(\mathbf {j} \times \mathbf {j} )+a_{2}b_{3}(\mathbf {j} \times \mathbf {k} )+{}\\&a_{3}b_{1}(\mathbf {k} \times \mathbf {i} )+a_{3}b_{2}(\mathbf {k} \times \mathbf {j} )+a_{3}b_{3}(\mathbf {k} \times \mathbf {k} )\\={}&\ a_{1}b_{1}\mathbf {0} +a_{1}b_{2}\mathbf {k} -a_{1}b_{3}\mathbf {j} \ -\\&a_{2}b_{1}\mathbf {k} +a_{2}b_{2}\mathbf {0} +a_{2}b_{3}\mathbf {i} \ +\\&a_{3}b_{1}\mathbf {j} \ -a_{3}b_{2}\mathbf {i} \ +a_{3}b_{3}\mathbf {0} \\={}&(a_{2}b_{3}-a_{3}b_{2})\mathbf {i} +(a_{3}b_{1}-a_{1}b_{3})\mathbf {j} +(a_{1}b_{2}-a_{2}b_{1})\mathbf {k} \\\end{aligned}}}$

Геометрично тълкуване

Нека с ${\displaystyle S}$ бележим лицето на успоредника и нека ${\displaystyle \theta }$ е ъгълът, заключен между ${\displaystyle \mathbf {a} }$ и ${\displaystyle \mathbf {b} }$. Тогава:

${\displaystyle S=\Vert \mathbf {a} \Vert \Vert \mathbf {b} \Vert \sin \theta =\Vert \mathbf {a} \times \mathbf {b} \Vert }$

Приложение

• В аналитичната геометрия: Пресмятане на лице на успоредник и лице на триъгълник;
• В механиката: пресмятане на момент на сила, въртящ момент;
• В механиката на непрекъснатите среди (електро -, аеро – и хидродинамика): пресмятане на ротацията на векторно поле.