Геометрична прогресия

Геометрѝчна прогрèсия в математиката е редица от числа, в която първото число е различно от нула, а всяко следващо число е получено от предишното чрез умножение с константа, различна от нула. Тази константа се нарича частно, а числата – членове на прогресията.

За всяка геометрична прогресия ${\displaystyle a_{1},\,a_{2},\,...,\,a_{n},\,...}$ е в сила равенството ${\displaystyle a_{n}=a_{n-1}q}$, където ${\displaystyle a_{1}\neq 0}$, ${\displaystyle q\neq 0}$ е частното на прогресията, ${\displaystyle n\in \mathbb {N} ,n\geqslant 2.}$^[1] Очевидно една геометрична прогресия е напълно определена, ако се знаят първия ѝ член и нейното частно. В този смисъл тя е рекурсивна редица.

Например редицата 2, 4, 8, 16, 32, ... е геометрична прогресия с първи член 2 и частно 2, а геометричната прогресия 40, 20, 10, 5, ... е с първи член 20 и частно 1/2. Първата е пример за нарастваща, а втората – за намаляваща прогресия.

Диаграма, илюстрираща три основни геометрични прогресии от модела 1(rⁿ⁻¹) до 6 повторения в дълбочина. Първият блок е единичен блок, а пунктираната линия представлява безкрайна сума на прогресията – число, към което тя ще се приближава, но никога няма да го достигне: 2, 3/2, и 4/3 съответно.^[2]

Конструиране на триъгълника на Серпински. Това е фрактал. Броят на черните триъгълници, дължината на страната им, индивидуалната им площ и площта на покритата област следват геометрични прогресии със съответни съотношения 3, 1/2, 1/4, 3/4.

Геометричната прогресия е известна още с имената геометрична редица (от английски geometric sequence) и кратна прогресия (от руски кратная прогрессия).

Формули за общия член и частното

Формулата за ${\displaystyle n}$-тия член на прогресията е рекурентното съотношение ${\displaystyle a_{n}=a_{1}q^{n-1}}$.
Получава се като се изразява всеки член чрез определението за геометрична прогресия и се прилага методът на математичната индукция за ${\displaystyle n}$-тия член:

${\displaystyle {\begin{aligned}a_{2}&=a_{1}q\\a_{3}&=a_{2}q=(a_{1}q)\cdot q=a_{1}q^{2}\\a_{4}&=a_{3}q=(a_{1}q^{2})\cdot q=a_{1}q^{3}\\&\vdots \\a_{n}&=a_{n-1}q=(a_{1}q^{n-2})\cdot q=a_{1}q^{n-1}\\\end{aligned}}}$

Обобщена формула за общия член:

${\displaystyle a_{n}=a_{k}\cdot q^{n-k},}$ където ${\displaystyle k<n;\;\forall n,\forall k\in \mathbb {N} .}$

Формулите за частното следват от определението за геометрична прогресия: ${\displaystyle q={\frac {a_{n}}{a_{n-1}}}={\frac {a_{n+1}}{a_{n}}}}$;

${\displaystyle q={\sqrt[{n-k}]{\dfrac {a_{n}}{a_{k}}}},}$ където ${\displaystyle k<n;\;\forall n,\forall k\in \mathbb {N} .}$

Тук трябва да се приеме ${\displaystyle q\neq 0}$, тъй като в противен случай съотношението ${\displaystyle {\tfrac {a_{n+1}}{a_{n}}}}$ не би съществувало за всички съседни членове.^{[Бел. 1]}

Анализ на частното

• ${\displaystyle q>1:}$ клоняща към плюс или минус безкрайност редица в зависимост от знака на първия член
  (напр. 1, 3, 9, 27, ... ${\displaystyle \to +\infty }$ или -1, -4, -16, -64, ... ${\displaystyle \to -\infty }$);
• ${\displaystyle 0<q<1:}$ редицата клони към ${\displaystyle 0}$ (напр. прогресиите ${\textstyle +5,\ 1,\ {\frac {1}{5}},\ {\frac {1}{25}},\ {\frac {1}{125}},\ \dotsc \to 0}$ или ${\textstyle -4,\ -1,\ -{\frac {1}{4}},\ -{\frac {1}{16}},\ {\frac {1}{64}},\ \dotsc \to 0}$;
• ${\displaystyle q<0:}$ ще се получи редуване на положителни и отрицателни числа;
• ${\displaystyle -1<q<0:}$ редицата клони към нула с редуващи се положителни и отрицателни членове:

${\textstyle +1,\ -{\frac {1}{2}},\ +{\frac {1}{4}},\ -{\frac {1}{8}},\ +{\frac {1}{16}},\ -{\frac {1}{32}},\ +{\frac {1}{64}},\ -{\frac {1}{128}},\ +{\frac {1}{256}},\ \dotsc \to 0}$.
Като цяло, ${\textstyle a_{n}=1\cdot \left(-{\frac {1}{2}}\right)^{n}=(-1)^{n}/2^{n}}$;

• ${\displaystyle q<-1:}$ могат да се разглеждат 2 редици: нечетните номера клонят към плюс безкрайност, а четните – към минус безкрайност, или обратно в зависимост от знака на първия член. Например при ${\displaystyle q=-3:}$ прогресията 2, -6, 18, -54, 162, -486, ... е съставена от редиците 2, 18, 162, ... ${\displaystyle \to +\infty }$ и
  -6, -54, -486, ... ${\displaystyle \to -\infty }$ или прогресията -1, 3, -9, 27, -81, 243, ... е съставена от редиците
  -1, -9, -81, ... ${\displaystyle \to -\infty }$ и 3, 27, 243, ... ${\displaystyle \to +\infty }$;
• ${\displaystyle q=1:}$ редицата е съставена от константи, равни на първия член (${\displaystyle 6,6,...,6}$);
• ${\displaystyle q=-1:}$ редицата е съставена от константи, равни или противоположни на първия член, в зависимост от четността на поредния номер (напр. −π, π, −π, π, ...);
• ${\displaystyle q=0:}$ редицата се състои само от нули, с изключение на първия член.

Сходимост на геометричните прогресии

В изследването на границата на безкрайна геометрична последователност ${\displaystyle (a_{1}q^{n})}$ трябва да се разграничават различните случаи: За ${\displaystyle a_{1}=0}$ постоянната последователност ${\displaystyle 0,0,\ldots }$ е сходяща и равна на нула. За ${\displaystyle a_{1}\neq 0}$ сходимостта зависи от частното ${\displaystyle q}$:

Случай 1: За ${\displaystyle q=-1}$ следващите членове винаги се изменят скокообразно напред-назад между ${\displaystyle a_{1}}$ и ${\displaystyle -a_{1}}$, така че геометричната прогресия е разходяща.

Случай 2: За ${\displaystyle q=1}$ постоянната последователност ${\displaystyle a_{1},a_{1},\ldots ,}$ е сходяща и равна на ${\displaystyle a_{1}}$.

Случай 3: За ${\displaystyle |q|>1}$ всеки следващ член ${\displaystyle a_{n+1}=a_{n}\cdot q}$ е по-голям от предишния ${\displaystyle a_{n+1}>a_{n}}$ при ${\displaystyle q>1}$ и по-малък от него ${\displaystyle a_{n+1}<a_{n}}$ при ${\displaystyle q<-1}$. В обобщение ${\displaystyle |a_{n+1}|>|a_{n}|}$ и прогресията е разходяща.

Случай 4: За ${\displaystyle |q|<1}$ се получава ${\displaystyle {\frac {1}{|q|}}>1,}$ така
${\displaystyle (1)\,\,\,\,{\frac {1}{|q|}}=1+\delta \,}$ за ${\displaystyle \delta >0.}$

Сега, ако ${\displaystyle \varepsilon >0,}$ тогава според аксиомата на Архимед съществува ${\displaystyle N\in \mathbb {N} ,}$ така че

${\displaystyle (2)\,\,\,\,n\delta >1/\varepsilon \,}$ за всички ${\displaystyle n>N.}$

От (1) и (2), заедно с неравенството на Бернули, следва:

${\displaystyle \left(1/|q|\right)^{n}=(1+\delta )^{n}\geq 1+n\delta \geq n\delta >1/\varepsilon \,}$ за всички ${\displaystyle n>N.}$

Така ${\displaystyle |q^{n}|=|q|^{n}<\varepsilon }$ за всички ${\displaystyle n>N.}$

Това означава, че ${\displaystyle (q^{n})}$ е нулева редица. Но тогава и ${\displaystyle (a_{1}q^{n})}$ също се стреми към нула и прогресията е сходяща.

Видове геометрични прогресии

Геометричните прогресии не се делят на различни видове като отделни категории, а се класифицират по своята монотонност според характеристиките на техните членове и частното ${\displaystyle q}$, което е отношение на последователни членове. Ако всеки член на геометричната прогресия е по-голям от предишния, тогава прогресията се нарича „нарастваща“; ако е по-малък от предишния, тогава тя се нарича „намаляваща“.^[3]

Нарастващи

Геометричната прогресия е нарастваща или растяща, ако се изпълнява един из наборите условия:

${\displaystyle a_{1}>0\quad }$ и ${\displaystyle \quad q>1\quad }$ (напр. 2, 4, 8, 16, ... ; q = 2) – всички членове са положителни и нарастват

или

${\displaystyle a_{1}<0\quad }$ и ${\displaystyle \quad 0<q<1\quad }$ (напр. -81, -27, -9, -3, ... ; q = -3) – всички членове са отрицателни и нарастват.

Такава прогресия се нарича още монотонно растяща.

Намаляващи

Геометричната прогресия е намаляваща, ако се изпълнява един от наборите условия:

${\displaystyle a_{1}>0\quad }$ и ${\displaystyle \quad 0<q<1}$ (напр. 24, 8, 3, 1/3, ... ; q=1/3) – всички членове са положителни и намаляват

или

${\displaystyle a_{1}<0\quad }$ и ${\displaystyle \quad q>1}$ (напр. -1/32, -1/16, -1/8, -1/4, ... ; q=2) – всички членове са отрицателни и намаляват.

Такава прогресия се нарича още монотонно намаляваща.

Доказателство за нарастващи и намаляващи геометрични прогресии: Записва се разликата между ${\displaystyle \left(n+1\right)}$-ия и ${\displaystyle n}$-ия член на геометричната прогресия по формулата за общия член:

${\displaystyle a_{n+1}-a_{n}=a_{1}\cdot q^{n-1}\cdot \left(q-1\right).}$

За нарастваща прогресия тази разлика трябва да е положителна, независимо от номера ${\displaystyle n}$, а за намаляваща – отрицателна. Условията, записани в доказаното твърдение, гарантират, че разликата между членовете ${\displaystyle a_{n+1}}$ и ${\displaystyle a_{n}}$ ще имат определен знак.

Постоянни (стационарни)

Частният случай, при който отношението q = 1. Всички членове са еднакви и равни на първия член (напр. 5, 5, 5, 5, ...).

Знакоредуващи се (алтернативни)^[4]

Частният случай, при който отношението q < 0. Членовете редуват знаците си, а прогресията е нито растяща, нито намаляваща.

При ${\displaystyle a_{1}>0}$:

• ако ${\displaystyle 0>q>-1}$ (напр. ${\textstyle 3,\ -1,\ +{\frac {1}{3}},\ -{\frac {1}{9}},\ +{\frac {1}{27}},\ -{\frac {1}{81}},\ \dotsc$ ;\quad q=-{\frac {1}{3}}} ), нечетните членове образуват намаляваща, а четните – растяща геометрична прогресия.
• ако ${\displaystyle q<-1}$ (напр. ${\displaystyle 2,\ -4,\ 8,\ -16,\ 32,\ -64,\ ...;\quad q=-2}$), нечетните членове образуват растяща, а четните – намаляваща геометрична прогресия.
  

При ${\displaystyle a_{1}<0}$:

• ако ${\displaystyle 0>q>-1}$ (напр. ${\textstyle -{\frac {5}{3}},\ +{\frac {5}{6}},\ -{\frac {5}{12}},\ +{\frac {5}{24}},\ -{\frac {5}{48}},\ +{\frac {5}{96}},\ \dotsc$ ;\quad q=-{\frac {1}{2}}} ), нечетните членове образуват растяща, а четните – намаляваща геометрична прогресия.
• ако ${\displaystyle q<-1}$ (напр. ${\displaystyle -1,\ 5,\ -25,\ 125,\ ...;\quad q=-5}$), нечетните членове образуват намаляваща, а четните – растяща геометрична прогресия.

Видове геометрични прогресии

${\displaystyle a_{1}>0}$	${\displaystyle q>1}$	нарастваща
	${\displaystyle 0<q<1}$	намаляваща
${\displaystyle a_{1}<0}$	${\displaystyle q>1}$	намаляваща
	${\displaystyle 0<q<1}$	нарастваща
	${\displaystyle q=1}$	постоянна
	${\displaystyle q<0}$	знакоредуваща се

Свойства

• Всеки член на геометричната прогресия след първия е средно геометричен на съседните си членове, т. е. ${\displaystyle a_{n}^{2}=a_{n-1}a_{n+1}}$ за всяко ${\displaystyle n\geq 2}$. От тук идва името геометрична прогресия:

${\displaystyle a_{n-1}\cdot a_{n+1}=a_{1}q^{n-1}\cdot a_{1}q^{n+1}=a_{1}^{2}q^{2n}=(a_{1}q^{n})^{2}=a_{n}^{2}}$,

откъдето

${\displaystyle a_{n}={\sqrt {a_{n-1}\cdot a_{n+1}}}.}$

Може да се докаже и по обратния път:

${\displaystyle a_{n}^{2}=a_{n}a_{n}=a_{1}q^{n-1}a_{1}q^{n-1}=a_{1}q^{n-1-i}a_{1}q^{n-1+i}=a_{n-i}a_{n+i}.}$

По-точна е следната формулировка на характеристичното свойство: Модулът на всеки член на геометрична прогресия, с изключение на първия, е равен на средната геометрична стойност (пропорционална средна стойност) на двата члена до него^{[Бел. 2]}

${\displaystyle |a_{n}|={\sqrt {a_{n-1}a_{n+1}}},}$

• В сила е и обратното твърдение, което е признак за геометрична прогресия: ако ${\displaystyle a_{1},\,a_{2},\,...,\,a_{n},\,...}$ е числова редица с ненулеви членове, в която всеки член след първия е средно геометричен на съседните си членове, то тази редица е геометрична прогресия.
  

Даденият признак може да се разшири за други случаи.
Ако членовете на геометричната прогресия са отрицателни, се получава ${\displaystyle a_{n}=-{\sqrt {a_{n-1}\cdot a_{n+1}}}}$, където ${\displaystyle n\geqslant 2}$.

Ако знаците на членовете на прогресията се редуват, получаваме ${\displaystyle a_{n}=\left(-1\right)^{n+j}{\sqrt {a_{n-1}\cdot a_{n+1}}}}$, където ${\displaystyle j=0}$ или ${\displaystyle j=1}$ и ${\displaystyle n\geqslant 2}$.

• Нека ${\displaystyle a_{k},a_{l},a_{m}}$ са съответно ${\displaystyle k}$-ти, ${\displaystyle l}$-ти и ${\displaystyle m}$-ти членове на геометрична прогресия, където ${\displaystyle k,\,l,\,m\in \mathbb {N} }$. Тогава за всяка такава тройка е валидно допълнителното свойство на геометрична прогресия, наречено тъждество на геометрична прогресия:

${\displaystyle a_{k}^{l-m}\cdot a_{l}^{m-k}\cdot a_{m}^{k-l}=1.}$

• Логаритмите на членовете на геометрична прогресия образуват аритметична прогресия.

${\displaystyle \log(a_{n})=\log(a_{1}q^{n-1})=\log(a_{1})+(n-1)\cdot \log(q)}$

Формула за общия член на аритметична прогресия: ${\displaystyle b_{n}=b_{1}+(n-1)\cdot d}$.
В нашия случай ${\displaystyle b_{1}=\log(a_{1})}$, ${\displaystyle d=\log(q)}$.

Графична интерпретация

Ако нанесем точки с координати ${\displaystyle \left(n;\,a_{n}\right)}$ върху координатна равнина, където ${\displaystyle n}$ е естествено число и ${\displaystyle a_{n}}$ е ${\displaystyle n}$-тият член на някаква геометрична прогресия, за която ${\displaystyle q>0}$, тогава всички точки ще принадлежат на графиката на функцията

${\displaystyle y=a_{1}\cdot q^{x-1}={\frac {a_{1}}{q}}\cdot q^{x},}$

където ${\displaystyle q}$ е частното на геометричната прогресия, а ${\displaystyle a_{1}}$ е първият ѝ член.^[3] Това означава, че е валидна следната теорема:

За да бъде една редица ${\displaystyle \left\{a_{n}\right\}}$ геометрична прогресия за ${\displaystyle q>0}$, е необходимо и достатъчно ${\displaystyle a_{n}}$ да е експоненциална функция (на ${\displaystyle n}$), дефинирана върху множеството от естествени числа.^[3]

Примери

Получаване на нови квадрати чрез свързване на средните точки на страните на предишни квадрати

• Последователността от квадратни площи, където всеки следващ квадрат се получава чрез съединяване на средните точки на страните на предишния, е безкрайна геометрична прогресия с частно 1/2. Площите на триъгълниците, получени на всяка стъпка, също образуват безкрайна геометрична прогресия със знаменател 1/2, чийто сбор е равен на площта на началния квадрат.^{[2]:с. 8 – 9}
• Последователността на броя на зърната в квадратите в задачата за зърната на шахматна дъска е геометрична прогресия.

Сума на геометрична прогресия

Визуално доказателство на формулата за сума на първите ${\displaystyle n}$ члена на геометрична прогресия.
Ако |r| < 1 и n → ∞, терминът rⁿ изчезва, оставяйки S_∞ = a1 − r

Сумата на първите ${\displaystyle n}$ члена на геометричната прогресия е

${\displaystyle S_{n}=a_{1}+a_{2}+a_{3}+\dots +a_{n}=\sum _{i=1}^{n}a_{i}}$

или, записана подробно,

${\displaystyle (3)\,\,\,S_{n}=a_{1}+a_{1}q+a_{1}q^{2}+a_{1}q^{3}+\dots +a_{1}q^{n-1}.}$

Умножаваме двете страни на (1) с частното ${\displaystyle q}$ и получаваме

${\displaystyle (4)\,\,\,qS_{n}=a_{1}q+a_{1}q^{2}+a_{1}q^{3}+a_{1}q^{4}+\dots +a_{1}q^{n}.}$

Изваждаме (4) от (3) и намираме

${\displaystyle (5)\,\,\,S_{n}-qS_{n}=a_{1}-a_{1}q^{n}\Rightarrow (1-q)S_{n}=a_{1}(1-q^{n}).}$

Оттук, ако ${\displaystyle q\neq 1}$, се получава формулата за сума на първите ${\displaystyle n}$ члена на геометрична прогресия:

${\displaystyle (6)\,\,\,S_{n}={a_{1}(1-q^{n}) \over (1-q)}.}$

Формулата е удобна ако ${\displaystyle q<1}$. При ${\displaystyle q>1}$ тя може да се изведе като се извади (3) от (4) и се получава във вида

${\displaystyle (7)\,\,\,S_{n}={a_{1}(q^{n}-1) \over (q-1)}.}$

В частност при ${\displaystyle q=1}$ имаме

${\displaystyle (8)\,\,\,S_{n}=a_{1}+a_{2}+\dots +a_{n}=\underbrace {a_{1}+a_{1}+\dots +a_{1}} _{n}=na_{1}.}$

Геометричен ред

Сумата на безкрайната геометрична прогресия
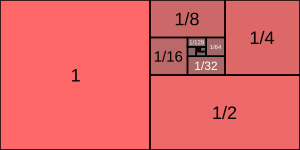
1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + ... клони към 2.

 Основна статия: Геометричен ред

Геометричният ред е сбор от безкраен брой членове, който има постоянно съотношение между последователните си членове

${\displaystyle (9)\,\,\,a+aq+aq^{2}+aq^{3}+\cdots =\sum _{n=0}^{\infty }aq^{n}}$.

Това е сума на безкрайна геометрична прогресия.

При ${\displaystyle a_{1}>0}$ и ${\displaystyle \left|q\right|<1}$ прогресията е намаляваща и нейната ${\displaystyle n}$-та (частична, парциална) сума се дава с (6). Ако имаме още, че ${\displaystyle n\to \infty }$, то е изпълнено ${\displaystyle q^{n}\to 0}$ и тогава под сума на прогресията се разбира границата

${\displaystyle (10)\,\,\,\lim _{n\to \infty }{S_{n}}=\lim _{n\to \infty }{\frac {a_{1}(1-q^{n})}{1-q}}={\frac {a_{1}}{1-q}}.}$

Равенството (10) е известно като сума на безкрайно намаляваща геометрична прогресия.

Свойства на сумата на геометрична прогресия

${\displaystyle a_{n+1}=S_{n+1}-S_{n};}$

${\displaystyle S_{n}=\sigma _{n}\cdot a_{1}a_{n},}$

където ${\displaystyle \sigma _{n}}$ е сумата от реципрочни числа, т.е. ${\displaystyle \sigma _{n}={\dfrac {1}{a_{1}}}+{\dfrac {1}{a_{2}}}+\cdots +{\dfrac {1}{a_{n-1}}}+{\dfrac {1}{a_{n}}}.}$

Произведение на геометрична прогресия

Произведението на първите ${\displaystyle n}$ члена на геометрична прогресия е

${\displaystyle P_{n}=a_{1}a_{2}a_{3}\cdot \cdot \cdot a_{n}=\prod _{k=1}^{n}a_{k}=a_{1}\cdot a_{1}q\cdot a_{1}q^{2}\cdots a_{1}q^{n-1}.}$

Оттук лесно получаваме, че ${\displaystyle P_{n}=a_{1}^{n}q^{1+2+3+\cdot \cdot \cdot +n-1}.}$

Сумата в степенния показател на ${\displaystyle q}$ е всъщност сума на аритметична прогресия с първи член ${\displaystyle b_{1}=1}$, разлика ${\displaystyle d=1}$ и последен член ${\displaystyle b_{n-1}=n-1}$ и е числено равна на ${\displaystyle {\frac {(n-1)n}{2}}={\frac {n^{2}-n}{2}}.}$ Така произведението на първите ${\displaystyle n}$ члена на геометрична прогресия (за която предполагаме, че са изпълнени условията ${\displaystyle a_{1}\neq 0,\,\,q\neq 0}$) се дава с формулата

${\displaystyle (10)\,\,\,P_{n}=a_{1}^{n}q^{\frac {n^{2}-n}{2}}.}$

Тя може да се преобразува във вида
${\displaystyle P_{n}=a_{1}^{n}q^{\frac {n^{2}-n}{2}}=a_{1}^{\frac {n}{2}}a_{1}^{\frac {n}{2}}q^{\frac {n(n-1)}{2}}=\left(a_{1}a_{1}q^{n-1}\right)^{\frac {n}{2}},\,\,\,}$ или окончателно

${\displaystyle (11)\,\,\,P_{n}=\left(a_{1}a_{n}\right)^{\frac {n}{2}}.}$

Произведението на членовете на геометрична прогресия, започвайки с ${\displaystyle k}$-тия член и завършвайки с ${\displaystyle n}$-тия член, може да се изчисли по формулата

${\displaystyle P_{k,n}={\dfrac {P_{n}}{P_{k-1}}}.}$

Доказателство:
${\displaystyle P_{k,n}=\prod _{i=k}^{n}a_{i}={\frac {\prod _{i=1}^{n}a_{i}}{\prod _{j=1}^{k-1}a_{j}}}={\frac {P_{n}}{P_{k-1}}}.}$

Свойства на произведението на геометрична прогресия

Произведението на първите ${\displaystyle n}$ члена на геометричната прогресия ${\displaystyle \left\{a_{n}\right\}}$ се нарича произведението от ${\displaystyle a_{1}}$ до ${\displaystyle a_{n}}$ и е израз от вида ${\displaystyle P_{n}=\prod \limits _{i=1}^{n}a_{i}=a_{1}\cdot a_{2}\cdot a_{3}\cdot \ldots \cdot a_{n-2}\cdot a_{n-1}\cdot a_{n}.}$

• ${\displaystyle P_{n}={a}_{1}^{n}\cdot {q}^{\frac {n\left(n-1\right)}{2}}}$
• ${\displaystyle a_{n+1}={\dfrac {P_{n+1}}{P_{n}}}}$
• ${\displaystyle P_{2n}=P_{n}\cdot {\sqrt[{3}]{P_{3n}}}}$
• ${\displaystyle {\sqrt[{k}]{P_{k}^{l-m}}}\cdot {\sqrt[{l}]{P_{l}^{m-k}}}\cdot {\sqrt[{m}]{P_{m}^{k-l}}}=1.}$

Примери за приложения

Геометричната прогресия описва процеси на нарастване или намаляване, в които измерената стойност на променливата в ${\displaystyle (n+1)}$-ия момент от време се получава от тази в ${\displaystyle n}$-ия момент от време чрез умножение по постоянно число ${\displaystyle q}$.

Сложна лихва

 Основна статия: Лихва

При лихвен процент 5 % вложените пари се увеличават всяка година с коефициент 1,05. По този начин капиталът се развива от година на година като членовете на геометрична прогресия с частно ${\displaystyle q=1{,}05}$. В този случай числото ${\displaystyle q}$ означава нарастването на главницата при съответния лихвен процент. С начален капитал от 1000 евро тогава се получава:

• след една година

${\displaystyle 1000\,}$ евро ${\displaystyle \cdot 1{,}05=1050\,}$ евро

• след две години

${\displaystyle 1000\,}$ евро ${\displaystyle \cdot 1{,}05^{2}=1102{,}50\,}$евро

• след три години

${\displaystyle 1000\,}$ евро ${\displaystyle \cdot 1{,}05^{3}=1157{,}63\,}$евро

и така нататък.

Нееластичен удар

Една топка пада на земята от начална височина ${\displaystyle h_{0}}$. След всяко съприкосновение със земята тя отскача обратно нагоре, но губи фиксиран процент ${\displaystyle p\%}$ от височината на скока си поради триене. След ${\displaystyle n}$ удара височините на скока на топката ${\displaystyle h_{n}}$ образуват геометрична прогресия с първоначален член ${\displaystyle h_{0}}$ и частно ${\displaystyle q=1-p\%}$.

Настройка на равно ниво

 Основна статия: Темпериран строй

Геометрична прогресия се среща и в музикологията. Започвайки от определена начална честота, последователността от октави съответства на геометрична прогресия със съотношение 2 (насочваща се към дискантите), последователността от чисти квинти (тези от Питагоровия акорд) – на геометрична прогресия със съотношение 3/2, последователността от полутонове на темперирания строй – на геометрична прогресия със съотношение корен 12-и от 2. Темперираният строй използва само 12 чисти квинти, (3/2)¹² ≈ 129,746, които са на стойност „почти“ 7 октави, 2⁷ = 128, т.е. две геометрични прогресии с еднаква начална стойност, едната със съотношение 3/2, другата със съотношение 2, които не могат да съвпадат точно в която и да е точка, съвпадат приблизително за тези стойности.

Има няколко начина, по които може да се настрои музикален инструмент. Един от тях е настройка на едно и също ниво. В него честотното съотношение между два съседни тона винаги е постоянно. При дванадесет звука в октавата, настройката на ${\displaystyle n}$-ия тон тук е:

${\displaystyle f(n)=a_{0}\cdot \left({\sqrt[{12}]{2}}\right)^{n}}$,

където ${\displaystyle a_{0}}$ е „оригиналният тон“ от честотата на камертона, а за ${\displaystyle i}$-тото полутонно стъпаловидно разстояние до тона на камертона ${\displaystyle f(i)}$ е честотата на желания звук.

Така че коефициентът на растеж е ${\displaystyle q={\sqrt[{12}]{2}}}$.

Ред на Ренар

 Основна статия: Ред на Ренар

Редовете на Ренар са система от предпочитани числа, разделящи интервал от 1 до 10 на 5, 10, 20 или 40 стъпки. Множителят между две последователни числа в ред на Ренар е приблизително постоянен (преди закръгляване), а именно 5-ти, 10-ти, 20-ти или 40-ти корен от 10 (съответно приблизително 1,58, 1,26, 1,12 и 1,06), което води до геометрична прогресия (R5, R10, R20. R40).^[5] Този набор от предпочитани числа е предложен около 1877 г. от френския армейски инженер полковник Шарл Ренар и е публикуван в инструкция от 1886 г. за пленени балонни войски. Неговата система е приета от ISO през 1949 г., за да се формира препоръката R3 на ISO, публикувана за първи път през 1953 г. или 1954 г., която се е превърнала в международния стандарт ISO 3.^[5] Едно приложение на числовата редица на Ренард е номиналният ток на електрически предпазители (напр. R10: 1 A, 2 A, 4 A, 5 A, 10 A, 16 A, 20 A, 25 A, 30 A, 40 A, 50 A, 63 A, 100 A, 200 A). Друго често срещано приложение е номиналното напрежение на кондензаторите (напр. R5: 100 V, 160 V, 250 V, 400 V, 630 V).

Е-серии

 Основна статия: Стандартни номинални Е-серии

Стандартни номинални Е-серии се наричат поредици от числа, установени от стандартите, които определят номиналните стойности (номинали) на основните параметри на произвежданите пасивни електронни елементи (резистори, кондензатори, индуктивни бобини).

Номиналните стойности в една серия с номер N образуват геометрична прогресия с първи член 1 и частно 10^1/N. Така всяка от тях може да се получи от предходната чрез умножаване с частното или от следващата чрез разделяне на 10^1/N. Получените стойности от изчисленията от 1 до 10 се закръглят с точност, определена от номера на серията.

Всеки номинал от N-тата серия може да се определи по формулата за n-тия член на геометричната прогресия:

${\displaystyle a_{n}=10^{n/N}=\exp \left({\frac {n}{N}}\cdot \ln 10\right),}$

където номерът на серията ${\displaystyle N=2^{i}.3}$ ,
при ${\displaystyle i=0,\ 1,\ 2,\ ...,\ 6\ }$ се получава ${\displaystyle \ N=3,\ 6,\ 12,\ 24,\ 48,\ 96,\ 192}$;

${\displaystyle n=0,\ 1,\ 2,\ ...,\ N}$ означава поредния номер на номинала в серията.^[6]

Геометрична прогресия от два цикъла стандартни съпротивления на резистори от 1 до 82 Ω от серия E12 с експоненциално изменение.

Вижте също

• Ред (математика)
• Аритметична прогресия
• Аритметично-геометрична прогресия
• Хармонична прогресия
• Числа на Фибоначи
• Показателна функция
• Коефициент на растеж (математика)^{[Бел. 3]}
• Стандартни номинални Е-серии
• Ефект на снежната топка