Обратни тригонометрични функции
From Wikipedia, the free encyclopedia
Remove ads
Обрàтните тригонометрѝчни фу̀нкции, наричани още àркусфункции или циклометрѝчни функции, се дефинират като обратни на тригонометричните функции. Те определят ъгъла, съответстващ на дадена отсечка в единичната окръжност. Това са функциите:

- Аркуссинус , обратна на синус ;
- Аркускосинус , обратна на косинус ;
- Аркустангeнс , обратна на тангeнс ;
- Аркускотангeнс , обратна на котангeнс ;
- Аркуссеканс , обратна на секанс ;
- Аркускосеканс , обратна на косеканс .
Тази статия се нуждае от вниманието на редактор с по-задълбочени познания по Математика. Ако смятате, че имате необходимите знания, подобрете тази страница. |
Обратните тригонометрични функции служат за намиране на ъгъл от която и да е от неговите тригонометрични функции, но също и за обяснение на антипроизводните (първообразите, примитивите) на определени функции. Те се използват широко в инженерството, навигацията, физиката и геометрията.
Аркусфункциите са многозначни, защото съответните им тригонометрични функции са периодични. Стойността на аркусфункцията е множество от ъгли (дъги), за които съответната права тригонометрична функция е равна на даденото число. Например означава множеството от ъгли , синусът от които е . От множеството от стойности на всяка аркусфункция се отделят нейните главни стойности (вижте графиките на главните стойности на аркусфункциите по-долу), които обикновено се имат предвид, когато се говори за тази аркусфункция. В примера главната стойност на е .
Remove ads
Означения и имена
Обратните тригонометрични функции се означават със стандартен или съкратен запис на името им или чрез правата им функция:
В езиците за компютърно програмиране обратните тригонометрични функции обикновено се означават със съкратените форми Asin, Acos и Atan (във Visual Basic); [1] asin, acos и atan (в C++);[2] или ArcSin, ArcCos и ArcTan (в Паскал).[3]
Името на обратната тригонометрична функция се формира от името на съответната права тригонометрична функция чрез добавяне на префикса „aркус-“ (от латински arcus – дъга). Това се дължи на факта, че геометрично стойността на обратната тригонометрична функция може да бъде свързана с дължината на дъгата на единичната окръжност (или ъгъла, обхващащ тази дъга), съответстваща на определен сегмент. По този начин обикновеният синус позволява да се намери хорда, която го свързва по дъга от окръжност, а обратната функция решава обратния проблем. Начинът за обозначаване на обратните тригонометрични функции по този начин се появява при австрийския математик от 18 век Карл Шерфер и е установен благодарение на Лагранж. Специалният символ за обратната тригонометрична функция е използван за първи път от Даниел Бернули през 1729 г. До края на 19 век английската и немската математически школи предлагат други обозначения: , но те не се утвърждават.[4] Само понякога в чуждестранната литература, както и в научни/инженерни калкулатори, се използват обозначения като sin−1, cos−1 за аркуссинус, аркускосинус и т.н. [5] – такова обозначение се счита за не много удобно, тъй като е възможно объркване с функцията, повдигната на степен −1. Объркването се смекчава донякъде от факта, че всяка от реципрочните тригонометрични функции има собствено име, например (cos(x))−1 = sec(x). Предпочита се обаче такова обозначение да не се използва поради неговата двусмисленост. Друг вариант, използван от някои автори, е означение с първа главна буква, заедно с горен индекс −1: Sin−1(x), Cos−1(x ), Tan−1(x) и т.н. Това потенциално избягва объркване със съответната обратна функция, която трябва да бъде представена чрез sin−1(x), cos−1(x) ... или по-добре чрез sin−1 x, cos−1 x и т.н. Обаче се създава още един основен източник на неяснота, особено след като много популярни езици за програмиране на високо ниво (напр. Mathematica и Magma) използват същите тези представяния с главни букви за стандартните тригонометрични функции, докато други (Python, SymPy, NumPy, MATLAB, Maple и др.) използват малки букви.
От 2009 г. насам стандартът ISO 80000-2 уточнява само префикса „arc“ за обратните функции.
Remove ads
Основни съотношения
Удовлетворени са зависимостите:
Remove ads
Функция arcsin
Аркусинус на числото x е стойността на ъгъла y, изразена в радиани, за която

Функцията е непрекъсната и ограничена в цялата си дефиниционна област. Тя е строго нарастваща.
- при
- за
- Дефиниционна област ,
- Област на стойностите .
Свойства на функцията arcsin
- (функцията е нечетна).
- за .
- за
- за
Получаване на функцията arcsin
Дадена е функцията . В цялата си област на определяне тя е частично монотонна, следователно обратното съответствие не е изпълнено по цялата числова линия. Затова се разглежда интервала , в който функцията строго монотонно нараства и приема всички свои стойности само веднъж. Тогава в интервала съществува обратната функция , чиято графика е симетрична на графиката на функцията относно правата .
Remove ads
Функция arccos
Аркускосинус на числото x се нарича такава стойност на ъгъла y, изразена в радиани, за която

Функцията е непрекъсната и ограничена в цялата си дефиниционна област. Тя е строго намаляваща и неотрицателна.
- при
- при
- Дефиниционна област ,
- Област на стойностите .
Свойства на функцията arccos
- Функцията е централно симетрична по отношение на точката тя е индиферентна (нито четна, нито нечетна).
- при
- при
Получаване на функцията arccos
Дадена е функцията . В цялата си дефиниционна област тя е частично монотонна, следователно обратното съответствие не е изпълнено по цялата числова линия. Затова се разглежда интервала , в който функцията строго монотонно намалява и приема всички свои стойности само веднъж. Тогава в интервала съществува обратната функция , чиято графика е симетрична на графиката на функцията относно правата .
Remove ads
Функция arctg
Аркустангенс на числото x се нарича такава стойност на ъгъла изразена в радиани, за която

Функцията е определена по цялата числова линия, навсякъде непрекъсната и ограничена. Тя е строго нарастваща.
- при
- Дефиниционна област .
- Област на стойностите .
Свойства на функцията arctg
- (функцията е нечетна).
- .
- .
- .
- , където е обратен хиперболичен тангенс, ареатангенс.
Получаване на функцията arctg
Дадена е функцията . В цялата си дефиниционна област тя е частично монотонна, следователно обратното съответствие на функцията не е изпълнено. Затова се разглежда интервала , в който функцията строго монотонно нараства и приема всички стойности от своята област на стойностите само веднъж. Тогава в интервала съществува обратната функция , чиято графика е симетрична на графиката на функцията относно правата .
Remove ads
Функция arcctg

Аркустангенс на числото x е стойността на ъгъла y (в радиани), за който
Функцията е дефинирана на цялата числова ос, непрекъсната е и ограничена навсякъде. Тя е строго намаляваща и положителна навсякъде.
- за
- за
- Дефиниционна област
- Област на стойностите
Свойства на функцията arcctg
- Графиката на функцията е централно симетрична спрямо точката Функцията е безразлична (нито четна, нито нечетна).
- за всеки
Получаване на функция arcctg
Дадена е функцията . В цялата си дефиниционна област тя е частично монотонна и следователно обратното съответствие не съществува. Затова се разглежда интервала , в който функцията строго монотонно намалява и приема всички стойности от своята област само веднъж. Тогава в интервала съществува обратна функция , чиято графика е симетрична на графиката на функцията спрямо правата .
Графиката на функцятаАркускоотангенсна се получава от аркустангенсната графика, ако последната е отразена спрямо ординатната ос (т.е. сменяйки знака на аргумента, ) и е изместена нагоре с π/2; това следва от горната формула
Remove ads
Функция arcsec
Аркуссеканс на числото е стойността на ъгъла (в радиани), за която

.
Функцията е непрекъсната и ограничена в цялата си дефиниционна област. Тя е строго нарастваща и неотрицателна навсякъде.
- при
- при
- Дефиниционна област
- Област на стойностите
- .
Свойства на функцията arcsec
- Графиката на функцията е централно симетрична спрямо точката Функцията е индиферентна (нито четна, нито нечетна).
- за всички
Remove ads
Функция arccosec
Аркосеканс на числото x е стойността на ъгъла y (в радиани), за която

,
Функцията е непрекъсната и ограничена в цялата си област на определение. Тя е строго намаляваща.
- при
- при
- Дефиниционна област ,
- Област на стойностите .
Свойства на функцията arccosec
- (функцията е нечетна).
Remove ads
Сравнение и обобщение
 (червено) и (синьо) |
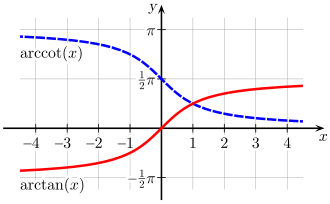 (червено) и (синьо) |
 (червено) и (синьо) |
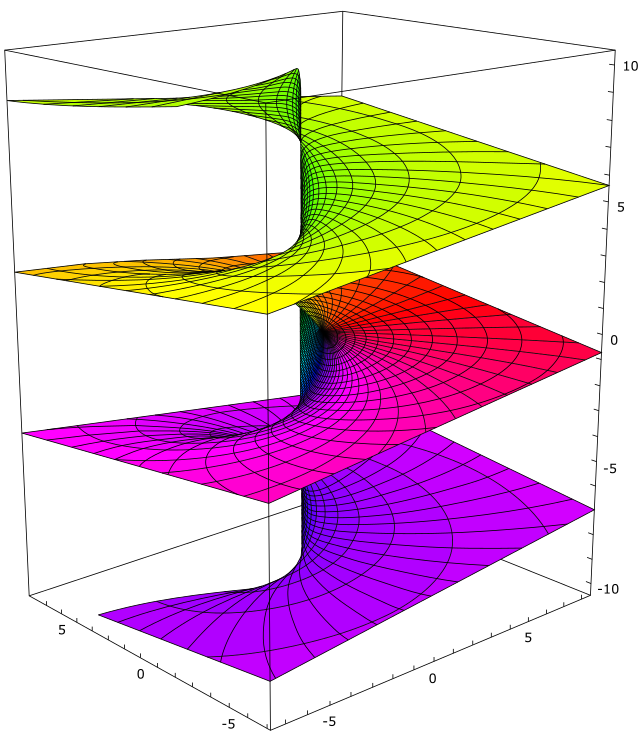
Тъй като тригонометричните функции са периодични функции, те първоначално не са обратими. Ако обаче се ограничи до интервал на монотонност на съответната изходна функция, например интервала или , тогава ограничената функция, получена по този начин, може много добре да бъде обърната. Въпреки това, интервалите на монотонност покриват само половин период, както се вижда от графиките на функциите. Въпреки това, ако се знае както синуса, така и косинуса на ъгъл, можете да се определи ъгъла до цели периоди , (вижте фигурата на вдясно за илюстрация и atan2 за изчисление).
Remove ads
Връзки между функциите
Вижте също: Тригонометрична функция: връзки между функциите
Aркусфункциите могат да бъдат преобразувани една в друга, както следва ( обозначава знаковата функция):
Remove ads
Разложение в редове
- за всички [6]
- за всички
- за всички
Remove ads
Източници и бележки
Вижте още
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads
























































































![{\displaystyle \qquad D(\arcsin x)=[-1;1]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/24a12fa9b5d90522f4e46afa88d54319a3b01c52)
![{\displaystyle \qquad E(\arcsin x)=\left[-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/fc211ba167a472b440dfd7f4101730cf900bf666)












![{\displaystyle [-\pi /2;\pi /2]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/e194f6091eb1b362d19112a5bffdab91ef2a07df)






![{\displaystyle \qquad D(\arccos x)=[-1;1]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/1047e47a84b46e0442cbaa8671f008c10d01d320)
![{\displaystyle \qquad E(\arccos x)=[0;\pi ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/325e024ba344068f583c9d1bd1169547338e07bc)














![{\displaystyle [0;\pi ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/45ba33419dc889bf6c0c684b11285afda3437c95)














































![{\displaystyle D(\operatorname {arcsec} x)=(-\infty ;-1]\cup [1,\infty )}](http://wikimedia.org/api/rest_v1/media/math/render/svg/b695ee3cfd14549d3658ed09adb3e866f10d8dee)
![{\displaystyle E(\operatorname {arcsec} x)=[0;{\frac {\pi }{2}})\cup ({\frac {\pi }{2}};\pi ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/1eb694ab2102821262ea7a660bd0731078054e0f)












![{\displaystyle D(\operatorname {arccosec} x)=(-\infty ;-1]\cup [1,\infty )}](http://wikimedia.org/api/rest_v1/media/math/render/svg/958af4d0d9d94545077f4ce2f680663e382e9bdf)
![{\displaystyle \quad E(\operatorname {arccosec} x)=[-{\frac {\pi }{2}};0)\cup (0;{\frac {\pi }{2}}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/ca1d329fd918df2d0ec3051341b16fe46777faa0)











![{\displaystyle [-\pi /2,\pi /2]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/cd702a5a7041be010f870c0e23750d98ba9919f5)
![{\displaystyle [0,\pi ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751)


 ...
...































