Платоново тяло

Платоновите тела (наричани още правилни многостени) са тези изпъкнали многостени, които имат еднакви многостенни ъгли и чиито стени са еднакви правилни многоъгълници.

Съществуват само пет такива многостена.

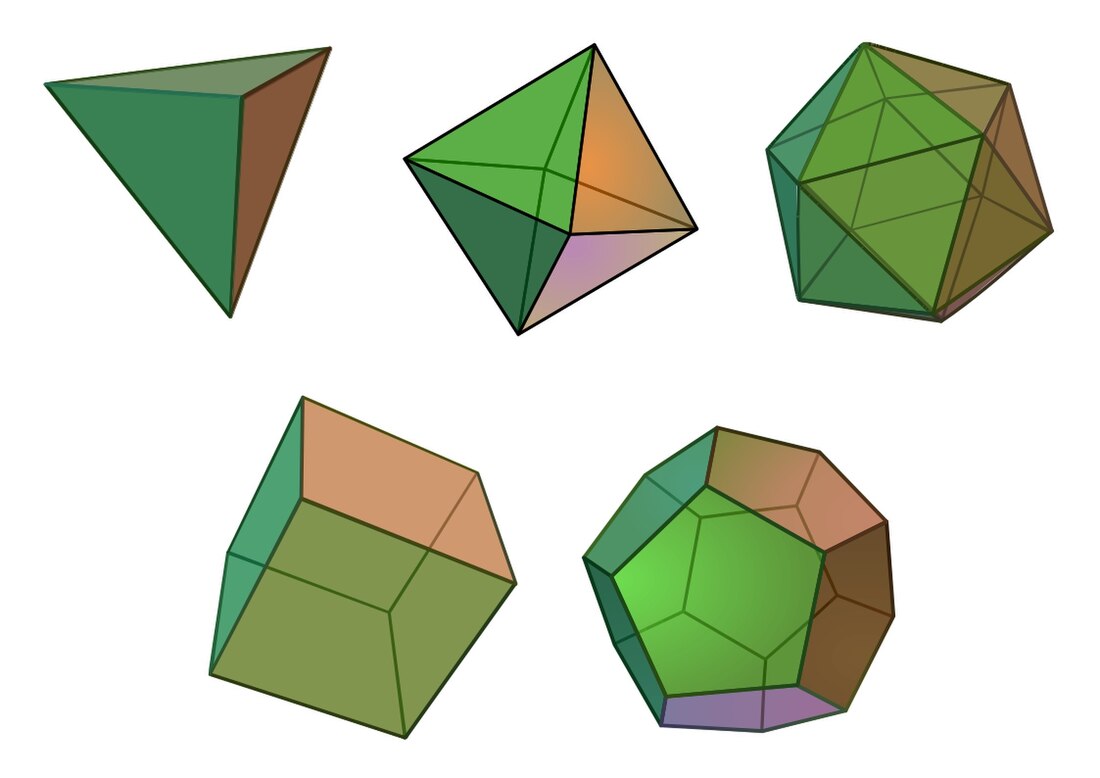
Обяснението е в това, че за многостенен (телесен) ъгъл с n ръба, сборът от ръбните ъгли трябва да бъде по-малък от 360 градуса, като ъглите на правилните многоъгълници могат да бъдат само 108, 90 и 60 градуса, съответстващи на петоъгълник, четириъгълник и триъгълник. Така в един връх на платоново тяло могат да се срещат три петоъгълника, три четириъгълника, и три, четири или пет триъгълника. Поради тази причина съществуват само пет платонови тела (правилни многостени). Така подредени, те се наричат: додекаедър (дванадесетостен); хексаедър (шестостен), по-често наричан куб; тетраедър (четиристен); октаедър (осмостен) и икосаедър (двадесетостен).

Платоново тяло	Стени	Брой стени	Брой ръбове	Брой върхове	Брой стени през връх	Повърхнина S	Обем V	Картинка
Тетраедър	триъгълник	4	6	4	3	${\displaystyle S=a^{2}{\sqrt {3}}}$	${\displaystyle V={\frac {a^{3}{\sqrt {2}}}{12}}}$
Хексаедър (куб)	квадрат	6	12	8	3	${\displaystyle S=6a^{2}\,}$	${\displaystyle V=a^{3}\,}$
Октаедър	триъгълник	8	12	6	4	${\displaystyle S=2a^{2}{\sqrt {3}}}$	${\displaystyle V={\frac {a^{3}{\sqrt {2}}}{3}}}$
Додекаедър	петоъгълник	12	30	20	3	${\displaystyle S=3a^{2}{\sqrt {5(5+2{\sqrt {5}})}}}$	${\displaystyle V={\frac {a^{3}(15+7{\sqrt {5}})}{4}}}$
Икосаедър	триъгълник	20	30	12	5	${\displaystyle S=5a^{2}{\sqrt {3}}}$	${\displaystyle V={\frac {5a^{3}(3+{\sqrt {5}})}{12}}}$

Свойства

Платоновите тела има множество интересни (нетривиални) свойства.

Дуалност на куб и октаедър

Тъй като са изградени от правилно разположени правилни многоъгълници, то центровете на стените им също образуват платонови тела. Така центровете на стените на куба образуват октаедър и, обратно, центровете на октаедър образуват куб. Аналогично свойство имат додекаедърът и икосаедърът. При тетраедъра се получава пак тетраедър. Това свойство се описва като 'дуалност' и то е израз на симетрията, присъща на трите различаващи се случая.

За платоновите тела е в сила една обща формула, свързваща броя на елеметите (стени, върхове, ръбове), от които са изградени; записана неформално тя има вида:

стени + върхове = ръбове + 2 .

Числото две е т.нар. 'ойлерова характеристика' на общия клас, в който попадат и платоновите тела. Отношенията на дуалност са свързани също с тази формулата.