P-адично число

Теорията на P-адичните числа е разработена от немския математик Курт Хензел през 1897 г. (p-adischen Zahlen). Неговият ученик, руският математик Александър М. Островски, доказва теорема (наречена по-късно на негово име), че множеството на рационалните числа може да се допълни до непрекъснато множество само по два начина – или като се използват ирационални числа, или P-адични числа.

3-адични цели числа и връзката им със съответните дуални групи на Понтрягин

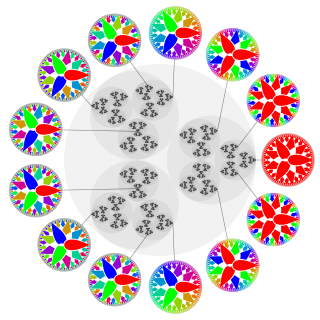
Най-просто казано P-адично число се нарича рационално число, записано с основа просто число, т.е. като редица от остатъци по модул p, където p е просто число.

За основа може да се вземе кое да е просто число (освен 1) (както можем да запишем едно и също цяло число в осмична, 10на, 16на система съответно с основа 8,10,16, така можем да запишем едно реално число в P-адична система с основа 2,3,5 7 и т.н.).

Формалната дефиниция на понятието от теория на числата е: P-адично число^[1] дефинира за фиксирано p което е просто число разширение на множеството на рационалните числа. Това разширение е попълване на полето на рационалните числа на база на P-адичната норма, определена на база делимостта на целите числа на p.

Цяло P-адично число за дадено Просто число p се нарича безкрайният ред ${\displaystyle x=\{x_{1},x_{2},\ldots \}}$${\displaystyle x_{n}}$ по модул ${\displaystyle p^{n}}$, където:

${\displaystyle x_{n}\equiv x_{n+1}{\pmod {p^{n}}}.}$

За разлика от реалните числа, множеството на P-адичните не е подредено, а геометрията на тяхна основа е не-Архимедова.

Тези числа се оказват извънредно полезни при решаването на някои сложни математически задачи, примерно в теория на числата при оценка решимостта на алгебричните уравнения.

По-късно P-адичните числа намират приложение и в квантовата физика, а разработените на тяхна база ултраметрични пространства на Марк Краснер и аделната формула на Фройнд-Витен – в квантовата механика.

Вижте също

• Делимост
• Прости числа
• Естествени числа
• Цели числа
• Рационални числа
• Ирационални числа
• Комплексни числа