শীর্ষ প্রশ্ন
সময়রেখা
চ্যাট
প্রসঙ্গ
সংখ্যা
উইকিপিডিয়া থেকে, বিনামূল্যে একটি বিশ্বকোষ
Remove ads
সংখ্যা হলো পরিমাপের একটি বিমূর্ত ধারণা । সংখ্যা প্রকাশের প্রতীকগুলিকে বলা হয় অঙ্ক । এর প্রকৃত উদাহরণগুলি হল স্বাভাবিক সংখ্যা ১, ২, ৩, ৪ এবং আরও অনেক কিছু।
ইতিহাস
সংখ্যা
সংখ্যাগুলিকে সংখ্যা থেকে আলাদা করা উচিত, চিহ্নগুলি সংখ্যার প্রতিনিধিত্ব করতে ব্যবহৃত হয়৷ মিশরীয়রা প্রথম সাইফার্ড সংখ্যা পদ্ধতি উদ্ভাবন করেছিল এবং গ্রীকরা তাদের গণনা সংখ্যাকে আয়োনিয়ান এবং ডরিক বর্ণমালায় ম্যাপ করে অনুসরণ করেছিল। [১] রোমান সংখ্যা, একটি সিস্টেম যা রোমান বর্ণমালার অক্ষরগুলির সংমিশ্রণ ব্যবহার করে, 14 শতকের শেষের দিকে উচ্চতর হিন্দু-আরবি সংখ্যা পদ্ধতির প্রসার না হওয়া পর্যন্ত ইউরোপে প্রভাবশালী ছিল এবং হিন্দু-আরবি সংখ্যা পদ্ধতি প্রতিনিধিত্ব করার জন্য সবচেয়ে সাধারণ পদ্ধতি হিসাবে রয়ে গেছে। আজ বিশ্বের সংখ্যা। [২] সিস্টেমের কার্যকারিতার চাবিকাঠি ছিল শূন্যের প্রতীক, যা 500 খ্রিস্টাব্দের দিকে প্রাচীন ভারতীয় গণিতবিদরা তৈরি করেছিলেন। [২]
Remove ads
সংখ্যা পদ্ধতি
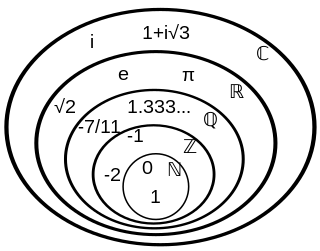
সংখ্যার শ্রেণিবিভাগ
সংখ্যাঃ বাস্তব সংখ্যা ও অবাস্তব সংখ্যা; বাস্তব সংখ্যাঃ মূলদ সংখ্যা ও অমূলদ সংখ্যা; মূলদ সংখ্যাঃ পূর্ণ সংখ্যা ও ভগ্নাংশ সংখ্যা;পূর্ণ সংখ্যাঃ ধনাত্মক পূর্ণ সংখ্যা বা স্বাভাবিক সংখ্যা, শূন্য ও ঋণাত্মক পূর্ণ সংখ্যা ;
স্বাভাবিক সংখ্যা
পূর্ণ সংখ্যা
মূলদ সংখ্যা ও অমূলদ সংখ্যা
বাস্তব সংখ্যা
জটিল সংখ্যা
√-1=i জটিল সংখ্যার প্রতীক
সংখ্যা ধারণার উৎপত্তি
সারাংশ
প্রসঙ্গ
প্রস্তর যুগ
বর্তমান গণিতের জন্ম হয়েছে গণনা থেকে। গণনার ধারণা থেকেই প্রথম সংখ্যা ব্যবহারের প্রয়োজনীয়তা অনুভূত হয়েছিল যদিও সংখ্যার জন্ম হয়েছে অনেক সময়ের ব্যবধানে। প্রাচীন প্রস্তর যুগে মানুষ যখন গুহায় বসবাস করতো তখনও এক-দুই পর্যন্ত গণনা চালু ছিল বলে ধারণা করা হয়। তখন পারিবারিক বা সামাজিক জীবন ভালো করে শুরু না হলেও পদার্থের রূপ সম্বন্ধে তারা ওয়াকিবহাল ছিল। নব্য প্রস্তর যুগে মানুষ খাদ্য আহরণ, উৎপাদন এবং সঞ্চয় করতে শুরু করে। মৃৎ, কাষ্ঠ এবং বয়ন শিল্পের প্রসার ঘটে যার অনেক নমুনা বর্তমানে আবিষ্কৃত হয়েছে। অধিকাংশের মতে এ সময়েই ভাষার বিকাশ ঘটে। তবে ভাষা যতটা বিকশিত হয়েছিল তার তুলনায় সংখ্যার ধারণা ছিল বেশ অস্পষ্ট। সংখ্যাগুলো সর্বদাই বিভিন্ন বস্তুর সাথে সংশ্লিষ্ট থাকতো। যেমন, পশুটি, দুটি হাত, একজোড়া ফল, এক হাঁড়ি মাছ, অনেক গাছ, সাতটি তারা ইত্যাদি। এমনকি অস্ট্রেলিয়া, আমেরিকা এবং আফ্রিকার অনেক গোত্র আজ থেকে মাত্র দুশো বছর আগেও এ অবস্থায় ছিল।
বিশুদ্ধ সংখ্যার ধারণা
বিশুদ্ধ সংখ্যা বলতে বস্তু নিরপেক্ষ সংখ্যার ধারণাকে বুঝায়। প্রস্তর যুগ পেরিয়ে আরও অনেক পরে এ ধারণার বিকাশ ঘটেছে। এক বা দুইয়ের গণ্ডী পেরিয়ে আরও বড় সংখ্যা নির্দেশ করতে প্রথম কেবল যোগ ব্যবহার করা হতো। পরে ধীরে ধীরে যোগ এবং গুণনের সাহায্যে ছোট থেকে বড় সংখ্যার দিকে যাওয়া শুরু হয়। দুটি অস্ট্রেলীয় গোত্রের উদাহরণ এখানে উল্লেখ্য:
- মারে রিভার গোত্র: এনিয়া (এক), পেচেভাল (দুই), পেচেভাল-এনিয়া (তিন), পেচেভাল-পেচেভাল (চার)।
- কামিলা রোই গোত্র: মাল (এক), বুলান (দুই), গুলিবা (তিন), বুলান-বুলান (চার), বুলান-গুলিবা (পাঁচ), গুলিবা-গুলিবা (ছয়)।
সংখ্যার ধারণা স্পষ্ট হতে শুরু করে বাণিজ্যের প্রসারের সাথে সাথে। কারণ এ সময় হিসাব সংরক্ষণ প্রক্রিয়ার প্রয়োজন পড়ে এবং এক গোত্রের সাথে আরেক গোত্রের তথ্যের আদান প্রদান জরুরি হয়ে উঠে। একটি স্পষ্ট সংখ্যা ধারণার উদাহরণ হিসেবে বাংলা সংখ্যা পদ্ধতির কথা বলা যেতে পারে। দশমিক প্রণালী ব্যবহার করে এখানে সংখ্যা গণনা করা হয়ে থাকে। এক থেকে দশ পর্যন্ত হল মূল সংখ্যা।
সংখ্যাকে বিভিন্ন ব্যবস্থায় প্রকাশ করা সম্ভব:
Remove ads
দশমিক ব্যবস্থা
এই ব্যবস্থায় সংখ্যার একেকটি অঙ্ক দশের এককটি গুণিতক।
অনেক একককে দশের বিভিন্ন গুণিতকে প্রকাশ করার জন্য বিশেষ উপসর্গ আছে:
- কিলো (kilo)
- মেগা (Mega)
- গিগা (Giga)
- টেরা (Tera)
- পেটা (Peta)
- এক্সা (Exa)
- জেত্তা (Zetta)
- ইয়ত্তা (Yotta)
- ডেসি (Deci)
- সেন্টি (Centi)
- মিলি (Milli)
- মাইক্রো (Micro)
- ন্যানো (Nano)
- পিকো (Pico)
- ফেম্টো (Femto)
- অ্যাটো (Eto)
- জেপ্টো (Zepto)
বাইনারি ব্যবস্থা
বাইনারি সংখ্যা ব্যবস্থায় শুধু দুইটি অঙ্ক, ০ ও ১ ব্যবহার করা হয়। যেমন, দশমিক ৬ সংখ্যাটি বাইনারিতে প্রকাশিত হবে ১১০ হিসাবে। প্রতিটি অবস্থানের গুরুত্ব (weight) ২ করে, অর্থাৎ ৬ = ১* ২২+১* ২১+১* ২০। এই সংখ্যা পদ্ধতির সুবিধা হল ইলেক্ট্রনিক বর্তনীতে খুব সহজেই বাইনারি সংখ্যার হিসাব করা যায়, ফলে কম্পিউটার ও ডিজিটাল বর্তনীতে এই সংখ্যা ব্যবস্থার ব্যাপক প্রচলন রয়েছে।
আরও দেখুন
তথ্যসূত্র
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads
