শীর্ষ প্রশ্ন
সময়রেখা
চ্যাট
প্রসঙ্গ
লম্বন
উইকিপিডিয়া থেকে, বিনামূল্যে একটি বিশ্বকোষ
Remove ads
দর্শকের দুইটি ভিন্ন অবস্থানের সাথে কোন খ-বস্তু(celestial body) যে কোণ উৎপন্ন করে থাকে তাকে লম্বন বলে। এই দুই অবস্থানের একটি পৃথিবীর কেন্দ্র এবং অপরটি ভূপৃষ্ঠস্থ কোন স্থান হয়ে থাকলে ভিত্তি রেখাটি(base line) হয় পৃথিবীর ব্যাসার্ধের সমান। এই প্রকারের লম্বনকে বলা হয় আহ্নিক লম্বন। আর দুই অবস্থানের একটি পৃথিবীর কেন্দ্র এবং অপরটি সূর্যের কেন্দ্র হয়ে থাকলে ভিত্তিরেখাটি হবে পৃথিবীর কক্ষপথের গড় ব্যাসার্ধের সমান। এই দ্বিতীয় প্রকারের লম্বনকে বার্ষিক লম্বন বলা হয়।
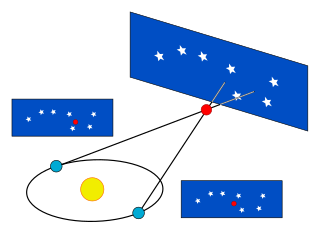
পৃথিবী থেকে গ্রহ বা নক্ষত্রের দূরত্বের মতো বড় দূরত্ব পরিমাপ করতে, জ্যোতির্বিজ্ঞানীরা প্যারালাক্স নীতি ব্যবহার করেন।
এখানে, প্যারালাক্স শব্দটি হল নক্ষত্রের দুটি দৃষ্টি-রেখার মধ্যে প্রবণতার আধা-কোণ, যেমনটি দেখা যায় যখন পৃথিবী তার কক্ষপথে সূর্যের বিপরীত দিকে থাকে।
এই দূরত্বগুলিকে "মহাজাগতিক দূরত্বের মই" বলা হয়, যাকে বলা হয় তার সর্বনিম্ন স্তর তৈরি করে, প্রথমটি পদ্ধতির ধারাবাহিকতায় যার মাধ্যমে জ্যোতির্বিজ্ঞানীরা মহাকাশীয় বস্তুর দূরত্ব নির্ধারণ করে, জ্যোতির্বিদ্যায় অন্যান্য দূরত্ব পরিমাপের ভিত্তি হিসাবে কাজ করে যা উচ্চতর স্তর তৈরি করে।
প্যারালাক্স রাইফেল স্কোপ, বাইনোকুলার, মাইক্রোস্কোপ এবং টুইন-লেন্স রিফ্লেক্স ক্যামেরার মতো অপটিক্যাল যন্ত্রগুলিকেও প্রভাবিত করে যা বস্তুগুলিকে সামান্য ভিন্ন কোণ থেকে দেখে।
মানুষের সাথে অনেক প্রাণীর দুটি চোখ ওভারল্যাপিং ভিজ্যুয়াল ক্ষেত্র রয়েছে যা গভীরতা উপলব্ধি করতে প্যারালাক্স ব্যবহার করে;
এই প্রক্রিয়া স্টেরিওপসিস নামে পরিচিত।
কম্পিউটার ভিশনে প্রভাবটি কম্পিউটার স্টেরিও ভিশনের জন্য ব্যবহৃত হয়, এবং একটি প্যারালাক্স রেঞ্জফাইন্ডার নামে একটি ডিভাইস রয়েছে যা এটি পরিসীমা খুঁজে পেতে ব্যবহার করে, এবং কিছু বৈচিত্র্যের ক্ষেত্রেও একটি লক্ষ্যের উচ্চতা।
প্যারালাক্সের একটি সাধারণ দৈনন্দিন উদাহরণ মোটর গাড়ির ড্যাশবোর্ডগুলিতে দেখা যায় যা একটি সুই-স্টাইলের যান্ত্রিক স্পিডোমিটার ব্যবহার করে।
সরাসরি সামনে থেকে দেখা হলে, গতি ঠিক 60 দেখাতে পারে, কিন্তু যাত্রীর আসন থেকে দেখা হলে, সূচটি বিমানের সমতল থেকে সুচের স্থানচ্যুতির সাথে মিলিত দেখার কোণের কারণে কিছুটা ভিন্ন গতি দেখাতে পারে।
সংখ্যাসূচক ডায়াল।
Remove ads
দূরত্ব পরিমাপ
সারাংশ
প্রসঙ্গ
পর্যবেক্ষক, পর্যবেক্ষিত বা উভয়ের গতির কারণে দৃষ্টিভঙ্গির পরিবর্তনের কারণে প্যারালাক্সের উদ্ভব হয়।
যা অপরিহার্য তা হল আপেক্ষিক গতি।
প্যারালাক্স পর্যবেক্ষণ করে, কোণ পরিমাপ করে এবং জ্যামিতি ব্যবহার করে দূরত্ব নির্ণয় করা যায়।
প্যারালাক্স দ্বারা দূরত্ব পরিমাপ হল ত্রিভুজ নীতির একটি বিশেষ কেস, যা বলে যে কেউ ত্রিভুজের নেটওয়ার্কের সমস্ত বাহু এবং কোণের সমাধান করতে পারে যদি নেটওয়ার্কের সমস্ত কোণ ছাড়াও, কমপক্ষে এক বাহুর দৈর্ঘ্য পরিমাপ করা হয়েছে। এইভাবে, একটি বেসলাইনের দৈর্ঘ্যের যত্নশীল পরিমাপ একটি সম্পূর্ণ ত্রিভুজ নেটওয়ার্কের স্কেল ঠিক করতে পারে।
প্যারালাক্সে, ত্রিভুজটি অত্যন্ত দীর্ঘ এবং সরু, এবং এর ক্ষুদ্রতম দিক (পর্যবেক্ষকের গতি) এবং ছোট শীর্ষ কোণ (সর্বদা 1" এর কম, বাকি দুটিকে 90° এর কাছাকাছি রেখে) উভয়ই পরিমাপ করে,
দীর্ঘ দিকগুলি (অভ্যাসে সমান বলে বিবেচিত) নির্ধারণ করা যেতে পারে।
জ্যোতির্বিদ্যায়, কোণটি ছোট বলে ধরে নিলে, একটি তারার দূরত্ব (পারসেক এ পরিমাপ করা হয়) প্যারালাক্সের পারস্পরিক (আর্কসেকেন্ডে পরিমাপ করা হয়):
𝑑(pc)=1/𝑝(আর্কসেকেন্ড)।
উদাহরণস্বরূপ, প্রক্সিমা সেন্টোরির দূরত্ব হল 1/0.7687 = 1.3009 পারসেক (4.243 আলোকবর্ষ)।
পৃথিবীতে, একটি কাকতালীয় রেঞ্জফাইন্ডার বা প্যারালাক্স রেঞ্জফাইন্ডার একটি লক্ষ্যের দূরত্ব খুঁজে পেতে ব্যবহার করা যেতে পারে।
সমীক্ষায়, অজানা বিন্দুর স্থানাঙ্ক নির্ণয় করার জন্য একটি পরিচিত বেসলাইন থেকে কৌণিক পরিমাপ অন্বেষণ করা হয়।
··· ··· ··· ··· ··· ··· ··· ··· ··· ··· ··· ··· ··· ··· ··· ···
❝দার্শনিক টুইস্ট যোগ করা হবে (সাম্বলতার সাথে), অবশ্যই, পর্যবেক্ষণ করা দূরত্বটি কেবল "বিষয়ভিত্তিক" নয়, যেহেতু একই বস্তু যেটি "সেখানে" বিদ্যমান তা দুটি ভিন্ন অবস্থান বা দৃষ্টিকোণ থেকে দেখা যায়।
বরং এটা হল যে, হেগেল যেমন বলতেন, বিষয় এবং বস্তু সহজাতভাবে "মধ্যস্থতা" হয় যাতে বিষয়ের দৃষ্টিকোণে একটি "জ্ঞানতাত্ত্বিক" স্থানান্তর সর্বদা বস্তুর মধ্যে একটি "অন্টোলজিক্যাল" পরিবর্তন প্রতিফলিত করে।
অথবা—এটিকে ল্যাকানিজে বলতে গেলে—বিষয়ের দৃষ্টি সর্বদা ইতিমধ্যেই অনুভূত বস্তুর মধ্যেই খোদাই করা হয়, তার "অন্ধ স্থান" এর ছদ্মবেশে, যেটি "বস্তুর থেকেও বেশি বস্তুর মধ্যে," যে বিন্দু থেকে
বস্তু নিজেই দৃষ্টি ফিরিয়ে দেয়।
"অবশ্যই ছবিটি আমার চোখে আছে, কিন্তু আমিও ছবিতে আছি"...❞
—Slavoj Žižek, The Parallax View
| এই নিবন্ধটি অসম্পূর্ণ। আপনি চাইলে এটিকে সম্প্রসারিত করে উইকিপিডিয়াকে সাহায্য করতে পারেন। |
Remove ads
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads
