Vector (física)
From Wikipedia, the free encyclopedia
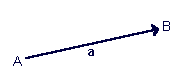
En física un vector és un concepte matemàtic i un segment orientat que s'utilitza per descriure magnituds tals com velocitats, acceleracions o forces, en les quals és important considerar no només el valor sinó també la direcció i el sentit. Es representa per un segment orientat per denotar el seu sentit, la seva magnitud (la longitud de la fletxa) i el punt d'aplicació.
|
|
S'ha proposat fusionar aquest article a «Vector (matemàtiques)». (Vegeu la discussió, pendent de concretar). Data: 2019 |