Procés adiabàtic

Un procés adiabàtic és aquell en el qual el sistema termodinàmic (generalment, un fluid que exerceix un treball) no intercanvia calor amb el seu entorn. Un procés adiabàtic que és, a més, reversible, és un procés isentròpic.

Gràfica d'un procés adiabàtic en funció de la pressió ${\displaystyle P}$ i el volum ${\displaystyle V}$. La corba adiabàtica (en blau) segueix l'equació: ${\displaystyle P=K/V^{\gamma }}$ on ${\displaystyle K=P_{A}V_{A}^{\gamma }=P_{B}V_{B}^{\gamma }}$. L'àrea groga és el treball associat al canvi entre els punts A i B.

Etimològicament, «adiabàtic» és un mot format per la partícula a–, prefix que prové del grec a–, que significa ‘no’, ‘sense’, usat en la formació de mots cultes; i diabàtic que prové del grec διαβατικός diabatikós 'que pot travessar o traspassar'. Per tant, «adiabàtic» significa ‘que no pot travessar’.^[1][2]

En tot procés adiabàtic experimentat per un gas ideal es compleixen les següents relacions:

Cicle d'Otto. Les etapes 1-2 i 3-4 són adiabàtiques.

$${\displaystyle P_{1}V_{1}^{\gamma }=P_{2}V_{2}^{\gamma }}$$$${\displaystyle T_{1}V_{1}^{\gamma -1}=P_{2}V_{2}^{\gamma -1}}$$$${\displaystyle T_{1}^{\gamma }P_{1}^{1-\gamma }=T_{2}^{\gamma }P_{2}^{1-\gamma }}$$on:

• ${\displaystyle 1}$ fa referència a l'estat inicial abans del procés i ${\displaystyle 2}$ a l'estat després de finalitzar el procés.
• ${\displaystyle P}$ és la pressió.
• ${\displaystyle V}$ és el volum.
• ${\displaystyle T}$ és la temperatura absoluta o termodinàmica.
• ${\displaystyle \gamma }$ és el coeficient adiabàtic definit per ${\displaystyle \gamma =C_{P}/C_{V}}$, on ${\displaystyle C_{P}}$ és la capacitat calorífica del gas a pressió constant i ${\displaystyle C_{V}}$ és la capacitat calorífica del gas a volum constant. En principi, el coeficient adiabàtic és funció de la temperatura i de la pressió, però per als gasos ideals a temperatura ambient només depèn de la composició. ${\displaystyle \gamma }$ = 5/3 = 1,67 per a un gas monoatòmic ideal (heli, neó, argó...) i ${\displaystyle \gamma }$ = 7/5 = 1,40 per a gasos diatòmics (H₂, O₂, N₂...).^[3]

Cicle de Diesel. Les etapes 1-2 i 3-4 són adiabàtiques

L'extrem oposat, en el qual té lloc la màxima transferència de calor, causant que la temperatura romangui constant, es denomina procés isotèrmic. El terme adiabàtic fa referència a elements que impedeixen la transferència de calor amb l'entorn. Una paret aïllada s'aproxima bastant a un límit adiabàtic. És el cas d'una paret d'un calorímetre.

Els processos adiabàtics apareixen en algunes etapes de cicles termodinàmics com ara el de Carnot; el cicle d'Otto emprat en els motors de quatre temps dels motors d'explosió que cremen gasolina; o el cicle de Diesel, emprat als motors diesel que empren gasoil.^[3]

N'és un altre exemple la temperatura adiabàtica de flama, que és la temperatura que podria arribar a una flama si no hi hagués pèrdua de calor cap a l'entorn. En climatització, els processos d'humectació (aportació de vapor d'aigua) són adiabàtics, ja que no hi ha transferència de calor, malgrat que s'aconsegueixi variar la temperatura de l'aire i la seva humitat relativa. L'escalfament i refredament adiabàtic són processos que comunament ocorren a causa del canvi en la pressió d'un gas. Això pot ser quantificat usant la llei dels gasos ideals.

Descripció

Un procés sense transferència de calor cap a o des d'un sistema, de manera que Q = 0, es diu adiabàtic,^[4] i aquest sistema es diu que està adiabáticamente aïllat.^[5][6] La suposició simplificadora que es fa amb freqüència és que un procés és adiabàtic. Per exemple, se suposa que la compressió d'un gas dins d'un cilindre d'un motor ocorre tan ràpidament que, en l'escala de temps del procés de compressió, una petita part de l'energia del sistema pot transferir-se en forma de calor als voltants. Encara que els cilindres no estan aïllats i són bastant conductors, aquest procés s'idealitza perquè sigui adiabàtic. El mateix pot dir-se del procés d'expansió d'aquest sistema.

La suposició d'aïllament adiabàtic és útil i, sovint, es combina amb altres idealitzacions similars per a calcular una bona primera aproximació del comportament d'un sistema. Per exemple, segons Laplace, quan el so viatja en un gas, no hi ha temps per a la conducció de calor en el mitjà, per la qual cosa la propagació del so és adiabàtica. Per a tal procés adiabàtic, el mòdul d'elasticitat (Mòdul de Young) es pot expressar com E = γP, on γ és la relació de calors específiques a pressió constant i a volum constant (γ = C_p/C_v) i P és la pressió del gas.

Diverses aplicacions de la suposició adiabàtica

Per a un sistema tancat, es pot escriure la primera llei de la termodinàmica com ΔU = Q − W, on ΔU denota el canvi de l'energia interna del sistema, Q la quantitat d'energia afegida en forma de calor, i W el treball fet pel sistema sobre el seu entorn.

Si el sistema té parets tan rígides que el treball no pot transferir-se cap a dins o cap a fora (W = 0), i les parets no són adiabàtiques i s'agrega energia en forma de calor (Q > 0), i no hi ha canvi de fase, llavors la temperatura del sistema augmentarà. Si el sistema té parets tan rígides que no es pot fer treball de pressió-volum, però les parets són adiabàtiques (Q = 0), i l'energia s'agrega com a treball isocòric (volum constant) en forma de fricció o agitació d'un fluid viscós dins del sistema (W < 0), i no hi ha canvi de fase, llavors la temperatura del sistema augmentarà. Si les parets del sistema són adiabàtiques (Q = 0) però no rígides (W ≠ 0), i, en un procés idealitzat fictici, s'agrega energia al sistema en forma de treball de pressió-volum no viscós i sense fricció (W < 0), i no hi ha canvi de fase, llavors la temperatura del sistema augmentarà. Tal procés es diu procés isentròpic i es diu que és "reversible". Idealment, si s'invertís el procés, l'energia podria recuperar-se per complet com a treball fet pel sistema. Si el sistema conté un gas comprimible i el seu volum es redueix, la incertesa de la posició del gas es redueix i aparentment reduiria l'entropia del sistema, però la temperatura del sistema augmentarà, ja que el procés és isentròpic (ΔS = 0). Si el treball s'agrega de tal manera que la fricció o les forces viscoses estan operant dins del sistema, llavors el procés no és isentròpic, i si no hi ha un canvi de fase, llavors la temperatura del sistema augmentarà, es diu que el procés és "irreversible", i el treball agregat al sistema no és completament recuperable en forma de treball. Si les parets d'un sistema no són adiabàtiques i l'energia es transfereix en forma de calor, l'entropia es transfereix al sistema amb la calor. Aquest procés no és ni adiabàtic ni isentròpic, tenint Q > 0, i ΔS > 0 segons la segona llei de la termodinàmica.

Els processos adiabàtics naturals són irreversibles (es produeix entropia).

La transferència d'energia com a treball en un sistema adiabàticament aïllat es pot imaginar com dos tipus extrems idealitzats. En un d'aquests tipus, no es produeix entropia dins del sistema (sense fricció, dissipació viscosa, etc.), i el treball és sol treball de pressió-volum (indicat per P dV). En la naturalesa, aquest tipus ideal ocorre només aproximadament perquè exigeix un procés infinitament lent i sense fonts de dissipació.

L'altre tipus de treball extrem és el treball isocòric. (dV = 0), per al qual l'energia s'agrega com a treball únicament a través de la fricció o la dissipació viscosa dins del sistema. Un agitador que transfereix energia a un fluid viscós d'un sistema aïllat adiabàticament amb parets rígides, sense canvi de fase, provocarà un augment de temperatura del fluid, però aquest treball no és recuperable. El treball isocòric és irreversible.^[7] La segona llei de la termodinàmica observa que un procés natural, de transferència d'energia com a treball, sempre consta almenys de treball isocòric i, sovint, d'aquests dos tipus extrems de treball. Tot procés natural, adiabàtic o no, és irreversible, amb ΔS > 0, ja que la fricció o la viscositat sempre són presents fins a un cert punt.

Refredament adiabàtic de l'aire

Hi ha tres relacions en el refredament adiabàtic de l'aire:

1. La relació ambient de l'atmosfera, que és la proporció en la qual l'aire es refreda a mesura que n'augmenta l'altitud.
2. La taxa seca adiabàtica, és d'un -1 °C per cada 100 metres de pujada.
3. La taxa humida adiabàtica és d'uns -0,6 °C - 0,3 °C per cada 100 metres de pujada.

La primera relació es fa servir per a descriure la temperatura de l'aire circumdant a través del qual està passant l'aire ascendent. La segona i tercera proporció són les referències per a una massa d'aire que està ascendint en l'atmosfera. La taxa seca adiabàtica s'aplica a l'aire que està per sota del punt de rosada, per exemple si no està saturat de vapor d'aigua, mentre que la taxa humida adiabàtica s'aplica a l'aire que ha arribat al seu punt de rosada. El refredament adiabàtic és una causa comuna de la formació de núvols.

El refredament adiabàtic no ha d'involucrar necessàriament un fluid. Una tècnica usada per a arribar a temperatures molt baixes (milionèsimes de grau sobre el zero absolut) és la desmagnetització adiabàtica, en què el canvi en un camp magnètic en un material magnètic es fa servir per a aconseguir un refredament adiabàtic.

Treball exercit per un fluid en procés adiabàtic

La fórmula que quantifica aquest valor ens diu que el treball és proporcional a l'increment dels productes de pressió i volum i inversament proporcional a (1-γ). La lletra grega gamma representa el coeficient adiabàtic, adimensional. Mentre el treball, la pressió i el volum són dimensionals.^[8]

${\displaystyle W=(p_{2}\cdot V_{2}-p_{1}\cdot V_{1})/(1-\gamma )}$

Processos adiabàtics en mecànica quàntica

Article principal: Teorema adiabàtic

En mecànica quàntica, una transformació adiabàtica és un canvi lent hamiltonià quàntic ${\displaystyle {\hat {H}}\,}$ que descriu el sistema, i que dona com a resultat un canvi dels valors propipí del hamiltonià, però no dels seus estats propipí.

Relacions P, V, T en l'expansió adiabàtica del gas ideal

Joule, en el seu cèlebre experiment sobre expansió lliure, va demostrar que l'energia interna d'un gas perfecte era independent del volum (V), o la pressió (P), només funció de la temperatura.

Aquesta conclusió condueix al fet que, per a un gas ideal:

${\displaystyle {\text{(a)}}\qquad dU=n\ C_{v}\ dT=\delta Q-\delta W}$

Però a l'expansió adiabàtica:

${\displaystyle {\text{(b)}}\qquad \delta Q=0;\qquad \delta W=P\ \delta V}$

Amb la qual cosa s'obté la relació següent:

${\displaystyle {\text{(c)}}\qquad \delta U=n\ C_{v}\ \delta T=-P\ \delta V}$

Al gas ideal es compleix:

${\displaystyle P\ V=n\ R\ T}$

${\displaystyle C_{p}-C_{v}=n\ R}$

${\displaystyle \gamma =C_{p}/C_{v}}$

Els valors ${\displaystyle C_{p}}$ i ${\displaystyle C_{v}}$ són funció del nombre d'àtoms en la molècula.

Buidant ${\displaystyle P}$ i substituint ${\displaystyle P}$ i ${\displaystyle R}$ en l'Eq.(c) queda, la relació diferencial:

${\displaystyle {\text{(d)}}\qquad {\frac {dT}{T}}=-{\frac {\left(\gamma -1\right)\ dV}{V}}}$

I integrant entre els estats inicial i final:

${\displaystyle {\text{(e)}}\qquad {\frac {T_{f}}{T_{i}}}=\left({\frac {V_{i}}{V_{f}}}\right)^{\left(\gamma -1\right)}}$

Tenint en compte que en treballar amb gasos perfectes es compleix ${\displaystyle T=PV/nR}$, l'Eq.(e) pot posar-se:

${\displaystyle \qquad {\frac {P_{f}\ V_{f}}{P_{i}\ V_{i}}}=\left({\frac {V_{i}}{V_{f}}}\right)^{\left(\gamma -1\right)}\qquad \to \qquad {\frac {P_{f}}{P_{i}}}=\left({\frac {V_{i}}{V_{f}}}\right)^{\left(\gamma \right)}}$

Finalment:

${\displaystyle {\text{(f)}}\qquad P_{f}V_{f}^{\gamma }=P_{i}V_{i}^{\gamma }=Constant}$

operant sobre Eq.(e) i Eq.(f):

${\displaystyle {\text{(g)}}\qquad {\frac {T_{f}}{T_{i}}}=\left({\frac {P_{f}}{P_{i}}}\right)^{\left({\frac {\gamma -1}{\gamma }}\right)}}$

Càlcul del treball involucrat

Segons es va deduir anteriorment, l'equació que descriu un procés adiabàtic del gas ideal, en un procés reversible: ${\displaystyle PV^{\gamma }=\operatorname {constant} }$ on P és la pressió del gas, V el seu volum i ${\displaystyle \gamma ={C_{P} \over C_{V}}}$ el coeficient adiabàtic, sent ${\displaystyle C_{P}}$ la calor específica molar a pressió constant i ${\displaystyle C_{V}}$ la calor específica molar a volum constant.

Per a un gas monoatòmic ideal, ${\displaystyle \gamma =5/3}$. Per a un gas diatòmic (com el nitrogen o l'oxigen, els principals components de l'aire) ${\displaystyle \gamma =7/5=1,4}$

Com que no hi ha subministrament extern de calor, qualsevol treball (W) realitzat serà a costa de l'energia U, En la fórmula:

${\displaystyle PV^{\gamma }=\operatorname {K} }$

fem un petit canvi, llavors quedaria així:

${\displaystyle P=K/V^{\gamma }\qquad \qquad \qquad (4)}$

Ara derivant la fórmula del treball i integrant-la alhora tenim:

${\displaystyle \int _{1}^{2}\,dW}$ =${\displaystyle \int _{1}^{2}\,PdV\qquad \qquad \qquad (5)}$

Ara reemplacem la (4) a la (5):

${\displaystyle \int _{1}^{2}\,K/{V^{\gamma }}dV}$

Ara sabem que "K" és una constant, per la qual cosa, aquesta surt de la integral:

${\displaystyle K\int _{1}^{2}\,1/{V^{\gamma }}dV}$

després veiem que ens queda tot en funció del volum aleshores ho integrem:

${\displaystyle (KV^{1-{\gamma }})/(1-{\gamma })}$

com sabem que:

${\displaystyle PV^{\gamma }=\operatorname {K} }$

llavors reemplacem a l'equació:

${\displaystyle PV^{\gamma }(V^{1-{\gamma }})_{1}^{2}/(1-{\gamma })}$

i multipliquem:

${\displaystyle (P_{2}V_{2}^{\gamma }V_{2}^{1-{\gamma }}-P_{1}V_{1}^{\gamma }V_{1}^{1-{\gamma }})/(1-{\gamma })}$

després de resoldre l'equació ens quedarà aquesta manera:

${\displaystyle [P_{2}V_{2}-P_{1}V_{1}]/(1-{\gamma })}$

i per definició ens quedaria:

${\displaystyle \Delta (PV)/(1-{\gamma })}$

que al final ens donarà:

${\displaystyle nR\Delta T/(1-{\gamma })}$

i això serà igual a la feina:

${\displaystyle \ W=(P_{2}V_{2}-P_{1}V_{1})/(1-{\gamma })=nR(T_{2}-T_{1})/(1-{\gamma })}$

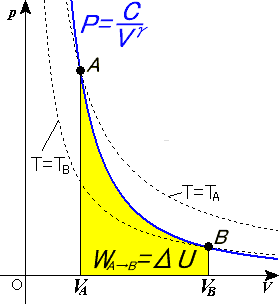
Representació gràfica de les corbes adiabàtiques

Durant un procés adiabàtic, l'energia interna del fluid que fa el treball deu necessàriament decréixer.

Esquema d'una expansió adiabàtica.

Les propietats de les corbes adiabàtiques en un diagrama P-V són les següents:

1. Cada adiabàtica s'aproxima asimptòticament a tots dos eixos del diagrama P-V (igual que les isotermes).
2. Cada adiabàtica s'interseca amb cada isoterma en un sol punt.
3. Una corba adiabàtica s'assembla a una isoterma, excepte que durant una expansió, una adiabàtica perd més pressió que una isoterma, per la qual cosa inclinació és major (és més vertical).
4. Si les isotermes són còncaves cap a la direcció "nord-est" (45°), llavors les adiabàtiques són còncaves cap a la direcció "aquest nord-est" (31°).
5. Si adiabàtiques i isotermes es dibuixen separadament amb canvis regulars en l'entropia i temperatura, llavors a mesura que ens allunyem dels eixos (en direcció nord-est), sembla que la densitat de les isotermes roman constant, però la densitat de les adiabàtiques disminueix. L'excepció es troba molt prop del zero absolut, on la densitat de les adiabàtiques cau fortament i es fan molt rares (Vegeu també: Teorema de Nernst).