Logaritmická spirála
From Wikipedia, the free encyclopedia
Remove ads
Logaritmická spirála je rovinná křivka (spirála), jejíž poloměr roste exponenciálně s velikostí úhlu.
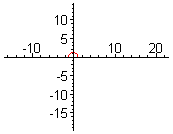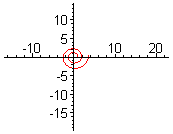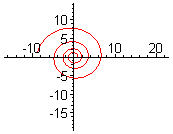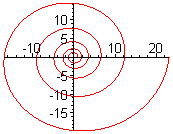
V polární soustavě souřadnic () lze tuto spirálu zapsat rovnicí
- ,
nebo ekvivalentně
- ,
kde
- a je Eulerovo číslo.
Remove ads
Vlastnosti
Důležitými body jsou pól a počátek.
- Pól je bod, kolem kterého se spirála „ovíjí“. Pro neposunutou spirálu se nachází v bodě souřadné soustavy.
- Počátek spirály je bod, od kterého se začíná spirála vykreslovat. Pro neposunutou spirálu se nachází v bodě .
Paprsek vycházející z pólu spirály protíná spirálu v bodech, jejichž vzdálenosti od pólu tvoří geometrickou posloupnost.
Tečný úhel je definován jako úhel, který svírá pro daný bod spirály vektor poloměru s tečnou ve stejném bodě. Spojnice pólu spirály a libovolného jejího bodu protíná logaritmickou spirálu vždy pod stejným tečným úhlem. Proto se logaritmická spirála také nazývá ekviangulární (rovnoúhlá) spirála (René Descartes, 1638).
Další možné vyjadření rovnice logaritmické spirály získáme jednoduchou úpravou:
Z tohoto vztahu také vznikl název „logaritmická spirála“.
Remove ads
Logaritmické spirály v přírodě
Výsledkem některých přírodních jevů jsou útvary, které se podobají logaritmickým spirálám. Zde je výčet několika příkladů:
- Dráha, po níž se draví ptáci (sokoli) přibližují ke své kořisti. Rovnoúhlost spirály jim umožňuje pozorovat kořist pod stálým úhlem.[1][2]
- Dráha, po níž se hmyz přibližuje ke zdroji světla.[3]
- Ramena spirálních galaxií.[4] Galaxie Mléčná dráha má několik spirálních ramen; každé rameno zhruba odpovídá logaritmické spirále se sklonem asi 12 stupňů.[5]
- Pásy oblačnosti tvořící se ve středu tropických cyklón.[6]
- Řada biologických útvarů, například schránky měkkýšů.[7]
Související informace naleznete také v článcích Zlatý řez#Zlatý řez v přírodě a Fibonacciho posloupnost#Význam.
Remove ads
Odkazy
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads
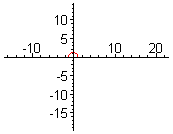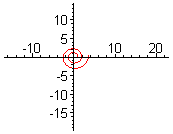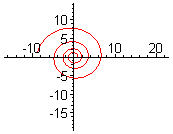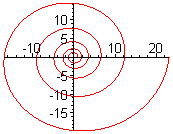





![{\displaystyle [0,0]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/8e543f601fac1a6510c6fd606aee4cae29fc1a79)
![{\displaystyle [a,0]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/5176c1d73f89ef89e52a707410eed22b8ab29a10)
