Maxima (software)

svobodný počítačový algebraický systém From Wikipedia, the free encyclopedia

Maxima (software)
Remove ads

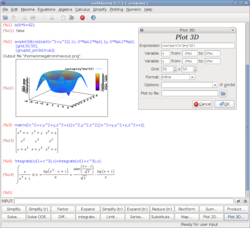
Maxima je svobodný počítačový algebraický systém, napsaný v Lispu (resp. jeho dialektu Common Lisp) a distribuovaný pod GNU General Public License. Je dostupný pro všechny platformy standardu POSIX, jakými jsou Unix, BSD nebo Linux; dostupné jsou také binární soubory pro MS Windows. wxMaxima je multiplatformní verzí s grafickým uživatelským rozhraním, založenou na wxWidgets.

Stručná fakta Aktuální verze, Operační systém ...
Remove ads

Maxima vychází z projektu Macsyma, jenž byl vyvíjen v MIT (Massachusetts Institute of Technology) a financován United States Department of Energy a dalšími vládními organizacemi. O vývoj jedné z verzí Macsyma se staral od roku 1982 až do své smrti v roce 2001 Bill Schelter, jenž v roce 1998 získal svolení uveřejnit svou verzi pod GPL. Tuto verzi, nyní nazývanou Maxima, nyní udržuje nezávislá komunita vývojářů a uživatelů.

Jako interaktivního grafického rozhraní pro Maximu lze využít programu GNU TeXmacs. Dalšími možnostmi jsou front end imaxima nebo interaktivní mód editoru Emacs.

Remove ads

Ovládání Maximy

Při spuštění vypíše Maxima Hlášení o distribuci pod GNU General Public License a pak už rovnou výzvu k zadání příkazu. Od verze 5.9.1 včetně je to (%i1), dříve (C1). Výzvu však můžeme jednoduše změnit nastavením proměnných inchar a outchar.

Základní pravidla pro psaní příkazů:

  • každý příkaz musí končit středníkem – příkaz můžeme rozdělit na více řádků, provede se až po zadání středníku a stisknutí [Enter]
  • Maxima je case sensitive, tzn. rozlišuje velká a malá písmena, z čehož plyne, že solve a SOLVE jsou dva různé příkazy
  • pro násobení se musí používat znak hvězdička * – 2*a je správně, 2a špatně
  • pro umocňování můžeme používat buď symbol stříška ^, nebo dvě hvězdičky **.

Základní aritmetické operace

Maxima se dá používat jako jednoduchá kalkulačka. Pokud počítáme celočíselně, stačí zadat např.:

(C1) 1+1;

a výstupem nám bude

(D1)                    2

Podobně i jiné operace:

(C2) 9-6/3;
(D2)                    7
(C3) 5^3-5*5;
(D3)                   100
(C4) 5!+4!;
(D4)                   144

Pokud zadáme k výpočet s neceločíselným výsledkem, Maxima ho převede na zlomek v základním tvaru.

(C5) 18/4;
                        9
(D5)                    -
                        2

Jestliže chceme dostat výsledek ve tvaru desetinného čísla, musíme zapsat za výpočet parametr numer.

(C6) 18/4,numer;
(D6)                   4.5

Úprava výrazů

Pokud zadáme algebraický výraz, nejdříve se jenom opíše, např.:

(C7) (x+5)^3;
                             3
(D7)                  (x + 5)

Pokud chceme výraz roznásobit (udělat z něj polynom), použijeme příkaz expand(výraz);. Pokud roznásobujeme nebo jinak používáme poslední příkaz, stačí místo něho napsat procento %. Pokud odkazujeme na jiný, dříve použitý příkaz, použijeme jeho název, např. C1, či D5.

(C8) expand(%);
                  3      2
(D8)             x  + 15x  + 75x + 125

Jiná je situace u lomeného výrazu, u kterého nám expand(); nepomůže. Pro zkrácení použijeme příkaz radcan(výraz);

(C9) (a^2-b^2)/(a+b);
                      2    2
                     a  - b
(D9)                 -------
                     a  + b
(C10) expand(%);
                    2       2
                   a       b
(D10)             ----- + -----
                  a + b   a + b
(C11) radcan(%);
(D11)                 a - b

Ludolfovo a Eulerovo číslo, výpočty s velkou přesností

Maxima zná Ludolfovo číslo π, které označuje %pi a Eulerovo číslo e, které označuje %e a umí je normálním způsobem používat ve výrazech a rovnicích. Pokud nezadáme parametr numer, počítá výsledky rovněž s těmito čísly.

(C12) 2*3/%pi;
                        6
(D12)                  ---
                       %pi
(C13) %, numer;
(D13)           1.909859317102744

Parametr numer počítá s přesností na 16 platných číslic. Ten samý výsledek v semilogaritmickém tvaru dostaneme použitím funkce bfloat(výraz);. Ten má primární přesnost také 16 platných číslic. Tu však můžeme měnit pomocí proměnné fpprec. Nejdříve si pomocí zadání fpprec; ověříme, že přesnost je skutečně 16 a pak ji změníme na 121:

(C14) bfloat(%e);
(D14)          2.718281828459045B0
(C15) fpprec;
(D15)                  16
(C16) fpprec: 121;
(D16)                  121
(C17) bfloat(%e);
(D17) 2.718281828459045235360287471352662497757247093699959574966967627724076#
      630353547594571382178525166427427466391932003059922B0

B0 zde vlastně znamená „krát deset na nultou“. Pokud použijeme funkci bfloat(); ve výrazu, pak se celý počítá s přesností fpprec.

Řešení lineárních rovnic

K řešení jedná rovnice slouží funkce solve(rovnice,neznámé);. K řešení soustavy lineárních rovnic slouží funkce linsolve([rovnice],[neznámá]);.

(C18) a:x+y=5;
(D18)                  y + x = 5
(C19) b:x-y=1;
(D19)                  x - y = 1
(C20) linsolve([a,b],[x,y]);
(D20)                  [x = 3, y = 2]
Remove ads

Související články

Externí odkazy

  • Obrázky, zvuky či videa k tématu Maxima na Wikimedia Commons
Pahýl
Pahýl
 Tento článek je příliš stručný nebo postrádá důležité informace.
Pomozte Wikipedii tím, že jej vhodně rozšíříte. Nevkládejte však bez oprávnění cizí texty.
Loading related searches...

Wikiwand - on

Seamless Wikipedia browsing. On steroids.

Remove ads