Hopf-Algebra

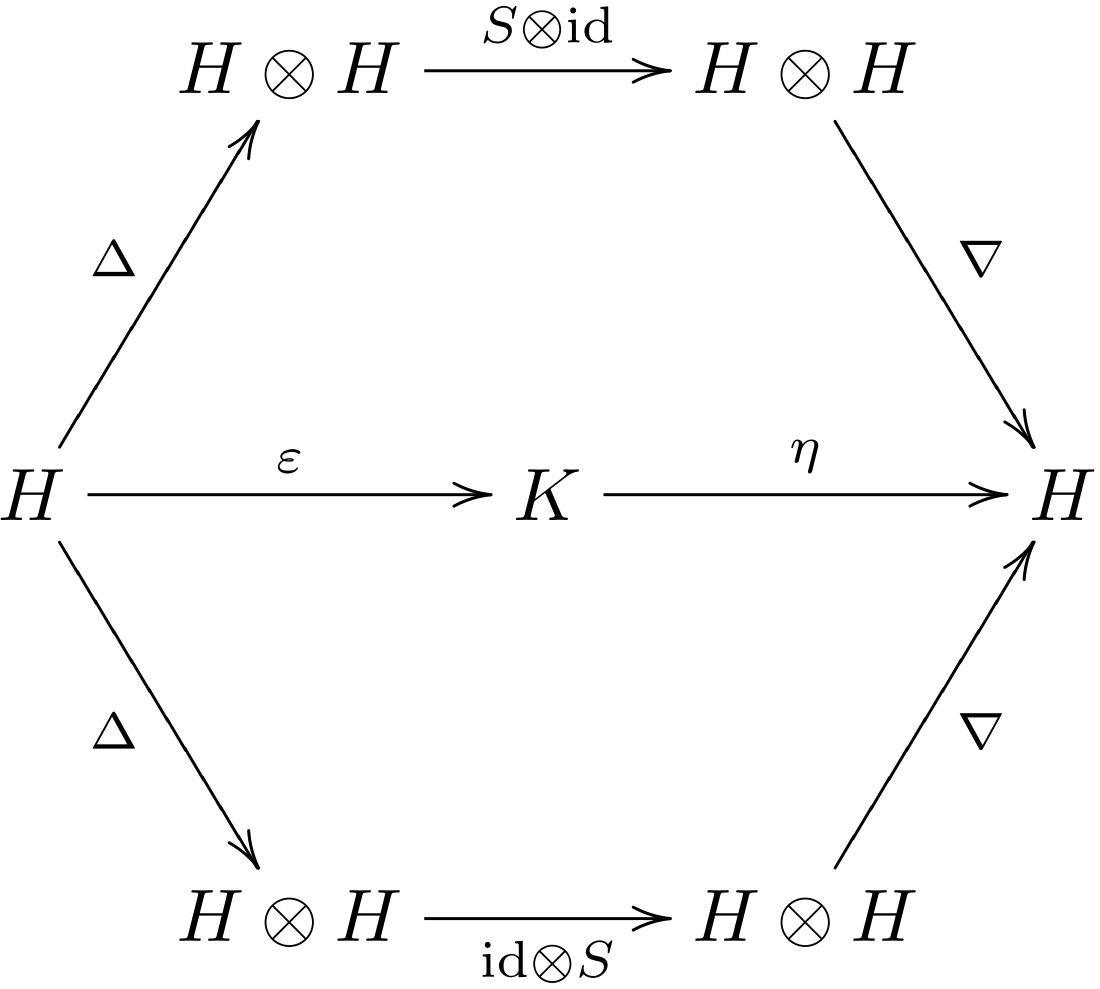
Eine Hopf-Algebra – benannt nach dem Mathematiker Heinz Hopf – ${\displaystyle H}$ über einem Körper ${\displaystyle \mathbb {K} }$ ist eine Bialgebra ${\displaystyle (H,\nabla ,\eta ,\Delta ,\epsilon )}$ mit einer ${\displaystyle \mathbb {K} }$-linearen Abbildung, der sog. „Antipode“, ${\displaystyle S\colon H\to H}$, so dass das folgende Diagramm kommutiert:

Hopfalgebra

berührt die Spezialgebiete

Mathematik Abstrakte Algebra Lineare Algebra Kommutative Algebra

ist Spezialfall von

Bialgebra

Formal in der Sweedler-Notation – benannt nach Moss Sweedler – geschrieben heißt das: ${\displaystyle S\left(c_{\left(1\right)}\right)c_{\left(2\right)}=c_{\left(1\right)}S\left(c_{\left(2\right)}\right)=\epsilon \left(c\right)1.}$

Faltung und Antipode

Sei ${\displaystyle A}$ eine Algebra und ${\displaystyle C}$ eine Koalgebra. Die ${\displaystyle \mathbb {K} }$-linearen Abbildungen von ${\displaystyle C}$ nach ${\displaystyle A}$ bilden eine Algebra mit Produkt ${\displaystyle *}$, genannt Faltung, definiert durch

${\displaystyle (f*g)(x):=f(x_{(1)})g(x_{(2)})}$.

Das neutrale Element in dieser Algebra ist ${\displaystyle \eta \circ \epsilon }$, denn

${\displaystyle (f*(\eta \circ \epsilon ))(x)=f(x_{(1)})\eta (\epsilon (x_{(2)}))=f(x_{(1)}\epsilon (x_{(2)}))\eta (1)=f(x)}$

und entsprechend auch

${\displaystyle ((\eta \circ \epsilon )*f)(x)=f(x)}$.

Für eine Bialgebra ${\displaystyle H}$ bilden die ${\displaystyle \mathbb {K} }$-linearen Abbildungen von ${\displaystyle H}$ nach ${\displaystyle H}$ auf diese Weise eine Algebra. Die Antipode ${\displaystyle S}$ ist das zur identischen Abbildung inverse Element in dieser Algebra. Das heißt

${\displaystyle S*\mathrm {id} =\eta \circ \epsilon =\mathrm {id} *S}$.

Es lässt sich zeigen, dass die Antipode einer Hopf-Algebra stets eindeutig ist, und gleichzeitig ein Antialgebrahomomorphismus und ein Anticoalgebrahomomorphismus ist. Mithilfe dieser Tatsache lässt sich der Wert der Antipode auf jedem Element der Hopf-Algebra ausrechnen, wenn die Werte der Antipode auf einem Algebraerzeugendensystem bekannt sind.

Beispiele

Gruppenalgebra

Ein Beispiel für eine Hopf-Algebra ist die Gruppenalgebra ${\displaystyle \mathbb {K} G}$. Sie wird durch

${\displaystyle \Delta (g):=g\otimes g}$ für ${\displaystyle g\in G}$

und

${\displaystyle \epsilon (g):=1}$ für ${\displaystyle g\in G}$

zu einer Bialgebra, die Antipode

${\displaystyle S(g):=g^{-1}}$ für ${\displaystyle g\in G}$

macht sie zu einer Hopf-Algebra.

Universelle einhüllende Algebra

Die universelle einhüllende Algebra ${\displaystyle \mathrm {U} ({\mathfrak {g}})}$ einer Lie-Algebra ${\displaystyle {\mathfrak {g}}}$ ist auf natürliche Weise eine Hopfalgebra. Für ein Element ${\displaystyle x\in {\mathfrak {g}}}$ ist das Koprodukt durch

${\displaystyle \Delta (x):=1\otimes x+x\otimes 1}$

und die Koeins durch

${\displaystyle \epsilon (x):=0}$

definiert.

${\displaystyle S(x):=-x}$

definiert die Antipode.

Gruppenartige und primitive Elemente

Ein Element ${\displaystyle g}$ einer Hopfalgebra heißt „gruppenartig“, wenn ${\displaystyle \Delta (g)=g\otimes g}$ und ${\displaystyle \epsilon (g)=1}$. Für die Antipode gilt dann ${\displaystyle S(g)=g^{-1}}$.

Ein Element ${\displaystyle x}$ heißt „primitiv“, wenn ${\displaystyle \Delta (x)=1\otimes x+x\otimes 1}$. Daraus folgt, dass ${\displaystyle \epsilon (x)=0}$ und ${\displaystyle S(x)=-x}$.

Ein Element ${\displaystyle x}$ heißt „schiefprimitiv“, wenn ${\displaystyle \Delta (x)=g\otimes x+x\otimes h}$ mit gruppenähnlichen Elementen ${\displaystyle g}$ und ${\displaystyle h}$. Daraus folgt, dass ${\displaystyle \epsilon (x)=0}$ und ${\displaystyle S(x)=-g^{-1}xh^{-1}}$.

Literatur

• Christian Kassel: Quantum Groups (= Graduate Texts in Mathematics. 155). Springer, New York NY u. a. 1995, ISBN 0-387-94370-6.
• Moss E. Sweedler: Hopf algebras. Benjamin, New York NY 1969.