Immersion (Mathematik)

In der Differentialtopologie versteht man unter einer Immersion eine glatte Abbildung ${\displaystyle F\colon M\rightarrow N}$ zwischen Mannigfaltigkeiten ${\displaystyle M}$ und ${\displaystyle N}$, wenn der Pushforward ${\displaystyle F_{\ast p}\colon T_{p}M\to T_{F(p)}N}$ dieser Abbildung an jedem Punkt ${\displaystyle p\in M}$ injektiv ist. Ist darüber hinaus ${\displaystyle F}$ eine topologische Einbettung, so spricht man von einer (glatten) Einbettung. In diesem Fall ist das Bild der Abbildung eine zu ${\displaystyle M}$ diffeomorphe Untermannigfaltigkeit von ${\displaystyle N.}$

Eine nicht injektive Immersion: R → R², t ↦ (t² − 1, t · (t² − 1))

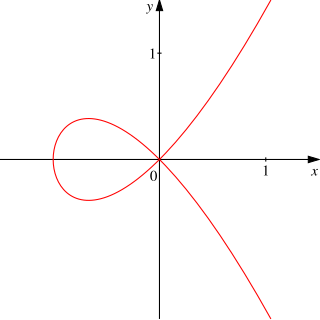
Die Eigenschaften des Bildes im allgemeinen Fall werden im Eintrag Immersierte Mannigfaltigkeit beschrieben.

Immersion im euklidischen Raum

Liegt der Spezialfall ${\displaystyle F:\mathbb {R} ^{m}\rightarrow \mathbb {R} ^{n}}$ einer Abbildung zwischen euklidischen Räumen vor, dann stellt ${\displaystyle F_{\ast }:T_{p}\mathbb {R} ^{m}\rightarrow T_{F(p)}\mathbb {R} ^{n}}$ nichts anderes als die totale Ableitung bzw. die Jacobi-Matrix ${\displaystyle DF(p)\colon \mathbb {R} ^{m}\rightarrow \mathbb {R} ^{n}}$ dar, wobei der euklidische Raum in natürlicher Weise mit seinem Tangentialraum und eine lineare Abbildung mit einer Matrix identifiziert werden.

Immersion in Mannigfaltigkeiten

Allgemein ist eine differenzierbare Abbildung ${\displaystyle F:M\rightarrow N}$ genau dann eine Immersion, wenn für alle ${\displaystyle p\in M}$ der Rang der linearen Abbildung ${\displaystyle F_{\ast }}$ gleich der Dimension der Mannigfaltigkeit ${\displaystyle M}$ ist, also gilt

${\displaystyle \operatorname {rang} F_{p}=\dim(\operatorname {Bild} (F_{\ast p}))=\dim M.}$

Reguläre Homotopie

Zwei Immersionen ${\displaystyle F_{0},F_{1}\colon M\to N}$ heißen regulär homotop, wenn es eine Homotopie ${\displaystyle F\colon M\times [0,1]\to N}$ gibt mit ${\displaystyle F(m,0)=F_{0}(m)}$ und ${\displaystyle F(m,1)=F_{1}(m)}$ für alle ${\displaystyle m\in M}$, so dass für jedes ${\displaystyle t\in \left[0,1\right]}$ die Abbildung

${\displaystyle F_{t}\colon \left\{{\begin{aligned}M&\to N\\m&\mapsto F(m,t)\end{aligned}}\right.}$

wieder eine Immersion ist.

Mit den regulären Homotopieklassen von Immersionen beschäftigt sich die Hirsch-Smale-Theorie.

Siehe auch

• Submersion

Literatur

• John M. Lee: Introduction to Smooth Manifolds (= Graduate Texts in Mathematics 218). Springer-Verlag, New York NY u. a. 2003, ISBN 0-387-95448-1.