Umfang (Geometrie)

Der Umfang einer ebenen Figur, die durch eine Linie begrenzt ist, bezeichnet die Länge ihrer Begrenzungslinie.

Umfang des Kreises:
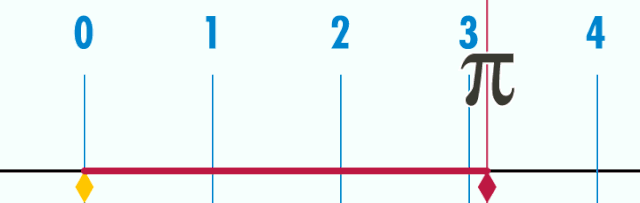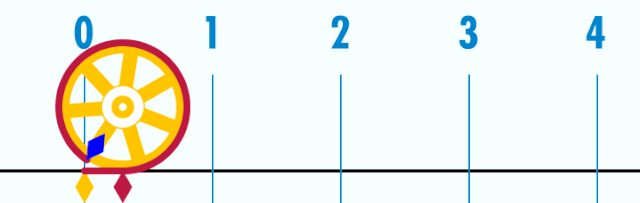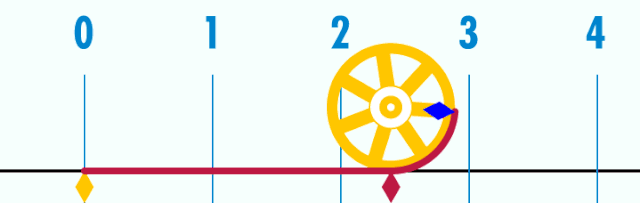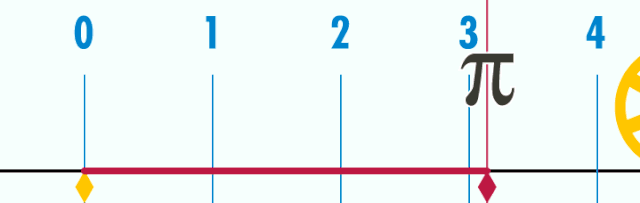
U = d·π (hier ist d = 1)

Umfang des Rechtecks:
U = 2·a + 2·b = 2·(a + b)

Die Formel für den Kreisumfang lautet:

${\displaystyle U=\pi \,d=2\pi \,r}$

• ${\displaystyle U}$ steht dabei für den Umfang,
• ${\displaystyle r}$ für den Radius des Kreises,
• ${\displaystyle \pi }$ für die Kreiszahl mit dem Wert 3,14159265… und
• ${\displaystyle d}$ für den Kreisdurchmesser.

Der Umfang eines Vielecks ist die Summe seiner Seitenlängen.

Herzkurve ${\displaystyle \gamma \colon [0,2\pi ]\rightarrow \mathbb {R} ^{2}}$
(Zeichnung mit ${\displaystyle a=1}$)
${\displaystyle x(t)=2a\cos(t)(1+\cos(t))}$
${\displaystyle y(t)=2a\sin(t)(1+\cos(t))}$
${\displaystyle U=\int \limits _{0}^{2\pi }{\sqrt {x'(t)^{2}+y'(t)^{2}}}\,\mathrm {d} t=16a}$

Wird die Begrenzungslinie der Figur durch eine geschlossene stückweise glatte Parameterkurve ${\displaystyle \gamma \colon [a,b]\rightarrow \mathbb {R} ^{2}}$ beschrieben mit

${\displaystyle \gamma (t)={\begin{pmatrix}x(t)\\y(t)\end{pmatrix}}}$,

so lässt sich ihr Umfang ${\displaystyle U}$ über das folgende Integral berechnen:

${\displaystyle U=\int \limits _{a}^{b}{\sqrt {x'(t)^{2}+y'(t)^{2}}}\,\mathrm {d} t}$. (siehe Länge (Mathematik))

Literatur

• Karl Barth: Die technischen Hilfswissenschaften: Mathematik, Geometrie und Chemie. Oldenbourg, S. 95–96

Weblinks

Wiktionary: Umfang – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Eric W. Weisstein: Perimeter. In: MathWorld (englisch).
• Umfang und Flächen elementarer Figuren