Νόμος των συνημιτόνων

Στην τριγωνομετρία, ο νόμος των συνημιτόνων αποτελεί μια γενίκευση του πυθαγόρειου θεωρήματος, που συνδέει το μήκος των τριών πλευρών ενός τριγώνου και το συνημίτονο μίας εκ των γωνιών. Πιο συγκεκριμένα, σε ένα τρίγωνο ${\displaystyle {\rm {AB\Gamma }}}$ με μήκη πλευρών ${\displaystyle \alpha ,\beta ,\gamma }$ δίνει τις εξής σχέσεις:

${\displaystyle \gamma ^{2}=\alpha ^{2}+\beta ^{2}-2\alpha \beta \cdot \cos {\rm {\Gamma }}}$,

${\displaystyle \alpha ^{2}=\beta ^{2}+\gamma ^{2}-2\beta \gamma \cdot \cos {\rm {A}}}$,

${\displaystyle \beta ^{2}=\gamma ^{2}+\alpha ^{2}-2\gamma \alpha \cdot \cos {\rm {B}}}$.

Σχήμα 1: Ένα τρίγωνο ${\displaystyle {\rm {AB\Gamma }}}$ με μήκη πλευρών ${\displaystyle \alpha ,\beta ,\gamma }$.

Ο νόμος των συνημιτόνων είναι μία από τις βασικές σχέσεις που χρησιμοποιείται για να "λύσει ένα τρίγωνο". Συγκεκριμένα, (i) δοσμένων των μηκών δύο πλευρών ενός τριγώνου και της περιεχόμενης τους γωνίας, μπορούμε να υπολογίσουμε το μήκος της τρίτης πλευράς και (ii) δοσμένων των μηκών των τριών πλευρών μπορούμε να υπολογίσουμε το μέγεθος των γωνιών του (δείτε παρακάτω).

Μία απλή εφαρμογή

Έστω ότι θέλουμε να χτίσουμε ένα τούνελ σε ένα βουνό μεταξύ δύο σημείων ${\displaystyle {\rm {A}}}$ και ${\displaystyle {\rm {B}}}$. Για να υπολογίσουμε το κόστος κατασκευής πρέπει να υπολογίσουμε το μήκος του τούνελ, δηλαδή την απόσταση μεταξύ του ${\displaystyle {\rm {A}}}$ και ${\displaystyle {\rm {B}}}$. Δεν μπορούμε να την μετρήσουμε κατευθείαν καθώς υπάρχει το βουνό μεταξύ τους.

Αυτό που μπορούμε να κάνουμε είναι να σταθούμε σε ένα σημείο ${\displaystyle {\rm {\Gamma }}}$ και να μετρήσουμε τις αποστάσεις προς το ${\displaystyle {\rm {A}}}$ και το ${\displaystyle {\rm {B}}}$ (διαλέγοντας το ${\displaystyle {\rm {\Gamma }}}$ ώστε να μην μεσολαβεί βουνό μεταξύ τους) και επίσης μετράμε την γωνία ${\displaystyle {\hat {\rm {\Gamma }}}}$. Αυτές οι πληροφορίες είναι αρκετές για να βρούμε την απόσταση μεταξύ των ${\displaystyle {\rm {A}}}$ και ${\displaystyle {\rm {B}}}$, χρησιμοποιώντας τον νόμο των συνημιτόνων, δηλαδή

${\displaystyle {\rm {AB}}=\gamma ={\sqrt {\alpha ^{2}+\beta ^{2}-2\alpha \beta \cdot \cos {\rm {\Gamma }}}}}$,

όπου όλα τα στοιχεία του δεξιού μέλους είναι γνωστά.

Μήκος τούνελ

Θέλουμε να βρούμε την απόσταση μεταξύ ${\displaystyle {\rm {A}}}$ και ${\displaystyle {\rm {B}}}$.

Οι μετρήσεις που παίρνουμε από το σημείο ${\displaystyle {\rm {\Gamma }}}$.

Ιστορικά

Σχήμα 2: Τρίγωνο ${\displaystyle {\rm {AB\Gamma }}}$ με ύψος ${\displaystyle {\rm {BH}}}$.

Τα Στοιχεία του Ευκλείδη, που χρονολογούνται από τον 3ο αιώνα π.Χ., περιείχαν ήδη μια γεωμετρική προσέγγιση της γενίκευσης του πυθαγόρειου θεωρήματος. Συγκεκριμένα: οι προτάσεις 12 και 13 του 2ου βιβλίου αντιμετωπίζουν τις περιπτώσεις ενός αμβλυγώνιου και ενός οξυγώνιου αντίστοιχα. Η απουσία τριγωνομετρικής και αλγεβρικής ερμηνείας όμως απαιτούσε επαναδιατύπωση του θεωρήματος. Συγκεκριμένα η πρόταση 12:^[1]

Στα αμβλυγώνια τρίγωνα το τετράγωνο της πλευράς της κείμενης απέναντι της αμβλείας γωνίας, είναι μεγαλύτερο των τετραγώνων των πλευρών που την περιέχουν, κατά το διπλάσιο ορθογώνιο που περιέχεται μεταξύ της μιας πλευράς της αμβλείας γωνίας, του ύψους που πίπτει σε αυτήν και της ευθείας που ενώνει την αμβλεία με το ύψος.

Έστω ${\displaystyle {\rm {AB\Gamma }}}$ αμβλυγώνιο τρίγωνο με το ύψος του ${\displaystyle {\rm {BH}}}$ (Σχήμα 2), μπορούμε με τις σύγχρονες μεθόδους να συνοψίσουμε την πρόταση ως εξής:

${\displaystyle {\rm {AB}}^{2}={\rm {\Gamma A}}^{2}+{\rm {\Gamma B}}^{2}+2\cdot {\rm {\Gamma A}}\cdot {\rm {\Gamma H}}}$.

Η αραβο-μουσουλμανική τριγωνομετρία τον Μεσαίωνα συνείσφερε στη βελτίωση του θεωρήματος: ο αστρονόμος και μαθηματικός Αλ-Μπατάνι γενίκευσε την πρόταση του Ευκλείδη στην σφαιρική γεωμετρία τον 10ο αιώνα, κάτι το οποίο επέτρεψε τον υπολογισμό των γωνιακών αποστάσεων μεταξύ αστέρων. Εκείνη την περίοδο συντάχθηκαν και οι πρώτοι τριγωνομετρικοί πίνακες για το ημίτονο και το συνημίτονο, επιτρέποντας στον Άλ-Κασί, μαθηματικό της σχολής της Σαμαρκάνδης, να μορφοποιήσει το θεώρημα ώστε να το χρησιμοποιήσει στον τριγωνισμό, τον 15ο αιώνα. Αργότερα, το θεώρημα έγινε γνωστό στη δύση από τον Φρανσουά Βιέτ, ο οποίος, όπως φαίνεται, το επινοήθηκε^[2].
Στις αρχές του 19ου αιώνα το θεώρημα ερμηνεύτηκε σύμφωνα με τη σύγχρονη άλγεβρα και έγινε γνωστό με τη σημερινή του ονομασία: νόμος των συνημιτόνων.

Το θεώρημα και οι εφαρμογές του

Σχήμα 3: Χρησιμοποιώντας το θεώρημα για τον υπολογισμό άγνωστης πλευράς ή γωνίας.

Το Πυθαγόρειο θεώρημα είναι μία ειδική περίπτωση του νόμου των συνημιτόνων

Η γωνία ${\displaystyle {\hat {\rm {\Gamma }}}}$ έχει συνημίτονο ίσο με μηδέν (${\displaystyle \cos {\rm {\Gamma }}=0}$) αν και μόνο αν ${\displaystyle \gamma ^{2}=\alpha ^{2}+\beta ^{2}}$.

Το θεώρημα χρησιμοποιείται στον τριγωνισμό (Σχήμα 3) για να "λύσει ένα τρίγωνο", δηλαδή να προσδιορίσει

• μια πλευρά ενός τριγώνου γνωρίζοντας την απέναντί της γωνία και τις παρακείμενες πλευρές:

${\displaystyle \gamma ={\sqrt {\alpha ^{2}+\beta ^{2}-2\alpha \beta \cos {\rm {\Gamma }}}}}$,

• μια γωνία ενός τριγώνου γνωρίζοντας τις τρεις πλευρές του:

${\displaystyle {\hat {\Gamma }}=\arccos \left({\dfrac {\alpha ^{2}+\beta ^{2}-\gamma ^{2}}{2\alpha \beta }}\right)}$.

Αυτοί οι τύποι είναι αριθμητικά ασταθείς σε περίπτωση που το ${\displaystyle \gamma }$ είναι μικρότερο του ${\displaystyle \beta }$ και του ${\displaystyle \alpha }$, ή ισοδύναμα όταν ${\displaystyle \gamma }$ είναι μικρότερο του 1.

Στην περίπτωση των ομοίων τριγώνων ${\displaystyle {\rm {AB\Gamma }}}$ και ${\displaystyle {\rm {A'B'\Gamma '}}}$ ισχύει το εξής:

${\displaystyle \gamma \gamma '=\alpha \alpha '+\beta \beta '-(\alpha \beta '+\alpha '\beta )\cos {\rm {\Gamma }}}$.

Αποδείξεις

Ακριβώς όπως το Πυθαγόρειο θεώρημα, το θεώρημα αυτό έχει πολλές αποδείξεις, χρησιμοποιώντας κάποιες ιδιότητες του Ευκλείδη ή του Άλ-Κασί, χρησιμοποιώντας τριγωνομετρικές ιδιότητες ή ιδιότητες που σχετίζονται με τον κύκλο. Τέλος, το θεώρημα μπορεί να θεωρηθεί εφαρμογή των ιδιοτήτων του εσωτερικού γινομένου.

Απόδειξη του Ευκλείδη

Σχήμα 4: Απόδειξη του νόμου των συνημιτόνων για αμβλυγώνιο, κατά τον Ευκλείδη. Η απόδειξη του Ευκλείδη για τις προτάσεις 12 και 13 βασίζεται στο Πυθαγόρειο θεώρημα και περιλαμβάνει το ύψος ${\displaystyle {\rm {BH}}}$ του τριγώνου ${\displaystyle {\rm {AB\Gamma }}}$. Για το αμβλυγώνιο (πρόταση 12) σχημάτισε ένα τετράγωνο στην πλευρά ${\displaystyle {\rm {AH}}}$ του τριγώνου ${\displaystyle {\rm {AHB}}}$: ${\displaystyle {\rm {\Gamma H}}^{2}+{\rm {\Gamma A}}^{2}+2\cdot {\rm {\Gamma H}}\cdot {\rm {A\Gamma }}={\rm {AH}}^{2}}$. Προσέθεσε κατά μέλη το τετράγωνο της πλευράς ${\displaystyle {\rm {HB}}}$ ${\displaystyle {\rm {HB^{2}+\Gamma H^{2}+\Gamma A^{2}+2\cdot \Gamma H\times A\Gamma =AH^{2}+HB^{2}}}}$, και χρησιμοποίησε το Πυθαγόρειο θεώρημα στο ορθογώνιο τρίγωνο ${\displaystyle {\rm {HB\Gamma }}}$ ${\displaystyle {\rm {\Gamma B^{2}+\Gamma A^{2}+2\cdot \Gamma H\cdot \Gamma A=AB^{2}}}}$ Παρόμοια είναι η απόδειξη για όταν η ${\displaystyle {\hat {\rm {\Gamma }}}}$ είναι οξεία.[3]

Απόδειξη του Άλ-Κασί

Σχήμα 4: Απόδειξη του νόμου των συνημιτόνων για οξυγώνιο τρίγωνο, κατά τον Άλ-Κασί. Στο βιβλίο του Κλειδί της Αριθμητικής το 1429[4] ο Άλ-Κασί γενίκευσε το Πυθαγόρειο θεώρημα και εισήγαγε στην ισότητα την τριγωνομετρία. Σε ένα οξυγώνιο τρίγωνο ${\displaystyle {\rm {AB\Gamma }}}$ σχεδίασε τα εξωτερικά τετράγωνα των πλευρών του και θεώρησε τα ορθογώνια που δημιουργούνται από τις προεκτάσεις των υψών του ${\displaystyle {\rm {AB\Gamma }}}$. Στο Σχήμα 4 απέδειξε ότι τα ορθογώνια ίσου χρώματος έχουν ίσο εμβαδό. Θα αποδείξουμε τώρα ότι ${\displaystyle {\rm {E}}_{\rm {AE\Xi K}}={\rm {E}}_{\rm {AZO\Lambda }}}$, δείχνοντας ότι ${\displaystyle {\rm {E}}_{\rm {KAE}}={\rm {E}}_{\rm {AZ\Lambda }}}$. Οι ισότητες μεταξύ των υπόλοιπων ορθογωνίων προκύποτυν ανάλογα. Τα τρίγωνα ${\displaystyle {\rm {KAE}}}$ και ${\displaystyle {\rm {KAB}}}$ έχουν κοινή βάση (την ${\displaystyle {\rm {KA}}}$) και ίσο ύψος (το ${\displaystyle {\rm {AE}}}$), άρα ${\displaystyle {\rm {E}}_{\rm {KAE}}={\rm {E}}_{\rm {AZ\Lambda }}}$. Τα τρίγωνα ${\displaystyle {\rm {KAB}}}$ και ${\displaystyle {\rm {\Gamma A\Lambda }}}$ έχουν δύο πλευρές ίσες (${\displaystyle {\rm {KA=A\Gamma }}}$ και ${\displaystyle {\rm {AB=A\Lambda }}}$) και την περιεχόμενη γωνία τους ίση (${\displaystyle {\rm {{\widehat {KAB}}=90^{\circ }+{\hat {A}}={\widehat {\Gamma A\Lambda }}}}}$), άρα ${\displaystyle {\rm {E}}_{\rm {KAB}}={\rm {E}}_{\rm {AZ\Lambda }}}$. Τα τρίγωνα ${\displaystyle {\rm {\Gamma A\Lambda }}}$ και ${\displaystyle {\rm {ZA\Lambda }}}$ έχουν κοινή βάση (την ${\displaystyle {\rm {A\Lambda }}}$) και ίσο ύψος (το ${\displaystyle {\rm {\Lambda Z}}}$), άρα ${\displaystyle {\rm {E}}_{\rm {\Gamma A\Lambda }}={\rm {E}}_{\rm {ZA\lambda }}}$. Στο ορθογώνιο τρίγωνο ${\displaystyle {\rm {EB\Gamma }}}$, έχουμε ότι ${\displaystyle {\rm {\Gamma E}}={\rm {B\Gamma }}\cdot \cos {\rm {\Gamma }}}$, και στο ορθογώνιο ${\displaystyle {\rm {\Delta A\Gamma }}}$, ισχύει ότι ${\displaystyle {\rm {\Gamma \Delta }}={\rm {A\Gamma }}\cdot \cos {\rm {\Gamma }}}$. Επομένως, το εμβαδόν των πράσινων ορθογωνίων είναι ${\displaystyle {\rm {E}}_{\rm {\Gamma E\Xi I}}={\rm {E}}_{\rm {\Gamma \Delta N\Theta }}={\rm {\Gamma A}}\cdot {\rm {\Gamma B}}\cdot \cos {\hat {\rm {\Gamma }}}}$. Αθροίζοντας τα εμβαδά των τετραγώνων, καταλήγουμε ότι ${\displaystyle {\rm {\Gamma A}}^{2}+{\rm {\Gamma B}}^{2}={\rm {AB}}^{2}+2\cdot {\rm {\Gamma B}}\cdot {\rm {\Gamma A}}\cdot \cos {\rm {\Gamma }}}$. Παρόμοια είναι και η απόδειξη για τα αμβλυγώνια τρίγωνα, αλλά εκεί πρέπει να αφαιρεθούν εμβαδά σχημάτων.

Απόδειξη με σύγκριση εμβαδών

Σχήμα 6α: Απόδειξη με σύγκριση εμβαδών για οξείες γωνίες Σχήμα 6β: Απόδειξη με σύγκριση εμβαδών για αμβλύες γωνίες Αρκετές αποδείξεις χρησιμοποιούν τον υπολογισμό εμβαδών. Θα πρέπει να σημειωθεί, λοιπόν, πως: ${\displaystyle a^{2}}$, ${\displaystyle b^{2}}$ και ${\displaystyle c^{2}}$ είναι τα εμβαδά των τετραγώνων των αντίστοιχων πλευρών ${\displaystyle a}$, ${\displaystyle b}$ και ${\displaystyle c}$ ; ${\displaystyle ab|\cos \gamma |}$ είναι αυτό του παραλληλογράμου με πλευρές ${\displaystyle a}$ και ${\displaystyle b}$ σχηματίζοντας μια γωνία ${\displaystyle \pi /2-\gamma }$, η αλλαγή του προσήμου του ${\displaystyle \cos \gamma }$ γίνεται όταν η γωνία ${\displaystyle \gamma }$ γίνεται αμβλύα. 'Όπως φαίνεται επιβάλεται η μελέτη κατά περίπτωση. Στο σχήμα 6α, το επτάγωνο χωρίζεται με δύο διαφορετικούς τρόπους για να αποδείξει το θεώρημα για μια οξεία γωνία: σε κόκκινο: τα εμβαδά ${\displaystyle a^{2}}$, ${\displaystyle b^{2}}$ αριστερά, και τα εμβαδά ${\displaystyle 2ab\cos \gamma }$ και ${\displaystyle c^{2}}$ δεξιά. σε μπλέ: το τρίγωνο ABC, στα δεξιά όπως και στα αριστερά. σε γκρί: κάποια τρίγωνα συμπληρωματικά, πανομοιότυπα με το τρίγωνο ABC και σε ίδιο αριθμό στα δύο σχήματα. Οι ισότητες των εμβαδών στα αριστερά και δεξιά δίνουν: ${\displaystyle \,a^{2}+b^{2}=c^{2}+2ab\cos \gamma }$. Στο σχήμα 6β, το εξάγωνο χωρίζεται με δύο διαφορετικούς τρόπους για να αποδείξει το θεώρημα για μια αμβλύα γωνία: σε κόκκινο: τα εμβαδά ${\displaystyle a^{2}}$, ${\displaystyle b^{2}}$ και ${\displaystyle -2ab\cos \gamma }$ αριστερά, και το εμβαδό ${\displaystyle c^{2}}$ δεξιά. σε μπλέ: δύο φρές το τρίγωνο ABC, στα δεξιά όπως και στα αριστερά. Οι ισότητες των εμβαδών στα αριστερά και δεξιά δίνουν: ${\displaystyle \,a^{2}+b^{2}-2ab\cos \gamma =c^{2}}$. Για να αποδείξουμε πως τα δύο σχήματα είναι ίσα, χρησιμοποιούμε τα κριτήρια ισότητας τριγώνων[5].

Απόδειξη με το Πυθαγόρειο θεώρημα

Σχήμα 7: Απόδειξη χρησιμοποιώντας τριγωνομετρικές σχέσεις. Το σχήμα 7 δείχνει πως αποδυκνείεται ο νόμος των συνημιτόνων για ένα οξυγώνιο, χρησιμοποιώντας το Πυθαγόρειο θεώρημα σε ένα περιεχόμενο ορθογώνιο τρίγωνο, σχηματιζόμενο από το ύψος του οξυγωνίου.[6] Το τελευταίο βήμα που δεν εμφανίζεται στην εικόνα είναι πως το Πυθαγόρειο θεώρημα ισχύει για το ορθογώνιο, με υποτείνουσα την πλευρά ${\displaystyle \gamma }$. ${\displaystyle \gamma ^{2}=(\beta \sin {\rm {\Gamma }})^{2}+(\alpha -\beta \cos {\rm {\Gamma }})^{2}}$. Η απόδειξη είναι παρόμοια για τα αμβλυγώνια.

Απόδειξη με ιδιότητες του κύκλου

Σχήμα 8: Απόδειξη χρησιμοποιώντας την γεωμετρία του κύκλου. Έστω ο κύκλος με κέντρο ${\displaystyle {\rm {B}}}$ και ακτίνα ${\displaystyle {\rm {B\Gamma }}}$, ο οποίος τέμνει την πλευρά ${\displaystyle {\rm {A\Gamma }}}$ στο ${\displaystyle {\rm {\Gamma }}}$ και το ${\displaystyle {\rm {K}}}$ κατ'επέκταση. Από το δύναμη σημείου ως προς κύκλο: ${\displaystyle \mathrm {AB} ^{2}-\mathrm {B\Gamma } ^{2}={\overline {\mathrm {A\Gamma } }}\cdot {\overline {\mathrm {AK} }}={\overline {\mathrm {A\Gamma } }}\cdot ({\overline {\mathrm {A\Gamma } }}+{\overline {\mathrm {\Gamma K} }})}$ όπου ${\displaystyle \gamma ^{2}-\alpha ^{2}=\beta \cdot (b-2a\cos {\rm {\Gamma }})}$. Εδώ δεν χρειάζεται να αποδείξουμε κατά περιπτώσεις. Πράγματι οι αλγεβρικές ιδιότητες επιτρέπουν την παράλληλη απόδειξη για αμβλεία (${\displaystyle {\overline {\mathrm {\Gamma K} }}>0}$) και οξεία γωνία (${\displaystyle {\overline {\mathrm {\Gamma K} }}<0}$). Ο Νικόλαος Κοπέρνικος στο βιβλίο του Περί των Περιστροφών των Ουρανίων Σφαιρών φαίνεται να χρησιμοποίησε το θεώρημα των τεμνόμενων χορδών για να καθορίσει όλες τις γωνίες ενός τριγώνου, με γνωστά μήκη πλευρών.[7][8] Χρησιμοποίησε δύο αλγόριθμους, στον έναν χρησιμοποίησε το γενικευμένο Πυθαγόρειο θεώρημα (όπως διατυπώθηκε κατά τον Ευκλείδη) και στον άλλον χρησιμοποίησε το θεώρημα των τεμνόμενων χορδών. Έτσι, με ένα τρόπο ανάλογο με αυτόν που δείχνει το σχήμα, θεώρησε ότι ${\displaystyle \alpha }$ και ${\displaystyle \gamma }$ είναι γνωστά, από το θεώρημα των τεμνόμενων χορδών το ${\displaystyle {\rm {A}}}$ είναι γνωστό το ${\displaystyle \gamma ^{2}-\alpha ^{2}}$. Καταλήγει στο συμπέρασμα ότι, επειδή το ${\displaystyle \beta }$ είναι γνωστό, η ${\displaystyle {\rm {AK}}}$ είναι γνωστή ${\displaystyle {\rm {AK}}\cdot \beta =\gamma ^{2}-\alpha ^{2}}$ έτσι ${\displaystyle {\rm {AK}}={\frac {\gamma ^{2}-\alpha ^{2}}{\beta }}}$ Επειδή ${\displaystyle {\rm {AK}}}$ είναι γνωστή, έτσι ${\displaystyle \Gamma K}$ είναι γνωστή. από το σχήμα ${\displaystyle {\rm {\Gamma K}}={\rm {AK}}-\beta ={\frac {\gamma ^{2}-\alpha ^{2}-\beta ^{2}}{\beta }}}$ Τέλος, αφού ${\displaystyle {\rm {\Gamma K}}}$ είναι γνωστή, η γωνία ${\displaystyle {\widehat {K\Gamma B}}}$ είναι γνωστή ${\displaystyle \cos {\widehat {\rm {K\Gamma B}}}={\frac {\rm {\Gamma K}}{2\alpha }}={\frac {\gamma ^{2}-\alpha ^{2}-\beta ^{2}}{2\alpha \beta }}}$ Και εφ'όσον η γωνία ${\displaystyle {\widehat {\rm {K\Gamma B}}}}$ είναι γνωστή, ισχύει το ίδιο για την γωνία ${\displaystyle {\widehat {\rm {A\Gamma B}}}}$. Έτσι βρίσκουμε τον νόμο των συνημιτόνων ${\displaystyle \cos {\hat {\rm {\Gamma }}}={\frac {\alpha ^{2}+\beta ^{2}-\gamma ^{2}}{2\alpha \beta }}}$. Μη χρησιμοποιώντας αλγεβρικά μέτρα ο Νικόλαος Κοπέρνικος παρουσίασε δύο περιπτώσεις, για την αμβλεία και την οξεία γωνία, εργάστηκε πάνω σε έναν κύκλο του οποίου η ακτίνα αντιστοιχούσε στην μικρότερη πλευρά των τριγώνων και δεν κατέληξε σε τύπο αλλά σε αλγόριθμο υπολογισμού. Ο Νόμος των Συνημιτόνων αποδείχθηκε με παρόμοιο τρόπο από τον Βαρθολομαίο Πιτίσκο[9].

Απόδειξη με το εσωτερικό γινόμενο

Χρησιμοποιώντας διανύσματα και πιο συγκεκριμένα το εσωτερικό γινόμενο[10], είναι δυνατόν να αποδείξουμε το θεώρημα σε μερικές γραμμές: ${\displaystyle {\begin{aligned}c^{2}&=\lVert {\overrightarrow {\mathrm {AB} }}\lVert ^{2}\\&=\lVert {\overrightarrow {\mathrm {\Gamma B} }}-{\overrightarrow {\mathrm {\Gamma A} }}\lVert ^{2}\\&=\lVert {\overrightarrow {\mathrm {\Gamma B} }}\lVert ^{2}-2\cdot {\overrightarrow {\mathrm {\Gamma B} }}\cdot {\overrightarrow {\mathrm {\Gamma A} }}+\lVert {\overrightarrow {\mathrm {\Gamma A} }}\lVert ^{2}\\&=\mathrm {\Gamma B} ^{2}-2\cdot \left|\mathrm {\Gamma B} \right|\cdot \left|\mathrm {\Gamma A} \right|\cos {\widehat {\mathrm {A\Gamma B} }}+\mathrm {\Gamma A} ^{2}\\&=\alpha ^{2}+\beta ^{2}-2\alpha \beta \cos {\hat {\rm {\Gamma }}}.\end{aligned}}}$

Γενίκευση σε μη Ευκλείδειες γεωμετρίες

Για μια μη Ευκλείδεια επιφάνεια, καμπυλότητας Κ και ακτίνα καμπυλότητας R, ισχύει:

${\displaystyle \,R=1/{\sqrt {|K|}}}$.

Ορίζουμε τις μειωμένες διαστάσεις του τριγώνου:

${\displaystyle \,a=BC/R}$,

${\displaystyle \,b=AC/R}$,

${\displaystyle \,c=AB/R}$.

Στην περίπτωση σφαιρικού τριγώνου, a, b και c αντιστοιχούν στη γωνιακή μέτρηση μεγάλων τμημάτων τόξου [BC], [CA] και [ΑΒ] (σχήμα 7)

Σφαιρική γεωμετρία

Σχήμα 9: οι μειωμένες διαστάσεις τριγώνου και οι γωνίες α,β και γ

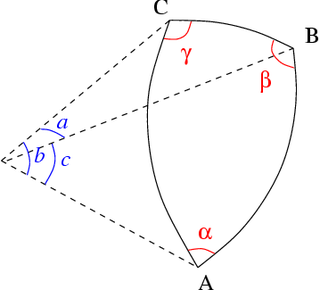
Σε ένα σφαιρικό τρίγωνο ο νόμος των συνημιτόνων ερμηνεύεται ως εξής^[11]:

${\displaystyle \cos c=\cos a\cos b+\sin a\sin b\cos \gamma }$.

Όταν η ακτίνα καμπυλότητας είναι μεγάλη σε σύγκριση με τις διαστάσεις του τριγώνου, δηλαδή όταν

${\displaystyle a\ll 1,b\ll 1,c\ll 1}$,

αυτή η έκφραση απλοποιείται για να δώσει την Ευκλείδεια εκδοχή. Για να το δείξουμε χρησιμοποιούμε:

${\displaystyle \,\sin a=a+O(a^{3}),}$

${\displaystyle \,\cos a=1-a^{2}/2+O(a^{3}).}$

Υπάρχει μια παρόμοια ταυτότητα που συνδέει και τις τρεις γωνίες:

${\displaystyle \cos \gamma =-\cos \alpha \,\cos \beta +\sin \alpha \,\sin \beta \,\cos c}$

Υπερβολική γεωμετρία

Σε ένα υπερβολικό τρίγωνο:

${\displaystyle \cosh c=\cosh a\cosh b-\sinh a\sinh b\cos \gamma }$.

Όταν η ακτίνα της καμπυλότητας γίνεται πολύ μεγάλη σε σύγκριση με το μέγεθος του τριγώνου:

${\displaystyle \sinh a=a+O(a^{3})}$,

${\displaystyle \cosh a=1+a^{2}/2+O(a^{3})}$.

Γενίκευση σε Ευκλείδειους Χώρους

Σχήμα 10: Τετράεδρο: επιφάνειες και δίεδρες γωνίες

Θεωρώ ένα τετράεδρο A₁A₂A₃A₄ σε έναν Ευκλείδειο χώρο. Το σχήμα 10 δείχνει τις κορυφές, επιφάνειες και γωνίες στο τετράεδρο:

• ${\displaystyle \mathrm {S} _{k}}$ η επιφάνεια απέναντι από την κορυφή ${\displaystyle \mathrm {A} _{k}\ }$;
• ${\displaystyle s_{k}}$ η επιφάνεια του ${\displaystyle \mathrm {S} _{k}\ }$;
• ${\displaystyle \Delta _{k}}$ το επίπεδο στο οποίο το ${\displaystyle \mathrm {S} _{k}\ }$ εντάσσεται ;
• ${\displaystyle \theta _{ij}}$ η δίεδρη γωνία ${\displaystyle (\Delta _{i},\Delta _{j})}$.

Έτσι επιφάνειες και γωνίες επιβεβαιώνουν^[12] :

${\displaystyle s_{4}^{2}=s_{1}^{2}+s_{2}^{2}+s_{3}^{2}-2s_{1}s_{2}\cos \theta _{12}-2s_{1}s_{3}\cos \theta _{13}-2s_{2}s_{3}\cos \theta _{23}.\,}$

Δείτε επίσης

• Τριγωνομετρία
• Νόμος των ημιτόνων
• Νόμος των εφαπτομένων