List of Mersenne primes and perfect numbers

Mersenne primes and perfect numbers are two deeply interlinked types of natural numbers in number theory. Mersenne primes, named after the friar Marin Mersenne, are prime numbers that can be expressed as 2^p − 1 for some positive integer p. For example, 3 is a Mersenne prime as it is a prime number and is expressible as 2² − 1.^[1][2] The numbers p corresponding to Mersenne primes must themselves be prime, although not all primes p lead to Mersenne primes—for example, 2¹¹ − 1 = 2047 = 23 × 89.^[3] Meanwhile, perfect numbers are natural numbers that equal the sum of their positive proper divisors, which are divisors excluding the number itself. So, 6 is a perfect number because the proper divisors of 6 are 1, 2, and 3, and 1 + 2 + 3 = 6.^[2][4]

Visualization of 6 as a perfect number

Logarithmic graph of the number of digits of the largest known prime by year, nearly all of which have been Mersenne primes

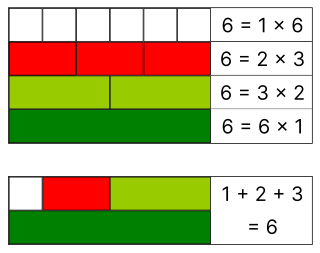
There is a one-to-one correspondence between the Mersenne primes and the even perfect numbers, but it is unknown whether there exist odd perfect numbers or not. This is due to the Euclid–Euler theorem, partially proved by Euclid and completed by Leonhard Euler: even numbers are perfect if and only if they can be expressed in the form 2^{p − 1} × (2^p − 1), where 2^p − 1 is a Mersenne prime. In other words, all numbers that fit that expression are perfect, while all even perfect numbers fit that form. For instance, in the case of p = 2, 2² − 1 = 3 is prime, and 2^{2 − 1} × (2² − 1) = 2 × 3 = 6 is perfect.^[1][5][6]

It is currently an open problem as to whether there are an infinite number of Mersenne primes and even perfect numbers.^[2][6] The frequency of Mersenne primes is the subject of the Lenstra–Pomerance–Wagstaff conjecture, which states that the expected number of Mersenne primes less than some given x is (e^γ / log 2) × log log x, where e is Euler's number, γ is Euler's constant, and log is the natural logarithm.^[7][8][9] It is also not known if any odd perfect numbers exist; various conditions on possible odd perfect numbers have been proven, including a lower bound of 10¹⁵⁰⁰.^[10]

The following is a list of all currently known Mersenne primes and perfect numbers, along with their corresponding exponents p. As of 2023^[update], there are 51 known Mersenne primes (and therefore perfect numbers), the largest 17 of which have been discovered by the distributed computing project Great Internet Mersenne Prime Search, or GIMPS.^[2] New Mersenne primes are found using the Lucas–Lehmer test (LLT), a primality test for Mersenne primes that is efficient for binary computers.^[2]

The displayed ranks are among indices currently known as of 2022^[update]; while unlikely, ranks may change if smaller ones are discovered. According to GIMPS, all possibilities less than the 48th working exponent p = 57,885,161 have been checked and verified as of January 2024^[update].^[11] The discovery year and discoverer are of the Mersenne prime, since the perfect number immediately follows by the Euclid–Euler theorem. Discoverers denoted as "GIMPS / name" refer to GIMPS discoveries with hardware used by that person. Later entries are extremely long, so only the first and last six digits of each number are shown.

Table of all 51 currently-known Mersenne primes and corresponding perfect numbers

Rank	p	Mersenne prime	Mersenne prime digits	Perfect number	Perfect number digits	Discovery	Discoverer	Method	Ref.[12]
1	2	3	1	6	1	Ancient times[lower-alpha 1]	Known to Ancient Greek mathematicians	Unrecorded	[13][14][15]
2	3	7	1	28	2				[13][14][15]
3	5	31	2	496	3				[13][14][15]
4	7	127	3	8128	4				[13][14][15]
5	13	8191	4	33550336	8	1200s/c. 1456[lower-alpha 2]	Multiple[lower-alpha 3]	Trial division	[14][15]
6	17	131071	6	8589869056	10	1588[lower-alpha 2]	Pietro Cataldi		[2][18]
7	19	524287	6	137438691328	12				[2][18]
8	31	2147483647	10	230584...952128	19	1772	Leonhard Euler	Trial division with modular restrictions	[19][20]
9	61	230584...693951	19	265845...842176	37	November 1883	Ivan Pervushin	Lucas sequences	[21]
10	89	618970...562111	27	191561...169216	54	June 1911	Ralph Ernest Powers		[22]
11	107	162259...288127	33	131640...728128	65	June 1, 1914			[23]
12	127	170141...105727	39	144740...152128	77	January 10, 1876	Édouard Lucas		[24]
13	521	686479...057151	157	235627...646976	314	January 30, 1952	Raphael M. Robinson	LLT on SWAC	[25]
14	607	531137...728127	183	141053...328128	366				[25]
15	1,279	104079...729087	386	541625...291328	770	June 25, 1952			[26]
16	2,203	147597...771007	664	108925...782528	1,327	October 7, 1952			[27]
17	2,281	446087...836351	687	994970...915776	1,373	October 9, 1952			[27]
18	3,217	259117...315071	969	335708...525056	1,937	September 8, 1957	Hans Riesel	LLT on BESK	[28]
19	4,253	190797...484991	1,281	182017...377536	2,561	November 3, 1961	Alexander Hurwitz	LLT on IBM 7090	[29]
20	4,423	285542...580607	1,332	407672...534528	2,663				[29]
21	9,689	478220...754111	2,917	114347...577216	5,834	May 11, 1963	Donald B. Gillies	LLT on ILLIAC II	[30]
22	9,941	346088...463551	2,993	598885...496576	5,985	May 16, 1963			[30]
23	11,213	281411...392191	3,376	395961...086336	6,751	June 2, 1963			[30]
24	19,937	431542...041471	6,002	931144...942656	12,003	March 4, 1971	Bryant Tuckerman	LLT on IBM 360/91	[31]
25	21,701	448679...882751	6,533	100656...605376	13,066	October 30, 1978	Landon Curt Noll & Laura Nickel	LLT on CDC Cyber 174	[32]
26	23,209	402874...264511	6,987	811537...666816	13,973	February 9, 1979	Landon Curt Noll		[32]
27	44,497	854509...228671	13,395	365093...827456	26,790	April 8, 1979	Harry L. Nelson & David Slowinski	LLT on Cray-1	[33][34]
28	86,243	536927...438207	25,962	144145...406528	51,924	September 25, 1982	David Slowinski		[35]
29	110,503	521928...515007	33,265	136204...862528	66,530	January 29, 1988	Walter Colquitt & Luke Welsh	LLT on NEC SX-2	[36][37]
30	132,049	512740...061311	39,751	131451...550016	79,502	September 19, 1983	David Slowinski et al. (Cray)	LLT on Cray X-MP	[38]
31	216,091	746093...528447	65,050	278327...880128	130,100	September 1, 1985		LLT on Cray X-MP/24	[39][40]
32	756,839	174135...677887	227,832	151616...731328	455,663	February 17, 1992		LLT on Harwell Lab's Cray-2	[41]
33	859,433	129498...142591	258,716	838488...167936	517,430	January 4, 1994		LLT on Cray C90	[42]
34	1,257,787	412245...366527	378,632	849732...704128	757,263	September 3, 1996		LLT on Cray T94	[43][44]
35	1,398,269	814717...315711	420,921	331882...375616	841,842	November 13, 1996	GIMPS / Joel Armengaud	LLT / Prime95 on 90 MHz Pentium PC	[45]
36	2,976,221	623340...201151	895,932	194276...462976	1,791,864	August 24, 1997	GIMPS / Gordon Spence	LLT / Prime95 on 100 MHz Pentium PC	[46]
37	3,021,377	127411...694271	909,526	811686...457856	1,819,050	January 27, 1998	GIMPS / Roland Clarkson	LLT / Prime95 on 200 MHz Pentium PC	[47]
38	6,972,593	437075...193791	2,098,960	955176...572736	4,197,919	June 1, 1999	GIMPS / Nayan Hajratwala	LLT / Prime95 on IBM Aptiva with 350 MHz Pentium II processor	[48]
39	13,466,917	924947...259071	4,053,946	427764...021056	8,107,892	November 14, 2001	GIMPS / Michael Cameron	LLT / Prime95 on PC with 800 MHz Athlon T-Bird processor	[49]
40	20,996,011	125976...682047	6,320,430	793508...896128	12,640,858	November 17, 2003	GIMPS / Michael Shafer	LLT / Prime95 on Dell Dimension PC with 2 GHz Pentium 4 processor	[50]
41	24,036,583	299410...969407	7,235,733	448233...950528	14,471,465	May 15, 2004	GIMPS / Josh Findley	LLT / Prime95 on PC with 2.4 GHz Pentium 4 processor	[51]
42	25,964,951	122164...077247	7,816,230	746209...088128	15,632,458	February 18, 2005	GIMPS / Martin Nowak		[52]
43	30,402,457	315416...943871	9,152,052	497437...704256	18,304,103	December 15, 2005	GIMPS / Curtis Cooper & Steven Boone	LLT / Prime95 on PC at University of Central Missouri	[53]
44	32,582,657	124575...967871	9,808,358	775946...120256	19,616,714	September 4, 2006			[54]
45	37,156,667	202254...220927	11,185,272	204534...480128	22,370,543	September 6, 2008	GIMPS / Hans-Michael Elvenich	LLT / Prime95 on PC	[55]
46	42,643,801	169873...314751	12,837,064	144285...253376	25,674,127	June 4, 2009[lower-alpha 4]	GIMPS / Odd Magnar Strindmo	LLT / Prime95 on PC with 3 GHz Intel Core 2 processor	[56]
47	43,112,609	316470...152511	12,978,189	500767...378816	25,956,377	August 23, 2008	GIMPS / Edson Smith	LLT / Prime95 on Dell OptiPlex PC with Intel Core 2 Duo E6600 processor	[55][57][58]
48	57,885,161	581887...285951	17,425,170	169296...130176	34,850,340	January 25, 2013	GIMPS / Curtis Cooper	LLT / Prime95 on PC at University of Central Missouri	[59][60]
*	69,129,889	Lowest unverified milestone[lower-alpha 5]
49[lower-alpha 6]	74,207,281	300376...436351	22,338,618	451129...315776	44,677,235	January 7, 2016[lower-alpha 7]	GIMPS / Curtis Cooper	LLT / Prime95 on PC with Intel Core i7-4790 processor	[61][62]
50[lower-alpha 6]	77,232,917	467333...179071	23,249,425	109200...301056	46,498,850	December 26, 2017	GIMPS / Jonathan Pace	LLT / Prime95 on PC with Intel Core i5-6600 processor	[63][64]
51[lower-alpha 6]	82,589,933	148894...902591	24,862,048	110847...207936	49,724,095	December 7, 2018	GIMPS / Patrick Laroche	LLT / Prime95 on PC with Intel Core i5-4590T processor	[65][66]
*	120,271,181	Lowest untested milestone[lower-alpha 5]

Historically, the largest known prime number has often been a Mersenne prime.

Notes

1. The first four perfect numbers were documented by Nicomachus circa 100, and the concept was known (along with corresponding Mersenne primes) to Euclid at the time of his Elements. There is no record of discovery.
2. Islamic mathematicians such as Ismail ibn Ibrahim ibn Fallus (1194–1239) may have known of the fifth through seventh perfect numbers prior to European records.^[16]
3. Found in an anonymous manuscript, Clm 14908, dated 1456 and 1461, and in Ibn Fallus' earlier work, which was not widely distributed^[14][17]
4. M_42,643,801 was first reported to GIMPS on April 12, 2009 but was not noticed by a human until June 4, 2009 due to a server error.
5. As of 18 September 2024^[update][11]
6. It has not been verified whether any undiscovered Mersenne primes exist between the 48th (M_57,885,161) and the 51st (M_82,589,933) on this table; the ranking is therefore provisional.
7. M_74,207,281 was first reported to GIMPS on September 17, 2015 but was not noticed by a human until January 7, 2016 due to a server error.

References

1. Stillwell, John (2010). Mathematics and Its History. Undergraduate Texts in Mathematics. Springer Science+Business Media. p. 40. ISBN 978-1-4419-6052-8. Archived from the original on 13 October 2021. Retrieved 13 October 2021.
2. Caldwell, Chris K. "Mersenne Primes: History, Theorems and Lists". PrimePages. Archived from the original on 4 October 2021. Retrieved 4 October 2021.
3. Caldwell, Chris K. "If 2ⁿ-1 is prime, then so is n". PrimePages. Archived from the original on 5 October 2021. Retrieved 12 October 2021.
4. Prielipp, Robert W. (1970). "Perfect Numbers, Abundant Numbers, and Deficient Numbers". The Mathematics Teacher. 63 (8): 692–96. doi:10.5951/MT.63.8.0692. JSTOR 27958492. Archived from the original on 5 October 2021. Retrieved 13 October 2021 – via JSTOR.
5. Caldwell, Chris K. "Characterizing all even perfect numbers". PrimePages. Archived from the original on 8 October 2014. Retrieved 12 October 2021.
6. Crilly, Tony (2007). "Perfect numbers". 50 mathematical ideas you really need to know. Quercus Publishing. ISBN 978-1-84724-008-8. Archived from the original on 13 October 2021. Retrieved 13 October 2021.
7. Caldwell, Chris K. "Heuristics Model for the Distribution of Mersennes". PrimePages. Archived from the original on 5 October 2021. Retrieved 13 October 2021.
8. Wagstaff, Samuel S. (January 1983). "Divisors of Mersenne numbers". Mathematics of Computation. 40 (161): 385–397. doi:10.1090/S0025-5718-1983-0679454-X. ISSN 0025-5718.
9. Pomerance, Carl (September 1981). "Recent developments in primality testing" (PDF). The Mathematical Intelligencer. 3 (3): 97–105. doi:10.1007/BF03022861. ISSN 0343-6993. S2CID 121750836.
10. Ochem, Pascal; Rao, Michaël (30 January 2012). "Odd perfect numbers are greater than 10¹⁵⁰⁰". Mathematics of Computation. 81 (279): 1869–1877. doi:10.1090/S0025-5718-2012-02563-4. ISSN 0025-5718.
11. "GIMPS Milestones Report". Great Internet Mersenne Prime Search. Archived from the original on 13 October 2021. Retrieved 31 January 2024.
12. Sources applying to almost all entries:

    • "List of Known Mersenne Prime Numbers". Great Internet Mersenne Prime Search. Archived from the original on 7 June 2020. Retrieved 4 October 2021.
    • Caldwell, Chris K. "Mersenne Primes: History, Theorems and Lists". PrimePages. Archived from the original on 4 October 2021. Retrieved 4 October 2021.
    • Caldwell, Chris K. "The Largest Known prime by Year: A Brief History". PrimePages. Archived from the original on 4 October 2021. Retrieved 13 October 2021.
    • Haworth, Guy M. (1987). Mersenne numbers (PDF) (Report). Archived (PDF) from the original on 13 October 2021. Retrieved 13 October 2021.
    • Noll, Landon Curt (21 December 2018). "Known Mersenne Primes". Archived from the original on 27 July 2021. Retrieved 13 October 2021.
    • Tattersall, James J. (1999). Elementary Number Theory in Nine Chapters. Cambridge University Press. pp. 131–134. ISBN 978-0-521-58531-6. Archived from the original on 13 October 2021. Retrieved 13 October 2021.
13. Joyce, David E. "Euclid's Elements, Book IX, Proposition 36". mathcs.clarku.edu. Archived from the original on 17 June 2021. Retrieved 13 October 2021.
14. Dickson, Leonard Eugene (1919). History of the Theory of Numbers, Vol. I. Carnegie Institution of Washington. pp. 4–6. Archived from the original on 2023-04-08. Retrieved 2023-03-19.
15. Smith, David Eugene (1925). History of Mathematics: Volume II. Dover. p. 21. ISBN 978-0-486-20430-7.
16. O'Connor, John J.; Robertson, Edmund F. "Perfect numbers". MacTutor History of Mathematics archive. Archived from the original on 5 October 2021. Retrieved 13 October 2021.
17. "'Calendarium ecclesiasticum – BSB Clm 14908'". Bavarian State Library. Archived from the original on 13 October 2021. Retrieved 13 October 2021.
18. Cataldi, Pietro Antonio (1603). Trattato de' numeri perfetti di Pietro Antonio Cataldo [Pietro Antonio Cataldi's treatise on perfect numbers] (in Italian). Presso di Heredi di Giouanni Rossi. Archived from the original on 2023-04-05. Retrieved 2023-03-19.
19. Caldwell, Chris K. "Modular restrictions on Mersenne divisors". PrimePages. Archived from the original on 11 November 2021. Retrieved 22 November 2021.
20. Euler, Leonhard (1772). "Extrait d'un lettre de M. Euler le pere à M. Bernoulli concernant le Mémoire imprimé parmi ceux de 1771, p 318" [Extract of a letter from Mr. Euler to Mr. Bernoulli, concerning the Mémoire published among those of 1771]. Nouveaux Mémoires de l'académie royale des sciences de Berlin (in French). 1772: 35–36. Archived from the original on 15 August 2020. Retrieved 13 October 2021 – via Euler Archive.
21. "Sur un nouveau nombre premier, annoncé par le père Pervouchine" [On a new prime number, announced by Pervouchine]. Bulletin de l'Académie impériale des sciences de St.-Pétersbourg (in French). 31: 532–533. 27 January 1887. Archived from the original on 13 October 2021. Retrieved 13 October 2021 – via Biodiversity Heritage Library.
22. Powers, R. E. (November 1911). "The Tenth Perfect Number". The American Mathematical Monthly. 18 (11): 195–197. doi:10.2307/2972574. JSTOR 2972574.
23. "Records of Proceedings at Meetings". Proceedings of the London Mathematical Society. s2-13 (1): iv–xl. 1914. doi:10.1112/plms/s2-13.1.1-s.
24. Lucas, Édouard (1876). "Note sur l'application des séries récurrentes à la recherche de la loi de distribution des nombres premiers" [Note on the application of recurrent series to researching the law of prime number distribution]. Comptes rendus de l'Académie des Sciences (in French). 82: 165–167. Archived from the original on 13 October 2021. Retrieved 13 October 2021.
25. "Notes". Mathematics of Computation. 6 (37): 58–61. January 1952. doi:10.1090/S0025-5718-52-99405-2. ISSN 0025-5718. Archived from the original on 13 October 2021. Retrieved 13 October 2021.
26. "Notes". Mathematics of Computation. 6 (39): 204–205. July 1952. doi:10.1090/S0025-5718-52-99389-7. ISSN 0025-5718.
27. "Notes". Mathematics of Computation. 7 (41): 67–72. January 1953. doi:10.1090/S0025-5718-53-99372-7. ISSN 0025-5718.
28. Riesel, Hans (January 1958). "A New Mersenne Prime". Mathematics of Computation. 12 (61): 60. doi:10.1090/S0025-5718-58-99282-2. Archived from the original on 2021-10-28. Retrieved 2021-10-13.
29. Hurwitz, Alexander (April 1962). "New Mersenne primes". Mathematics of Computation. 16 (78): 249–251. doi:10.1090/S0025-5718-1962-0146162-X. ISSN 0025-5718.
30. Gillies, Donald B. (January 1964). "Three new Mersenne primes and a statistical theory". Mathematics of Computation. 18 (85): 93–97. doi:10.1090/S0025-5718-1964-0159774-6. JSTOR 2003409.
31. Tuckerman, Bryant (October 1971). "The 24th Mersenne Prime". Proceedings of the National Academy of Sciences. 68 (10): 2319–2320. Bibcode:1971PNAS...68.2319T. doi:10.1073/pnas.68.10.2319. PMC 389411. PMID 16591945.
32. Noll, Landon Curt; Nickel, Laura (October 1980). "The 25th and 26th Mersenne primes". Mathematics of Computation. 35 (152): 1387. doi:10.1090/S0025-5718-1980-0583517-4. JSTOR 2006405.
33. Slowinski, David (1978). "Searching for the 27th Mersenne prime". Journal of Recreational Mathematics. 11 (4): 258–261.
34. "Science Watch: A New Prime Number". The New York Times. 5 June 1979. Archived from the original on 2 November 2021. Retrieved 13 October 2021.
35. "Announcements". The Mathematical Intelligencer. 5 (1): 60. March 1983. doi:10.1007/BF03023507. ISSN 0343-6993.
36. Peterson, I. (6 February 1988). "Priming for a Lucky Strike". Science News. 133 (6): 85. doi:10.2307/3972461. JSTOR 3972461.
37. Colquitt, W. N.; Welsh, L. (April 1991). "A new Mersenne prime". Mathematics of Computation. 56 (194): 867. Bibcode:1991MaCom..56..867C. doi:10.1090/S0025-5718-1991-1068823-9. JSTOR 2008415.
38. "Number is largest prime found yet". The Globe and Mail. 24 September 1983. ProQuest 386439660. Archived from the original on 2 November 2021. Retrieved 7 January 2022 – via ProQuest.
39. Peterson, I. (28 September 1985). "Prime Time for Supercomputers". Science News. 128 (13): 199. doi:10.2307/3970245. JSTOR 3970245.
40. Dembart, Lee (17 September 1985). "Supercomputer Comes Up With Whopping Prime Number". Los Angeles Times. Archived from the original on 2 November 2021. Retrieved 13 October 2021.
41. Maddox, John (26 March 1992). "The endless search for primality". Nature. 356 (6367): 283. Bibcode:1992Natur.356..283M. doi:10.1038/356283a0. ISSN 1476-4687. S2CID 4327045.
42. "Largest Known Prime Number Discovered on Cray Research Supercomputer". PR Newswire. 10 January 1994. Archived from the original on 4 November 2021. Retrieved 21 August 2023 – via Gale.
43. Caldwell, Chris K. "A Prime of Record Size! 2^1257787-1". PrimePages. Archived from the original on 5 October 2021. Retrieved 13 October 2021.
44. Gillmor, Dan (3 September 1996). "Crunching numbers: Researchers come up with prime math discovery". Knight Ridder – via Gale.
45. "GIMPS Discovers 35th Mersenne Prime, 2^1,398,269-1 is now the Largest Known Prime". Great Internet Mersenne Prime Search. 12 November 1996. Archived from the original on 7 June 2020. Retrieved 13 October 2021.
46. "GIMPS Discovers 36th Mersenne Prime, 2^2,976,221-1 is now the Largest Known Prime". Great Internet Mersenne Prime Search. 1 September 1997. Archived from the original on 7 June 2020. Retrieved 13 October 2021.
47. "GIMPS Discovers 37th Mersenne Prime, 2^3,021,377-1 is now the Largest Known Prime". Great Internet Mersenne Prime Search. 2 February 1998. Archived from the original on 7 June 2020. Retrieved 13 October 2021.
48. "GIMPS Discovers 38th Mersenne Prime 2^6,972,593-1 is now the Largest Known Prime". Great Internet Mersenne Prime Search. 30 June 1999. Archived from the original on 7 June 2020. Retrieved 13 October 2021.
49. "GIMPS Discovers 39th Mersenne Prime, 2^13,466,917-1 is now the Largest Known Prime". Great Internet Mersenne Prime Search. 6 December 2001. Archived from the original on 7 June 2020. Retrieved 13 October 2021.
50. "GIMPS Discovers 40th Mersenne Prime, 2^20,996,011-1 is now the Largest Known Prime". Great Internet Mersenne Prime Search. 2 February 2003. Archived from the original on 7 June 2020. Retrieved 13 October 2021.
51. "GIMPS Discovers 41st Mersenne Prime, 2^24,036,583-1 is now the Largest Known Prime". Great Internet Mersenne Prime Search. 28 May 2004. Archived from the original on 29 January 2021. Retrieved 13 October 2021.
52. "GIMPS Discovers 42nd Mersenne Prime, 2^25,964,951-1 is now the Largest Known Prime". Great Internet Mersenne Prime Search. 27 February 2005. Archived from the original on 14 March 2021. Retrieved 13 October 2021.
53. "GIMPS Discovers 43rd Mersenne Prime, 2^30,402,457-1 is now the Largest Known Prime". Great Internet Mersenne Prime Search. 24 December 2005. Archived from the original on 14 March 2021. Retrieved 13 October 2021.
54. "GIMPS Discovers 44th Mersenne Prime, 2^32,582,657-1 is now the Largest Known Prime". Great Internet Mersenne Prime Search. 11 September 2006. Archived from the original on 26 January 2021. Retrieved 13 October 2021.
55. "GIMPS Discovers 45th and 46th Mersenne Primes, 2^43,112,609-1 is now the Largest Known Prime". Great Internet Mersenne Prime Search. 15 September 2008. Archived from the original on 5 October 2021. Retrieved 13 October 2021.
56. "GIMPS Discovers 47th Mersenne Prime". Great Internet Mersenne Prime Search. 12 April 2009. Archived from the original on 19 February 2021. Retrieved 13 October 2021.
57. Maugh, Thomas H. (27 September 2008). "Rare prime number found". Los Angeles Times. Archived from the original on 27 July 2021. Retrieved 13 October 2021.
58. Smith, Edson. "The UCLA Mersenne Prime". UCLA Mathematics. Archived from the original on 22 November 2021. Retrieved 22 November 2021.
59. "GIMPS Discovers 48th Mersenne Prime, 2^57,885,161-1 is now the Largest Known Prime". Great Internet Mersenne Prime Search. 5 February 2013. Archived from the original on 26 January 2021. Retrieved 13 October 2021.
60. Yirka, Bob (6 February 2013). "University professor discovers largest prime number to date". phys.org. Archived from the original on 16 January 2021. Retrieved 13 October 2021.
61. "GIMPS Project Discovers Largest Known Prime Number: 2^74,207,281-1". Great Internet Mersenne Prime Search. 19 January 2016. Archived from the original on 7 January 2018. Retrieved 13 October 2021.
62. "Largest known prime number discovered in Missouri". BBC News. 20 January 2016. Archived from the original on 21 August 2021. Retrieved 13 October 2021.
63. "GIMPS Project Discovers Largest Known Prime Number: 2^77,232,917-1". Great Internet Mersenne Prime Search. 3 January 2018. Archived from the original on 4 January 2018. Retrieved 13 October 2021.
64. Lamb, Evelyn (4 January 2018). "Why You Should Care About a Prime Number That's 23,249,425 Digits Long". Slate Magazine. Archived from the original on 9 October 2021. Retrieved 13 October 2021.
65. "GIMPS Discovers Largest Known Prime Number: 2^82,589,933-1". Great Internet Mersenne Prime Search. 21 December 2018. Archived from the original on 22 December 2018. Retrieved 13 October 2021.
66. Palca, Joe (21 December 2018). "The World Has A New Largest-Known Prime Number". NPR. Archived from the original on 30 July 2021. Retrieved 13 October 2021.

External links

• OEIS sequence A000043 (Corresponding exponents p)
• OEIS sequence A000396 (Perfect numbers)
• OEIS sequence A000668 (Mersenne primes)
• List on GIMPS, with the full values of large numbers Archived 2020-06-07 at the Wayback Machine
• A technical report on the history of Mersenne numbers, by Guy Haworth Archived 2021-10-13 at the Wayback Machine