Top Qs
Timeline
Chat
Perspective
Configuration (geometry)
Points and lines with equal incidences From Wikipedia, the free encyclopedia
Remove ads
In mathematics, specifically projective geometry, a configuration in the plane consists of a finite set of points, and a finite arrangement of lines, such that each point is incident to the same number of lines and each line is incident to the same number of points.[1]

Although certain specific configurations had been studied earlier (for instance by Thomas Kirkman in 1849), the formal study of configurations was first introduced by Theodor Reye in 1876, in the second edition of his book Geometrie der Lage, in the context of a discussion of Desargues' theorem. Ernst Steinitz wrote his dissertation on the subject in 1894, and they were popularized by Hilbert and Cohn-Vossen's 1932 book Anschauliche Geometrie, reprinted in English as Hilbert & Cohn-Vossen (1952).
Configurations may be studied either as concrete sets of points and lines in a specific geometry, such as the Euclidean or projective planes (these are said to be realizable in that geometry), or as a type of abstract incidence geometry. In the latter case they are closely related to regular hypergraphs and biregular bipartite graphs, but with some additional restrictions: every two points of the incidence structure can be associated with at most one line, and every two lines can be associated with at most one point. That is, the girth of the corresponding bipartite graph (the Levi graph of the configuration) must be at least six.
Remove ads
Notation
A configuration in the plane is denoted by (pγ ℓπ), where p is the number of points, ℓ the number of lines, γ the number of lines per point, and π the number of points per line. These numbers necessarily satisfy the equation
as this product is the number of point-line incidences (flags).
Configurations having the same symbol, say (pγ ℓπ), need not be isomorphic as incidence structures. For instance, there exist three different (93 93) configurations: the Pappus configuration and two less notable configurations.
In some configurations, p = ℓ and consequently, γ = π. These are called symmetric or balanced configurations[2] and the notation is often condensed to avoid repetition. For example, (93 93) abbreviates to (93).
Remove ads
Examples
Summarize
Perspective

Notable projective configurations include the following:
- (11), the simplest possible configuration, consisting of a point incident to a line. Often excluded as being trivial.
- (32), the triangle. Each of its three sides meets two of its three vertices, and vice versa. More generally any polygon of n sides forms a configuration of type (n2)
- (43 62), the complete quadrangle
- (62 43), the Pasch configuration, which includes the complete quadrilateral
- (73), the Fano plane. This configuration exists as an abstract incidence geometry, but cannot be constructed in the Euclidean plane.
- (83), the Möbius–Kantor configuration. This configuration describes two quadrilaterals that are simultaneously inscribed and circumscribed in each other. It cannot be constructed in Euclidean plane geometry but the equations defining it have nontrivial solutions in complex numbers.
- (93), the Pappus configuration
- (94 123), the Hesse configuration of nine inflection points of a cubic curve in the complex projective plane and the twelve lines determined by pairs of these points. This configuration shares with the Fano plane the property that it contains every line through its points; configurations with this property are known as Sylvester–Gallai configurations due to the Sylvester–Gallai theorem that shows that they cannot be given real-number coordinates.[3]
- (103), the Desargues configuration
- (124 163), the Reye configuration
- (125 302), the Schläfli double six, formed by 12 of the 27 lines on a cubic surface
- (153), the Cremona–Richmond configuration, formed by the 15 lines complementary to a double six and their 15 tangent planes
- (154 203), the Cayley–Salmon configuration
- (166), the Kummer configuration
- (214), the Grünbaum–Rigby configuration
- (273), the Gray configuration
- (354), Danzer's configuration[4]
- (6015), the Klein configuration
Remove ads
Duality of configurations
The projective dual of a configuration (pγ ℓπ) is a (ℓπ pγ) configuration in which the roles of "point" and "line" are exchanged. Types of configurations therefore come in dual pairs, except when taking the dual results in an isomorphic configuration. These exceptions are called self-dual configurations and in such cases p = ℓ.[5]
The number of (n3) configurations
The number of nonisomorphic configurations of type (n3), starting at n = 7, is given by the sequence
These numbers count configurations as abstract incidence structures, regardless of realizability.[6] As Gropp (1997) discusses, nine of the ten (103) configurations, and all of the (113) and (123) configurations, are realizable in the Euclidean plane, but for each n ≥ 16 there is at least one nonrealizable (n3) configuration. Gropp also points out a long-lasting error in this sequence: an 1895 paper attempted to list all (123) configurations, and found 228 of them, but the 229th configuration, the Gropp configuration, was not discovered until 1988.
Remove ads
Constructions of symmetric configurations
Summarize
Perspective
There are several techniques for constructing configurations, generally starting from known configurations. Some of the simplest of these techniques construct symmetric (pγ) configurations.
Cyclic configurations
Some self dual configurations (pk) are cyclic configurations and can be constructed by one "generator line", like {0,1,3}, with vertices indexed from zero, and where indices in following lines are cycled forward modulo p. This is guaranteed to produce a symmetric configuration when valid. An invalid generator line produces disconnected configurations, or it may break the axiom requiring at most one line between any two points.[7]
Every polygon as configuration (p2) is trivially a cyclic configuration with generator line {0,1}. A triangle (32) has lines {{0,1},{1,2},{2,0}}.
The Fano plane, (73), the smallest self-dual order 3 symmetric configuration, can be defined by generator line {0,1,3} as lines {{0,1,3}, {1,2,4}, {2,3,5}, {3,4,6}, {4,5,0}, {5,6,1}, {6,0,2}}. They also can be represented in configuration table:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 0 |
| 3 | 4 | 5 | 6 | 0 | 1 | 2 |
The smallest self-dual order 5 symmetric configuration is (215) is a cyclic configuration and can be generated by the line {0,3,4,9,11}.[8]
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 0 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 0 | 1 | 2 |
Finite projective planes
Any finite projective plane of order n, PG(2,n), is an [(n2+n+1)n+1] configuration. Since projective planes are known to exist for all orders n which are powers of primes, these constructions provide infinite families of symmetric configurations.
Automorphisms for PG(2,n), with n=qm (q prime) are (m!)(n3-1)(n3-n)(n3-n2)/(n-1).[9]
Not all symmetric configurations are realizable. Specifically n must be a power prime. For instance, PG(2,6) or (437) configuration does not exist.[10] However, Gropp (1990) has provided a construction which shows that for k ≥ 3, a (pk) configuration exists for all p ≥ 2 ℓk + 1, where ℓk is the length of an optimal Golomb ruler of order k.
Remove ads
Unconventional configurations
Summarize
Perspective
Higher dimensions
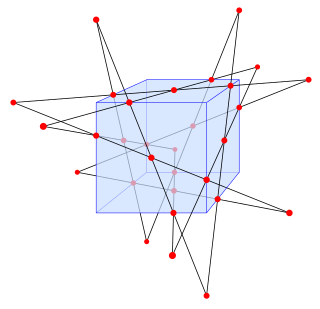
The concept of a configuration may be generalized to higher dimensions,[11] for instance to points and lines or planes in space. In such cases, the restrictions that no two points belong to more than one line may be relaxed, because it is possible for two points to belong to more than one plane.
Notable three-dimensional configurations are the Möbius configuration, consisting of two mutually inscribed tetrahedra, Reye's configuration, consisting of twelve points and twelve planes, with six points per plane and six planes per point, the Gray configuration consisting of a 3×3×3 grid of 27 points and the 27 orthogonal lines through them, and the Schläfli double six, a configuration with 30 points, 12 lines, two lines per point, and five points per line.
Topological configurations
Configuration in the projective plane that is realized by points and pseudolines is called topological configuration.[2] For instance, it is known that there exists no point-line (194) configurations, however, there exists a topological configuration with these parameters.
Configurations of points and circles
Another generalization of the concept of a configuration concerns configurations of points and circles, a notable example being the (83 64) Miquel configuration.[2]
Remove ads
See also
- Perles configuration, a set of 9 points and 9 lines which do not all have equal numbers of incidences to each other
Notes
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads

