Loading AI tools
Shortest distance between two points on the surface of a sphere From Wikipedia, the free encyclopedia
The great-circle distance, orthodromic distance, or spherical distance is the distance between two points on a sphere, measured along the great-circle arc between them. This arc is the shortest path between the two points on the surface of the sphere. (By comparison, the shortest path passing through the sphere's interior is the chord between the points.)

On a curved surface, the concept of straight lines is replaced by a more general concept of geodesics, curves which are locally straight with respect to the surface. Geodesics on the sphere are great circles, circles whose center coincides with the center of the sphere.
Any two distinct points on a sphere that are not antipodal (diametrically opposite) both lie on a unique great circle, which the points separate into two arcs; the length of the shorter arc is the great-circle distance between the points. This arc length is proportional to the central angle between the points, which if measured in radians can be scaled up by the sphere's radius to obtain the arc length. Two antipodal points both lie on infinitely many great circles, each of which they divide into two arcs of length π times the radius.
The determination of the great-circle distance is part of the more general problem of great-circle navigation, which also computes the azimuths at the end points and intermediate way-points. Because the Earth is nearly spherical, great-circle distance formulas applied to longitude and geodetic latitude of points on Earth are accurate to within about 0.5%.[1]
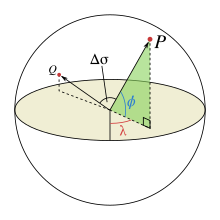
Let and be the geographical longitude and latitude of two points 1 and 2, and be their absolute differences; then , the central angle between them, is given by the spherical law of cosines if one of the poles is used as an auxiliary third point on the sphere:[2]
The problem is normally expressed in terms of finding the central angle . Given this angle in radians, the actual arc length d on a sphere of radius r can be trivially computed as
The central angle is related with the chord length of unit sphere :
For short-distance approximation (),
On computer systems with low floating point precision, the spherical law of cosines formula can have large rounding errors if the distance is small (if the two points are a kilometer apart on the surface of the Earth, the cosine of the central angle is near 0.99999999). For modern 64-bit floating-point numbers, the spherical law of cosines formula, given above, does not have serious rounding errors for distances larger than a few meters on the surface of the Earth.[3] The haversine formula is numerically better-conditioned for small distances by using the chord-length relation:[4]
Historically, the use of this formula was simplified by the availability of tables for the haversine function: and .
The following shows the equivalent formula expressing the chord length explicitly:
where .
Although this formula is accurate for most distances on a sphere, it too suffers from rounding errors for the special (and somewhat unusual) case of antipodal points. A formula that is accurate for all distances is the following special case of the Vincenty formula for an ellipsoid with equal major and minor axes:[5]
where is the two-argument arctangent. Using atan2 ensures that the correct quadrant is chosen.
Another representation of similar formulas, but using normal vectors instead of latitude and longitude to describe the positions, is found by means of 3D vector algebra, using the dot product, cross product, or a combination:[6]
where and are the normals to the sphere at the two positions 1 and 2. Similarly to the equations above based on latitude and longitude, the expression based on arctan is the only one that is well-conditioned for all angles. The expression based on arctan requires the magnitude of the cross product over the dot product.
A line through three-dimensional space between points of interest on a spherical Earth is the chord of the great circle between the points. The central angle between the two points can be determined from the chord length. The great circle distance is proportional to the central angle.
The great circle chord length, , may be calculated as follows for the corresponding unit sphere, by means of Cartesian subtraction:
Substituting and this formula can be algebraically manipulated to the form shown above in § Computational formulae.
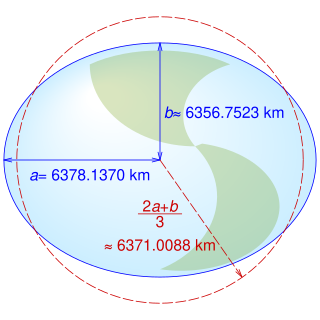
The shape of the Earth closely resembles a flattened sphere (a spheroid) with equatorial radius of 6378.137 km; distance from the center of the spheroid to each pole is 6356.7523142 km. When calculating the length of a short north-south line at the equator, the circle that best approximates that line has a radius of (which equals the meridian's semi-latus rectum), or 6335.439 km, while the spheroid at the poles is best approximated by a sphere of radius , or 6399.594 km, a 1% difference. So long as a spherical Earth is assumed, any single formula for distance on the Earth is only guaranteed correct within 0.5% (though better accuracy is possible if the formula is only intended to apply to a limited area). Using the mean Earth radius, (for the WGS84 ellipsoid) means that in the limit of small flattening, the mean square relative error in the estimates for distance is minimized.[7]
For distances smaller than 500 kilometers and outside of the poles, a Euclidean approximation of an ellipsoidal Earth (FCC's formula) is both simpler and more accurate (to 0.1%).[8]
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.