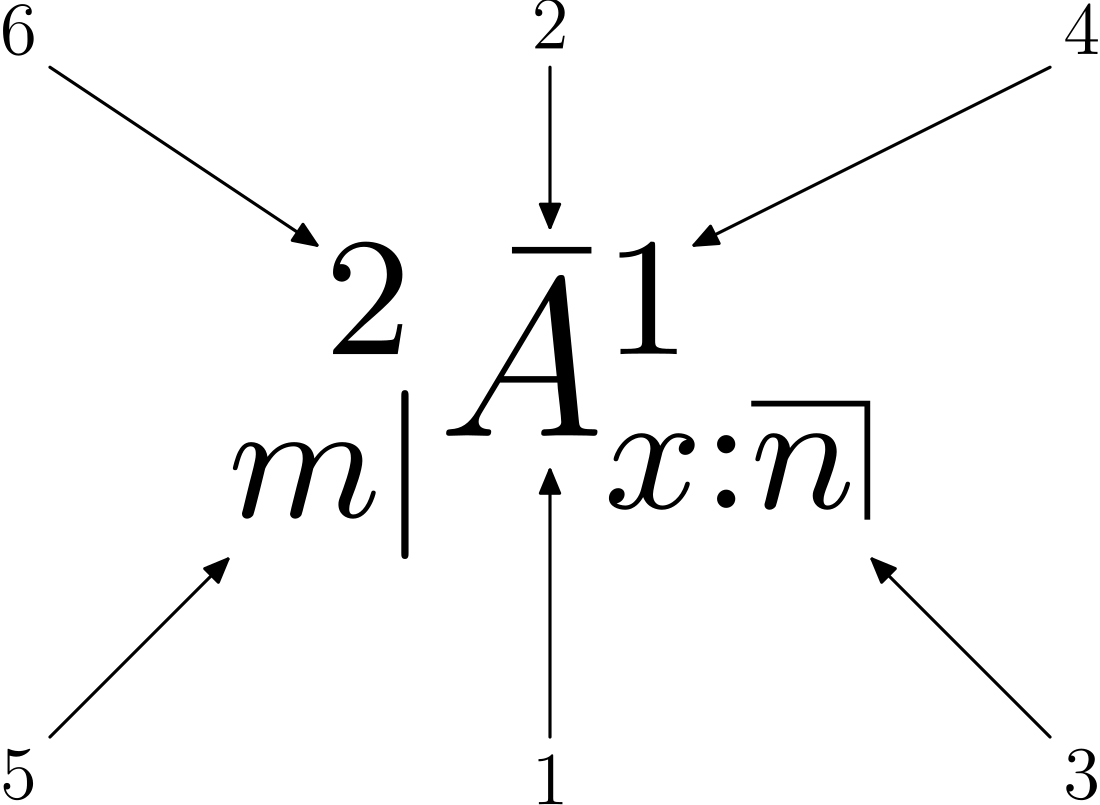Actuarial notation

Actuarial notation is a shorthand method to allow actuaries to record mathematical formulas that deal with interest rates and life tables.

Example of actuarial symbol.

1. An upper-case ${\displaystyle A}$ denotes a life assurance paying 1 on the insured event. A lower-case ${\displaystyle a}$ denotes an annuity paying 1 per annum at the appropriate time.
2. A bar indicates continuous payment or payment at the moment of death. A double dot indicates payment at the beginning of the year. No mark indicates payment at the end of the year.
3. A subscript such as ${\displaystyle x}$ denotes age, and ${\displaystyle n}$ denotes a term of ${\displaystyle n}$ years.
4. Paid if ${\displaystyle (x)}$ dies within ${\displaystyle n}$ years;
5. Deferred ${\displaystyle m}$ years.
6. No fixed meaning, implies the second moment to calculate ${\displaystyle E(Z^{2})=E{\big (}(v^{k_{x}+1})^{2}{\big )},}$ but often ${\displaystyle v^{k_{x}+1}=e^{\delta (k_{x}+1)}}$ implying double force of interest.

The core alphabet includes familiar letters such as ${\displaystyle i}$ for the effective rate of interest, ${\displaystyle v=(1+i)^{-1}}$ for the discount factor, ${\displaystyle \delta }$ for the force of interest, ${\displaystyle l_{x}}$ and ${\displaystyle q_{x}}$ for life table entries, and function letters such as ${\displaystyle a,{\ddot {a}}}$ and ${\displaystyle A}$ for annuities and insurances.^[1][2]

A distinctive feature of the system is a placement convention that uses positions around a main symbol to encode information such as the term, the ages or statuses involved, the timing of payments and the payment frequency. Typical markers include a bar over a symbol for continuous payments, a pair of dots to indicate an annuity-due and superscripts or subscripts to denote terms and ages.^[3]

An international standard form of this notation was agreed by the actuarial profession in the mid twentieth century and has remained broadly stable in modern teaching and practice.^[3][4]

Historical development and standardisation

By the first half of the twentieth century many actuarial texts used overlapping families of symbols for interest theory, life tables and life-contingent functions. To improve clarity across languages and practice areas, the profession produced an agreed statement of notation that set out a compact list of principal letters and a positional scheme for terms, ages, timing and payment frequency.^[3]

The 1949 statement described the placement zones around a symbol and gave exemplars for interest rates, discount factors, forces of interest, life table functions and life-contingent present values. It also recorded common markers, including a pair of dots above annuity symbols for payments made at the beginning of each period and a bar to indicate continuous payments.^[3]

A revision issued in 1950 consolidated this scheme and aligned professional usage in English-language syllabuses and journals. The revision reaffirmed the placement convention for terms and ages, clarified the recommended symbols for premiums and policy values and summarised the commutation function letters that remained in widespread use.^[4][1]

Example notation

Interest rates

The annual effective rate of interest is ${\displaystyle i}$. It gives the one-year growth factor ${\displaystyle 1+i}$, so an amount of 1 becomes ${\displaystyle 1+i}$ after one year and ${\displaystyle (1+i)^{n}}$ after ${\displaystyle n}$ years.^[2][1] For example, if the annual rate is 5% then ${\displaystyle i=0.05}$ and the present amount 1 grows to ${\displaystyle 1.05}$ after one year and ${\displaystyle 1.05^{3}\approx 1.1576}$ after three years.^[5]

A nominal rate of interest convertible ${\displaystyle m}$ times a year is written as ${\displaystyle i^{(m)}}$. It is paired with a periodic rate of ${\displaystyle i^{(m)}/m}$ applied ${\displaystyle m}$ times during the year, and its corresponding annual effective rate satisfies ${\displaystyle 1+i=\left(1+{\frac {i^{(m)}}{m}}\right)^{m}}$.^[2] For instance, with a nominal 12% compounded monthly, ${\displaystyle i^{(12)}=0.12}$ and ${\displaystyle 1+i=\left(1+0.12/12\right)^{12}\approx 1.1268}$, so the annual effective rate is about 12.68%.^[5]

The discount factor ${\displaystyle v}$ is the present value today of 1 payable one year from now. It equals ${\displaystyle v=(1+i)^{-1}}$.^[1] Intuitively, ${\displaystyle v}$ is the “price today” for a certain payment of 1 in one year when the market grows at rate ${\displaystyle i}$. Over multiple years, ${\displaystyle v^{n}}$ discounts a payment due in ${\displaystyle n}$ years. With ${\displaystyle i=5\%}$ we have ${\displaystyle v=1/1.05\approx 0.9524}$ and ${\displaystyle v^{3}\approx 0.8638}$.^[5]

The annual effective discount rate is ${\displaystyle d}$, defined by the relationship between amount and present value over one year. It satisfies ${\displaystyle d={\frac {i}{1+i}}}$, so ${\displaystyle 1-d=v=(1+i)^{-1}}$.^[2] Conceptually, ${\displaystyle d}$ is the fraction “taken off” one year before payment to reach the same present value as compounding at ${\displaystyle i}$ from today.

A nominal discount rate convertible ${\displaystyle m}$ times a year is written ${\displaystyle d^{(m)}}$. It is linked to the annual effective rate by ${\displaystyle 1+i=\left(1-{\frac {d^{(m)}}{m}}\right)^{-m}}$.^[1]

The force of interest ${\displaystyle \delta }$ is the limiting nominal rate under ever more frequent compounding. It gives continuous compounding via ${\displaystyle 1+i=e^{\delta }}$, so ${\displaystyle \delta =\ln(1+i)}$.^[2] With ${\displaystyle i=5\%}$ one has ${\displaystyle \delta \approx \ln(1.05)\approx 0.04879}$.

These relationships summarise the common conversions among effective, nominal and continuous descriptions of the same annual growth:

${\displaystyle (1+i)=\left(1+{\frac {i^{(m)}}{m}}\right)^{m}=e^{\delta }=\left(1-{\frac {d^{(m)}}{m}}\right)^{-m}=(1-d)^{-1}}$.^[2][1]

Life tables

A life table (or mortality table) summarises the survival pattern of a large hypothetical group, usually called a cohort. It records the number alive at each exact age and the probabilities of surviving or dying over stated intervals.^[1][2]

${\displaystyle l_{x}}$ is the number of people alive, relative to an initial cohort, at exact age ${\displaystyle x}$. As age increases the number alive falls, so ${\displaystyle l_{x+1}\leq l_{x}}$.^[1]

${\displaystyle l_{0}}$ is the starting value for ${\displaystyle l_{x}}$. It is called the radix of the table and is often a convenient round number such as ${\displaystyle 10^{5}}$ or ${\displaystyle 10^{6}}$.^[1]

${\displaystyle \omega }$ is the limiting age of the table. At and beyond this age the cohort is exhausted, so ${\displaystyle l_{n}=0}$ for all ${\displaystyle n\geq \omega }$.^[1]

${\displaystyle d_{x}}$ is the number who die between exact ages ${\displaystyle x}$ and ${\displaystyle x+1}$. It is calculated from the lives table by ${\displaystyle d_{x}=l_{x}-l_{x+1}}$.^[1]

Life table illustration

${\displaystyle x}$	${\displaystyle l_{x}}$	${\displaystyle d_{x}}$
0	${\displaystyle l_{0}}$
...	...	...
${\displaystyle x}$	${\displaystyle l_{x}}$	${\displaystyle d_{x}=l_{x}-l_{x+1}}$
${\displaystyle x+1}$	${\displaystyle l_{x+1}}$	${\displaystyle d_{x+1}}$
...	...	...
${\displaystyle \omega -1}$	${\displaystyle l_{\omega -1}}$	${\displaystyle d_{\omega -1}=l_{\omega -1}}$
${\displaystyle \omega }$	0	0

${\displaystyle q_{x}}$ is the probability that a life aged ${\displaystyle x}$ dies before reaching age ${\displaystyle x+1}$. Then

${\displaystyle q_{x}={\frac {d_{x}}{l_{x}}}}$.^[1]

${\displaystyle p_{x}}$ is the probability that a life aged ${\displaystyle x}$ survives to age ${\displaystyle x+1}$. Then

${\displaystyle p_{x}={\frac {l_{x+1}}{l_{x}}}}$.

Since surviving or dying are the only possibilities over the year,

${\displaystyle p_{x}+q_{x}=1}$.^[1]

These symbols extend naturally to multiple years by placing the number of years at the lower left. For example,

${\displaystyle {}_{n}d_{x}=l_{x}-l_{x+n}}$

is the number who die between ages ${\displaystyle x}$ and ${\displaystyle x+n}$, and the corresponding probabilities are

${\displaystyle {}_{n}q_{x}={\frac {{}_{n}d_{x}}{l_{x}}}}$ and ${\displaystyle {}_{n}p_{x}={\frac {l_{x+n}}{l_{x}}}}$.^[1]

Another statistic derived from a life table is life expectancy. The curtate expectation of life ${\displaystyle e_{x}}$ is the expected number of complete years of future life for a person aged ${\displaystyle x}$, which equals

${\displaystyle e_{x}=\sum _{t=1}^{\infty }{}_{t}p_{x}}$.^[2]

A life table usually shows ${\displaystyle l_{x}}$ at integer ages, while many actuarial models need values within the year. A common simplifying assumption is the Uniform Distribution of Deaths within each year of age, which gives linear interpolation between ${\displaystyle l_{x}}$ and ${\displaystyle l_{x+1}}$:

${\displaystyle l_{x+t}=(1-t)l_{x}+t\,l_{x+1}}$ for ${\displaystyle 0\leq t<1}$.^[1]

Annuities

Illustration of the payment streams represented by actuarial notation for annuities.

The basic symbol for the present value of an annuity is ${\displaystyle \,a}$. The following notation can then be added:

• Notation to the top-right indicates the frequency of payment (i.e., the number of annuity payments that will be made during each year). A lack of such notation means that payments are made annually.
• Notation to the bottom-right indicates the age of the person when the annuity starts and the period for which an annuity is paid.
• Notation directly above the basic symbol indicates when payments are made. Two dots indicates an annuity whose payments are made at the beginning of each year (an "annuity-due"); a horizontal line above the symbol indicates an annuity payable continuously (a "continuous annuity"); no mark above the basic symbol indicates an annuity whose payments are made at the end of each year (an "annuity-immediate").

If the payments to be made under an annuity are independent of any life event, it is known as an annuity-certain. Otherwise, in particular if payments end upon the beneficiary's death, it is called a life annuity.

${\displaystyle a_{{\overline {n|}}i}}$ (read a-angle-n at i) represents the present value of an annuity-immediate, which is a series of unit payments at the end of each year for ${\displaystyle n}$ years (in other words: the value one period before the first of n payments). This value is obtained from:

${\displaystyle \,a_{{\overline {n|}}i}=v+v^{2}+\cdots +v^{n}={\frac {1-v^{n}}{i}}}$

(${\displaystyle i}$ in the denominator matches with 'i' in immediate)

${\displaystyle {\ddot {a}}_{{\overline {n|}}i}}$ represents the present value of an annuity-due, which is a series of unit payments at the beginning of each year for ${\displaystyle n}$ years (in other words: the value at the time of the first of n payments). This value is obtained from:

${\displaystyle {\ddot {a}}_{{\overline {n|}}i}=1+v+\cdots +v^{n-1}={\frac {1-v^{n}}{d}}}$

(${\displaystyle d}$ in the denominator matches with 'd' in due)

${\displaystyle \,s_{{\overline {n|}}i}}$ is the value at the time of the last payment, ${\displaystyle {\ddot {s}}_{{\overline {n|}}i}}$ the value one period later.

If the symbol ${\displaystyle \,(m)}$ is added to the top-right corner, it represents the present value of an annuity whose payments occur each one ${\displaystyle m}$th of a year for a period of ${\displaystyle n}$ years, and each payment is one ${\displaystyle m}$th of a unit.

${\displaystyle a_{{\overline {n|}}i}^{(m)}={\frac {1-v^{n}}{i^{(m)}}}}$, ${\displaystyle {\ddot {a}}_{{\overline {n|}}i}^{(m)}={\frac {1-v^{n}}{d^{(m)}}}}$

${\displaystyle {\overline {a}}_{{\overline {n|}}i}}$ is the limiting value of ${\displaystyle \,a_{{\overline {n|}}i}^{(m)}}$ when ${\displaystyle m}$ increases without bound. The underlying annuity is known as a continuous annuity.

${\displaystyle {\overline {a}}_{{\overline {n|}}i}={\frac {1-v^{n}}{\delta }}}$

The present values of these annuities may be compared as follows:

${\displaystyle a_{{\overline {n|}}i}<a_{{\overline {n|}}i}^{(m)}<{\overline {a}}_{{\overline {n|}}i}<{\ddot {a}}_{{\overline {n|}}i}^{(m)}<{\ddot {a}}_{{\overline {n|}}i}}$

To understand the relationships shown above, consider that cash flows paid at a later time have a smaller present value than cash flows of the same total amount that are paid at earlier times.

• The subscript ${\displaystyle i}$ which represents the rate of interest may be replaced by ${\displaystyle d}$ or ${\displaystyle \delta }$, and is often omitted if the rate is clearly known from the context.
• When using these symbols, the rate of interest is not necessarily constant throughout the lifetime of the annuities. However, when the rate varies, the above formulas will no longer be valid; particular formulas can be developed for particular movements of the rate.

Life annuities

A life annuity is an annuity whose payments are contingent on the continuing life of the annuitant. The age of the annuitant is an important consideration in calculating the actuarial present value of an annuity.

• The age of the annuitant is placed at the bottom right of the symbol, without an "angle" mark.

For example:

${\displaystyle \,a_{65}}$ indicates an annuity of 1 unit per year payable at the end of each year until death to someone currently age 65

${\displaystyle a_{\overline {10|}}}$ indicates an annuity of 1 unit per year payable for 10 years with payments being made at the end of each year

${\displaystyle a_{65:{\overline {10|}}}}$ indicates an annuity of 1 unit per year for 10 years, or until death if earlier, to someone currently age 65

${\displaystyle a_{65:64}}$ indicates an annuity of 1 unit per year until the earlier death of member or death of spouse, to someone currently age 65 and spouse age 64

${\displaystyle a_{\overline {65:64}}}$ indicates an annuity of 1 unit per year until the later death of member or death of spouse, to someone currently age 65 and spouse age 64.

${\displaystyle a_{65}^{(12)}}$ indicates an annuity of 1 unit per year payable 12 times a year (1/12 unit per month) until death to someone currently age 65

${\displaystyle {\ddot {a}}_{65}}$ indicates an annuity of 1 unit per year payable at the start of each year until death to someone currently age 65

or in general:

${\displaystyle a_{x:{\overline {n|}}i}^{(m)}}$, where ${\displaystyle x}$ is the age of the annuitant, ${\displaystyle n}$ is the number of years of payments (or until death if earlier), ${\displaystyle m}$ is the number of payments per year, and ${\displaystyle i}$ is the interest rate.

In the interest of simplicity the notation is limited and does not, for example, show whether the annuity is payable to a man or a woman (a fact that would typically be determined from the context, including whether the life table is based on male or female mortality rates).

The Actuarial Present Value of life contingent payments can be treated as the mathematical expectation of a present value random variable, or calculated through the current payment form.

Life insurance

The basic symbol for a life insurance is ${\displaystyle \,A}$. The following notation can then be added:

• Notation to the top-right indicates the timing of the payment of a death benefit. A lack of notation means payments are made at the end of the year of death. A figure in parentheses (for example ${\displaystyle A^{(12)}}$) means the benefit is payable at the end of the period indicated (12 for monthly; 4 for quarterly; 2 for semi-annually; 365 for daily).
• Notation to the bottom-right indicates the age of the person when the life insurance begins.
• Notation directly above the basic symbol indicates the "type" of life insurance, whether payable at the end of the period or immediately. A horizontal line indicates life insurance payable immediately, whilst no mark above the symbol indicates payment is to be made at the end of the period indicated.

For example:

${\displaystyle \,A_{x}}$ indicates a life insurance benefit of 1 payable at the end of the year of death.

${\displaystyle \,A_{x}^{(12)}}$ indicates a life insurance benefit of 1 payable at the end of the month of death.

${\displaystyle \,{\overline {A}}_{x}}$ indicates a life insurance benefit of 1 payable at the (mathematical) instant of death.

Premium

The basic symbol for premium is ${\displaystyle \,P}$ or ${\displaystyle \,\pi }$. ${\displaystyle \,P}$ generally refers to net premiums per annum, ${\displaystyle \,\pi }$ to special premiums, as a unique premium.

Notational conventions

The table below lists principal letters that appear throughout life-contingent work and finance, with brief glosses; details and variants are given in the sections that follow.^[1][2]

Symbol	Typical meaning (plain English)
${\displaystyle i}$	effective rate of interest per period
${\displaystyle v=(1+i)^{-1}}$	discount factor per period
${\displaystyle d={\tfrac {i}{1+i}}}$	discount rate per period
${\displaystyle \delta }$	force of interest (continuous compounding)
${\displaystyle l_{x}}$, ${\displaystyle d_{x}}$	number alive at age ${\displaystyle x}$; deaths between ages ${\displaystyle x}$ and ${\displaystyle x+1}$
${\displaystyle p_{x}}$, ${\displaystyle q_{x}}$	probability of surviving one year from age ${\displaystyle x}$; probability of death within one year from age ${\displaystyle x}$
${\displaystyle a}$, ${\displaystyle {\ddot {a}}}$	present value of an annuity-immediate; present value of an annuity-due
${\displaystyle s}$, ${\displaystyle {\ddot {s}}}$	accumulated value of an annuity-immediate; accumulated value of an annuity-due
${\displaystyle A_{x}}$, ${\displaystyle {\overline {A}}_{x}}$	present value of a life insurance paying at the end of year of death; present value when payable at the moment of death
${\displaystyle P}$, ${\displaystyle V}$	net premium rate; prospective or retrospective policy value

Force of mortality

Among actuaries, force of mortality refers to what economists and other social scientists call the hazard rate and is construed as an instantaneous rate of mortality at a certain age measured on an annualized basis.

In a life table, we consider the probability of a person dying between age (x) and age x + 1; this probability is called q_x. In the continuous case, we could also consider the conditional probability that a person who has attained age (x) will die between age (x) and age (x + Δx) as:

${\displaystyle P_{\Delta x}(x)=P(x<X<x+\Delta \;x\mid \;X>x)={\frac {F_{X}(x+\Delta \;x)-F_{X}(x)}{(1-F_{X}(x))}}}$

where F_X(x) is the cumulative distribution function of the continuous age-at-death random variable, X. As Δx tends to zero, so does this probability in the continuous case. The approximate force of mortality is this probability divided by Δx. If we let Δx tend to zero, we get the function for force of mortality, denoted as μ(x):

${\displaystyle \mu \,(x)={\frac {F'_{X}(x)}{1-F_{X}(x)}}}$

See also

• Actuarial present value
• Actuarial science
• Annual percentage rate
• Mathematics of finance