Braikenridge–Maclaurin theorem

In geometry, the Braikenridge–Maclaurin theorem, named for 18th-century British mathematicians William Braikenridge and Colin Maclaurin,^[1] is the converse to Pascal's theorem. It states that if the three intersection points of the three pairs of lines through opposite sides of a hexagon lie on a line L, then the six vertices of the hexagon lie on a conic C; the conic may be degenerate, as in Pappus's hexagon theorem.^[2]

Elliptic case

Hyperbolic case

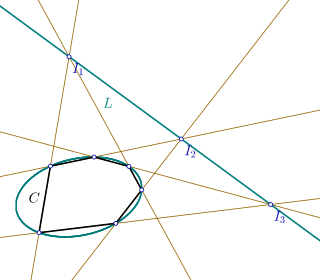
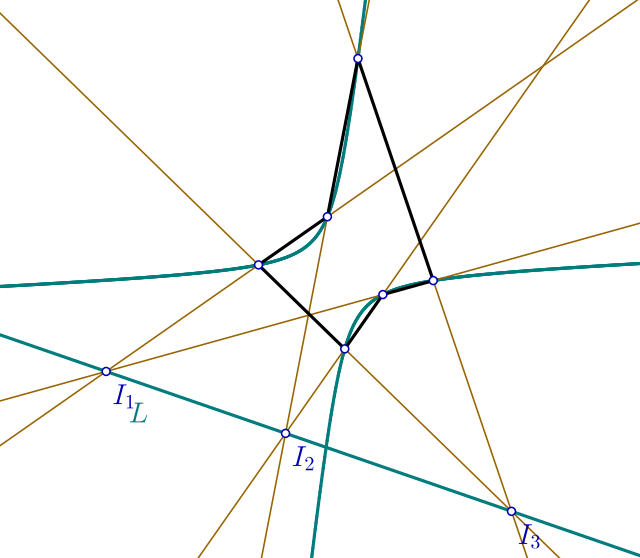
The Braikenridge–Maclaurin theorem may be applied in the Braikenridge–Maclaurin construction, which is a synthetic construction of the conic defined by five points, by varying the sixth point. Namely, Pascal's theorem states that given six points on a conic (the vertices of a hexagon), the lines defined by opposite sides intersect in three collinear points. This can be reversed to construct the possible locations for a sixth point, given five existing ones.