Zassenhaus lemma

In mathematics, the butterfly lemma or Zassenhaus lemma, named after Hans Zassenhaus, is a technical result on the lattice of subgroups of a group or the lattice of submodules of a module, or more generally for any modular lattice.^[1]

Lemma. Suppose ${\displaystyle G}$ is a group with subgroups ${\displaystyle A}$ and ${\displaystyle C}$. Suppose ${\displaystyle B\triangleleft A}$ and ${\displaystyle D\triangleleft C}$ are normal subgroups. Then there is an isomorphism of quotient groups:

${\displaystyle {\frac {(A\cap C)B}{(A\cap D)B}}\cong {\frac {(A\cap C)D}{(B\cap C)D}}.}$

Hasse diagram of the Zassenhaus "butterfly" lemma – smaller subgroups are towards the top of the diagram

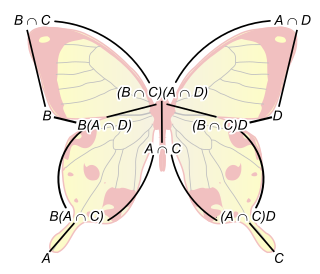
This can be generalized to the case of a group with operators ${\displaystyle (G,\Omega )}$ with stable subgroups ${\displaystyle A}$ and ${\displaystyle C}$, the above statement being the case of ${\displaystyle \Omega =G}$ acting on itself by conjugation.

Zassenhaus proved this lemma specifically to give the most direct proof of the Schreier refinement theorem. The 'butterfly' becomes apparent when trying to draw the Hasse diagram of the various groups involved.

Zassenhaus' lemma for groups can be derived from a more general result known as Goursat's theorem stated in a Goursat variety (of which groups are an instance); however the group-specific modular law also needs to be used in the derivation.^[2]