Top Qs
Timeline
Chat
Perspective
Omnitruncation
Geometric operation From Wikipedia, the free encyclopedia
Remove ads
In geometry, an omnitruncation of a convex polytope is a simple polytope of the same dimension, having a vertex for each flag of the original polytope and a facet for each face of any dimension of the original polytope. Omnitruncation is the dual operation to barycentric subdivision.[1] Because the barycentric subdivision of any polytope can be realized as another polytope,[2] the same is true for the omnitruncation of any polytope.
When omnitruncation is applied to a regular polytope (or honeycomb) it can be described geometrically as a Wythoff construction that creates a maximum number of facets. It is represented in a Coxeter–Dynkin diagram with all nodes ringed.
It is a shortcut term which has a different meaning in progressively-higher-dimensional polytopes:
- Uniform polytope truncation operators
- For regular polygons: An ordinary truncation, .
- For uniform polyhedra (3-polytopes): A cantitruncation, . (Application of both cantellation and truncation operations)
- Coxeter-Dynkin diagram:





- Coxeter-Dynkin diagram:
- For uniform polychora: A runcicantitruncation, . (Application of runcination, cantellation, and truncation operations)
- Coxeter-Dynkin diagram:






 ,
, 



 ,
, 




- Coxeter-Dynkin diagram:
- For uniform polytera (5-polytopes): A steriruncicantitruncation, t0,1,2,3,4{p,q,r,s}. . (Application of sterication, runcination, cantellation, and truncation operations)
- Coxeter-Dynkin diagram:








 ,
, 





 ,
, 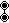




- Coxeter-Dynkin diagram:
- For uniform n-polytopes: .
Remove ads
See also
References
Further reading
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads




