Loading AI tools
2D cellular automaton devised by Edgar F. Codd in 1968 From Wikipedia, the free encyclopedia
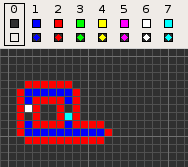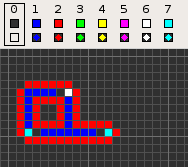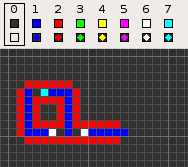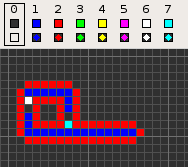
Codd's cellular automaton is a cellular automaton (CA) devised by the British computer scientist Edgar F. Codd in 1968. It was designed to recreate the computation- and construction-universality of von Neumann's CA but with fewer states: 8 instead of 29. Codd showed that it was possible to make a self-reproducing machine in his CA, in a similar way to von Neumann's universal constructor, but never gave a complete implementation.
In the 1940s and '50s, John von Neumann posed the following problem:[1]
He was able to construct a cellular automaton with 29 states, and with it a universal constructor. Codd, building on von Neumann's work, found a simpler machine with eight states.[2] This modified von Neumann's question:
Three years after Codd's work, Edwin Roger Banks showed a 4-state CA in his PhD thesis that was also capable of universal computation and construction, but again did not implement a self-reproducing machine.[3] John Devore, in his 1973 masters thesis, tweaked Codd's rules to greatly reduce the size of Codd's design. A simulation of Devore's design was demonstrated at the third Artificial Life conference in 1992, showing the final steps of construction and activation of the offspring pattern, but full self-replication was not simulated until the 2000's using Golly. Christopher Langton made another tweak to Codd's cellular automaton in 1984 to create Langton's loops, exhibiting self-replication with far fewer cells than that needed for self-reproduction in previous rules, at the cost of removing the ability for universal computation and construction.[4]
| CA | number of states | symmetries | computation- and construction-universal | size of self-reproducing machine |
|---|---|---|---|---|
| von Neumann | 29 | none | yes | 130,622 cells |
| Codd | 8 | rotations | yes | 283,126,588 cells[5] |
| Devore | 8 | rotations | yes | 94,794 cells |
| Banks IV (Banks IV Cellular Automaton) | 2 - 4 [6][3] | rotations and reflections | yes | Somewhere around 100,000,000,000 cells |
| Langton's loops | 8 | rotations | no | 86 cells |
Codd's CA has eight states determined by a von Neumann neighborhood with rotational symmetry.
The table below shows the signal-trains needed to accomplish different tasks. Some of the signal trains need to be separated by two blanks (state 1) on the wire to avoid interference, so the 'extend' signal-train used in the image at the top appears here as '70116011'.
| purpose | signal train |
|---|---|
| extend | 70116011 |
| extend_left | 4011401150116011 |
| extend_right | 5011501140116011 |
| retract | 4011501160116011 |
| retract_left | 5011601160116011 |
| retract_right | 4011601160116011 |
| mark | 701160114011501170116011 |
| erase | 601170114011501160116011 |
| sense | 70117011 |
| cap | 40116011 |
| inject_sheath | 701150116011 |
| inject_trigger | 60117011701160116011 |
Codd designed a self-replicating computer in the cellular automaton, based on Wang's W-machine. However, the design was so colossal that it evaded implementation until 2009, when Tim Hutton constructed an explicit configuration.[5] There were some minor errors in Codd's design, so Hutton's implementation differs slightly, in both the configuration and the ruleset.
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
