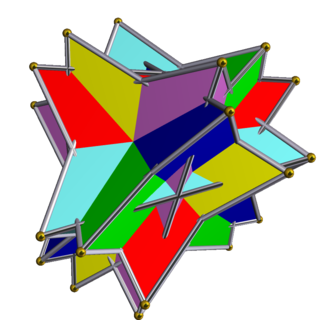
Compound of six tetrahedra with rotational freedom

The compound of six tetrahedra with rotational freedom is a uniform polyhedron compound made of a symmetric arrangement of 6 tetrahedra, considered as antiprisms. It can be constructed by superimposing six tetrahedra within a cube, and then rotating them in pairs about the three axes that pass through the centres of two opposite cubic faces. Each tetrahedron is rotated by an equal (and opposite, within a pair) angle θ. Equivalently, a tetrahedron may be inscribed within each cube in the compound of six cubes with rotational freedom, in such a way as to preserve tetrahedral symmetry.

Compound of six tetrahedra with rotational freedom
Type	Uniform compound
Index	UC1
Polyhedra	6 tetrahedra
Faces	24 triangles
Edges	36
Vertices	24
Symmetry group	tetrahedral (Td)
Subgroup restricting to one constituent	4-fold improper rotation (S4)

When θ = 0, all six tetrahedra coincide. When θ is 45 degrees, the more symmetric compound of six tetrahedra (without rotational freedom) arises.

Gallery

• Compounds of six tetrahedra with rotational freedom
• 
  File:Tetrahedron.stlθ = 0°
• 
  File:Compound_of_six_tetrahedra_with_rotational_freedom_(5°).stlθ = 5°
• 
  File:Compound_of_six_tetrahedra_with_rotational_freedom_(10°).stlθ = 10°
• 
  File:Compound_of_six_tetrahedra_with_rotational_freedom_(15°).stlθ = 15°
• 
  File:Compound_of_six_tetrahedra_with_rotational_freedom_(20°).stlθ = 20°
• 
  File:Compound_of_six_tetrahedra_with_rotational_freedom_(25°).stlθ = 25°
• 
  File:Compound_of_six_tetrahedra_with_rotational_freedom_(30°).stlθ = 30°
• 
  File:Compound_of_six_tetrahedra_with_rotational_freedom_(35°).stlθ = 35°
• 
  File:Compound_of_six_tetrahedra_with_rotational_freedom_(40°).stlθ = 40°
• 
  File:Compound_of_six_tetrahedra.stlθ = 45°

References

• Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79 (3): 447–457, doi:10.1017/S0305004100052440, MR 0397554.