Brillouin zone

In mathematics and solid state physics, the first Brillouin zone (named after Léon Brillouin) is a uniquely defined primitive cell in reciprocal space. In the same way the Bravais lattice is divided up into Wigner–Seitz cells in the real lattice, the reciprocal lattice is broken up into Brillouin zones. The boundaries of this cell are given by planes related to points on the reciprocal lattice. The importance of the Brillouin zone stems from the description of waves in a periodic medium given by Bloch's theorem, in which it is found that the solutions can be completely characterized by their behavior in a single Brillouin zone.

The reciprocal lattices (dots) and corresponding first Brillouin zones of (a) square lattice and (b) hexagonal lattice.

The first Brillouin zone is the locus of points in reciprocal space that are closer to the origin of the reciprocal lattice than they are to any other reciprocal lattice points (see the derivation of the Wigner–Seitz cell). Another definition is as the set of points in k-space that can be reached from the origin without crossing any Bragg plane. Equivalently, this is the Voronoi cell around the origin of the reciprocal lattice.

k-vectors exceeding the first Brillouin zone (red) do not carry any more information than their counterparts (black) in the first Brillouin zone. k at the Brillouin zone edge is the spatial Nyquist frequency of waves in the lattice, because it corresponds to a half-wavelength equal to the inter-atomic lattice spacing a.^[1] See also Aliasing § Sampling sinusoidal functions for more on the equivalence of k-vectors.

The Brillouin zone (purple) and the irreducible Brillouin zone (red) for a hexagonal lattice.

There are also second, third, etc., Brillouin zones, corresponding to a sequence of disjoint regions (all with the same volume) at increasing distances from the origin, but these are used less frequently. As a result, the first Brillouin zone is often called simply the Brillouin zone. In general, the n-th Brillouin zone consists of the set of points that can be reached from the origin by crossing exactly n − 1 distinct Bragg planes. A related concept is that of the irreducible Brillouin zone, which is the first Brillouin zone reduced by all of the symmetries in the point group of the lattice (point group of the crystal).

The concept of a Brillouin zone was developed by Léon Brillouin (1889–1969), a French physicist.^[2]

Within the Brillouin zone, a constant-energy surface represents the loci of all the ${\displaystyle {\vec {k}}}$-points (that is, all the electron momentum values) that have the same energy. Fermi surface is a special constant-energy surface that separates the unfilled orbitals from the filled ones at zero kelvin.

Critical points

First Brillouin zone of FCC lattice, a truncated octahedron, showing symmetry labels for high symmetry lines and points

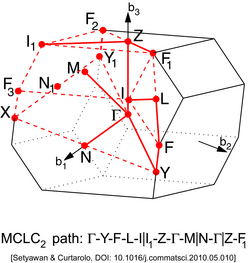
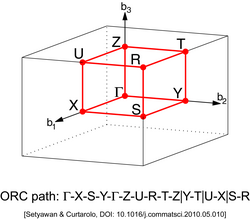
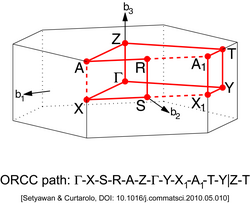
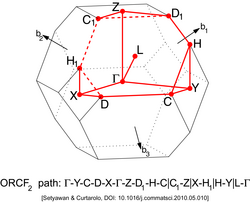
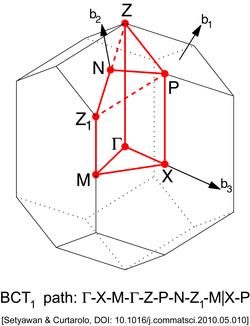
Several points of high symmetry are of special interest – these are called critical points.^[3]

Symbol	Description
Γ	Center of the Brillouin zone
Simple cube
M	Center of an edge
R	Corner point
X	Center of a face
Face-centered cubic
K	Middle of an edge joining two hexagonal faces
L	Center of a hexagonal face
U	Middle of an edge joining a hexagonal and a square face
W	Corner point
X	Center of a square face
Body-centered cubic
H	Corner point joining four edges
N	Center of a face
P	Corner point joining three edges
Hexagonal
A	Center of a hexagonal face
H	Corner point
K	Middle of an edge joining two rectangular faces
L	Middle of an edge joining a hexagonal and a rectangular face
M	Center of a rectangular face

Other lattices have different types of high-symmetry points. They can be found in the illustrations below.

Brillouin zone types^[4]

Lattice system	Bravais lattice (Abbreviation)
Triclinic	Primitive triclinic (TRI)	Triclinic Lattice type 1a (TRI1a)	Triclinic Lattice type 1b (TRI1b)	Triclinic Lattice type 2a (TRI2a)	Triclinic Lattice type 2b (TRI2b)
Monoclinic	Primitive monoclinic (MCL)	Monoclinic Lattice (MCL)
	Base-centered monoclinic (MCLC)	Base-centered monoclinic lattice type 1 (MCLC1)	Base-centered monoclinic lattice type 2 (MCLC2)	Base-centered monoclinic lattice type 3 (MCLC3)	Base-centered monoclinic lattice type 4 (MCLC4)	Base-centered monoclinic lattice type 5 (MCLC5)
Orthorhombic	Primitive orthorhombic (ORC)	Simple orthorhombic lattice (ORC)
	Base-centered orthorhombic (ORCC)	Base-centered orthorhombic lattice (ORCC)
	Body-centered orthorhombic (ORCI)	Body-centered orthorhombic lattice (ORCI)
	Face-centered orthorhombic (ORCF)	Face-centered orthorhombic lattice type 1 (ORCF1)	Face-centered orthorhombic lattice type 2 (ORCF2)	Face-centered orthorhombic lattice type 3 (ORCF3)
Tetragonal	Primitive tetragonal (TET)	Simple tetragonal lattice (TET)
	Body-centered Tetragonal (BCT)	Body-centered tetragonal lattice type 1 (BCT1)	Body-centered tetragonal lattice type 2 (BCT2)
Rhombohedral	Primitive rhombohederal (RHL)	Rhombohedral lattice type 1 (RHL1)	Rhombohedral lattice type 2 (RHL2)
Hexagonal	Primitive hexagonal (HEX)	Hexagonal lattice (HEX)
Cubic	Primitive cubic (CUB)	Simple cubic lattice (CUB)
	Body-centered cubic (BCC)	Body-centered cubic lattice (BCC)
	Face-centered cubic (FCC)	Face-centered cubic lattice (FCC)

See also

Brillouin-zone construction by selected area diffraction, using 300 keV electrons.

• Fundamental pair of periods
  • Fundamental domain