Top Qs
Timeline
Chat
Perspective
Contraposition
Mathematical logic concept From Wikipedia, the free encyclopedia
Remove ads
In logic and mathematics, contraposition, or transposition, refers to the inference of going from a conditional statement into its logically equivalent contrapositive, and an associated proof method known as § Proof by contrapositive. The contrapositive of a statement has its antecedent and consequent negated and swapped.
Conditional statement . In formulas: the contrapositive of is .[1]
If P, Then Q. — If not Q, Then not P. "If it is raining, then I wear my coat." — "If I don't wear my coat, then it isn't raining."
The law of contraposition says that a conditional statement is true if, and only if, its contrapositive is true.[2]
Contraposition () can be compared with three other operations:
- Inversion (the inverse),
- "If it is not raining, then I don't wear my coat." Unlike the contrapositive, the inverse's truth value is not at all dependent on whether or not the original proposition was true, as evidenced here.
- Conversion (the converse),
- "If I wear my coat, then it is raining." The converse is actually the contrapositive of the inverse, and so always has the same truth value as the inverse (which as stated earlier does not always share the same truth value as that of the original proposition).
- Negation (the logical complement),
- "It is not the case that if it is raining then I wear my coat.", or equivalently, "Sometimes, when it is raining, I don't wear my coat." If the negation is true, then the original proposition (and by extension the contrapositive) is false.
Note that if is true and one is given that is false (i.e., ), then it can logically be concluded that must be also false (i.e., ). This is often called the law of contrapositive, or the modus tollens rule of inference.[3]
Remove ads
Intuitive explanation
Summarize
Perspective
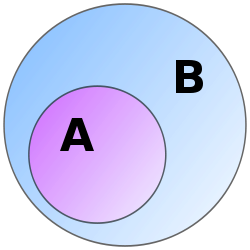
In the Euler diagram shown, if something is in A, it must be in B as well. So we can interpret "all of A is in B" as:
It is also clear that anything that is not within B (the blue region) cannot be within A, either. This statement, which can be expressed as:
is the contrapositive of the above statement. Therefore, one can say that
In practice, this equivalence can be used to make proving a statement easier. For example, if one wishes to prove that every girl in the United States (A) has brown hair (B), one can either try to directly prove by checking that all girls in the United States do indeed have brown hair, or try to prove by checking that all girls without brown hair are indeed all outside the US. In particular, if one were to find at least one girl without brown hair within the US, then one would have disproved , and equivalently .
In general, for any statement where A implies B, not B always implies not A. As a result, proving or disproving either one of these statements automatically proves or disproves the other, as they are logically equivalent to each other.
Remove ads
Formal definition
Summarize
Perspective
A proposition Q is implicated by a proposition P when the following relationship holds:
This states that, "if , then ", or, "if Socrates is a man, then Socrates is human." In a conditional such as this, is the antecedent, and is the consequent. One statement is the contrapositive of the other only when its antecedent is the negated consequent of the other, and vice versa. Thus a contrapositive generally takes the form of:
That is, "If not-, then not-", or, more clearly, "If is not the case, then P is not the case." Using our example, this is rendered as "If Socrates is not human, then Socrates is not a man." This statement is said to be contraposed to the original and is logically equivalent to it. Due to their logical equivalence, stating one effectively states the other; when one is true, the other is also true, and when one is false, the other is also false.
Strictly speaking, a contraposition can only exist in two simple conditionals. However, a contraposition may also exist in two complex, universal conditionals, if they are similar. Thus, , or "All s are s," is contraposed to , or "All non-s are non-s."[4]
Sequent notation
The transposition rule may be expressed as a sequent:
where is a metalogical symbol meaning that is a syntactic consequence of in some logical system; or as a rule of inference:
where the rule is that wherever an instance of "" appears on a line of a proof, it can be replaced with ""; or as the statement of a truth-functional tautology or theorem of propositional logic. The principle was stated as a theorem of propositional logic by Russell and Whitehead in Principia Mathematica as
where and are propositions expressed in some formal system.
Remove ads
Proofs
Summarize
Perspective
Simple proof by definition of a conditional
In first-order logic, the conditional is defined as:
which can be made equivalent to its contrapositive, as follows:
Simple proof by contradiction
Let:
It is given that, if A is true, then B is true, and it is also given that B is not true. We can then show that A must not be true by contradiction. For if A were true, then B would have to also be true (by Modus Ponens). However, it is given that B is not true, so we have a contradiction. Therefore, A is not true (assuming that we are dealing with bivalent statements that are either true or false):
We can apply the same process the other way round, starting with the assumptions that:
Here, we also know that B is either true or not true. If B is not true, then A is also not true. However, it is given that A is true, so the assumption that B is not true leads to a contradiction, which means that it is not the case that B is not true. Therefore, B must be true:
Combining the two proved statements together, we obtain the sought-after logical equivalence between a conditional and its contrapositive:
More rigorous proof of the equivalence of contrapositives
Logical equivalence between two propositions means that they are true together or false together. To prove that contrapositives are logically equivalent, we need to understand when material implication is true or false.
This is only false when is true and is false. Therefore, we can reduce this proposition to the statement "False when and not-" (i.e. "True when it is not the case that and not-"):
The elements of a conjunction can be reversed with no effect (by commutativity):
We define as equal to "", and as equal to (from this, is equal to , which is equal to just ):
This reads "It is not the case that (R is true and S is false)", which is the definition of a material conditional. We can then make this substitution:
By reverting R and S back into and , we then obtain the desired contrapositive:
In classical propositional calculus system
In Hilbert-style deductive systems for propositional logic, only one side of the transposition is taken as an axiom, and the other is a theorem. We describe a proof of this theorem in the system of three axioms proposed by Jan Łukasiewicz:
- A1.
- A2.
- A3.
(A3) already gives one of the directions of the transposition. The other side, , is proven below, using the following lemmas proven here:
- (DN1) - Double negation (one direction)
- (DN2) - Double negation (another direction)
- (HS1) - one form of Hypothetical syllogism
- (HS2) - another form of Hypothetical syllogism.
We also use the method of the hypothetical syllogism metatheorem as a shorthand for several proof steps.
The proof is as follows:
- (instance of the (DN2))
- (instance of the (HS1)
- (from (1) and (2) by modus ponens)
- (instance of the (DN1))
- (instance of the (HS2))
- (from (4) and (5) by modus ponens)
- (from (3) and (6) using the hypothetical syllogism metatheorem)
- (instance of (A3))
- (from (7) and (8) using the hypothetical syllogism metatheorem)
Remove ads
Comparisons
Summarize
Perspective
Examples
Take the statement "All red objects have color." This can be equivalently expressed as "If an object is red, then it has color."
- The contrapositive is "If an object does not have color, then it is not red." This follows logically from our initial statement and, like it, it is evidently true.
- The inverse is "If an object is not red, then it does not have color." An object which is blue is not red, and still has color. Therefore, in this case the inverse is false.
- The converse is "If an object has color, then it is red." Objects can have other colors, so the converse of our statement is false.
- The negation is "There exists a red object that does not have color." This statement is false because the initial statement which it negates is true.
In other words, the contrapositive is logically equivalent to a given conditional statement, though not sufficient for a biconditional.
Similarly, take the statement "All quadrilaterals have four sides," or equivalently expressed "If a polygon is a quadrilateral, then it has four sides."
- The contrapositive is "If a polygon does not have four sides, then it is not a quadrilateral." This follows logically, and as a rule, contrapositives share the truth value of their conditional.
- The inverse is "If a polygon is not a quadrilateral, then it does not have four sides." In this case, unlike the last example, the inverse of the statement is true.
- The converse is "If a polygon has four sides, then it is a quadrilateral." Again, in this case, unlike the last example, the converse of the statement is true.
- The negation is "There is at least one quadrilateral that does not have four sides." This statement is clearly false.
Since the statement and the converse are both true, it is called a biconditional, and can be expressed as "A polygon is a quadrilateral if, and only if, it has four sides." (The phrase if and only if is sometimes abbreviated as iff.) That is, having four sides is both necessary to be a quadrilateral, and alone sufficient to deem it a quadrilateral.
Truth
- If a statement is true, then its contrapositive is true (and vice versa).
- If a statement is false, then its contrapositive is false (and vice versa).
- If a statement's inverse is true, then its converse is true (and vice versa).
- If a statement's inverse is false, then its converse is false (and vice versa).
- If a statement's negation is false, then the statement is true (and vice versa).
- If a statement (or its contrapositive) and the inverse (or the converse) are both true or both false, then it is known as a logical biconditional.
Remove ads
Traditional logic
Summarize
Perspective
In traditional logic, contraposition is a form of immediate inference in which a proposition is inferred from another and where the former has for its subject the contradictory of the original logical proposition's predicate. In some cases, contraposition involves a change of the former's quality (i.e. affirmation or negation).[5] For its symbolic expression in modern logic, see the rule of transposition. Contraposition also has philosophical application distinct from the other traditional inference processes of conversion and obversion where equivocation varies with different proposition types.
In traditional logic, the process of contraposition is a schema composed of several steps of inference involving categorical propositions and classes.[6] A categorical proposition contains a subject and predicate where the existential impact of the copula implies the proposition as referring to a class with at least one member, in contrast to the conditional form of hypothetical or materially implicative propositions, which are compounds of other propositions, e.g. "If P, then Q" (P and Q are both propositions), and their existential impact is dependent upon further propositions where quantification existence is instantiated (existential instantiation), not on the hypothetical or materially implicative propositions themselves.
Full contraposition is the simultaneous interchange and negation of the subject and predicate, and is valid only for the type "A" and type "O" propositions of Aristotelian logic, while it is conditionally valid for "E" type propositions if a change in quantity from universal to particular is made (partial contraposition). Since the valid obverse is obtained for all the four types (A, E, I, and O types) of traditional propositions, yielding propositions with the contradictory of the original predicate, (full) contraposition is obtained by converting the obvert of the original proposition. For "E" statements, partial contraposition can be obtained by additionally making a change in quantity. Because nothing is said in the definition of contraposition with regard to the predicate of the inferred proposition, it can be either the original subject, or its contradictory, resulting in two contrapositives which are the obverts of one another in the "A", "O", and "E" type propositions.[7]
By example: from an original, 'A' type categorical proposition,
- All residents are voters,
which presupposes that all classes have members and the existential import presumed in the form of categorical propositions, one can derive first by obversion the 'E' type proposition,
- No residents are non-voters.
The contrapositive of the original proposition is then derived by conversion to another 'E' type proposition,
- No non-voters are residents.
The process is completed by further obversion resulting in the 'A' type proposition that is the obverted contrapositive of the original proposition,
- All non-voters are non-residents.
The schema of contraposition:[8]
Notice that contraposition is a valid form of immediate inference only when applied to "A" and "O" propositions. It is not valid for "I" propositions, where the obverse is an "O" proposition which has no valid converse. The contraposition of the "E" proposition is valid only with limitations (per accidens). This is because the obverse of the "E" proposition is an "A" proposition which cannot be validly converted except by limitation, that is, contraposition plus a change in the quantity of the proposition from universal to particular.
Also, notice that contraposition is a method of inference which may require the use of other rules of inference. The contrapositive is the product of the method of contraposition, with different outcomes depending upon whether the contraposition is full, or partial. The successive applications of conversion and obversion within the process of contraposition may be given by a variety of names.
The process of the logical equivalence of a statement and its contrapositive as defined in traditional class logic is not one of the axioms of propositional logic. In traditional logic there is more than one contrapositive inferred from each original statement. In regard to the "A" proposition this is circumvented in the symbolism of modern logic by the rule of transposition, or the law of contraposition. In its technical usage within the field of philosophic logic, the term "contraposition" may be limited by logicians (e.g. Irving Copi, Susan Stebbing) to traditional logic and categorical propositions. In this sense the use of the term "contraposition" is usually referred to by "transposition" when applied to hypothetical propositions or material implications.
Form of transposition
In the inferred proposition, the consequent is the contradictory of the antecedent in the original proposition, and the antecedent of the inferred proposition is the contradictory of the consequent of the original proposition. The symbol for material implication signifies the proposition as a hypothetical, or the "if–then" form, e.g. "if P, then Q".
The biconditional statement of the rule of transposition (↔) refers to the relation between hypothetical (→) propositions, with each proposition including an antecedent and consequential term. As a matter of logical inference, to transpose or convert the terms of one proposition requires the conversion of the terms of the propositions on both sides of the biconditional relationship, meaning that transposing or converting (P → Q) to (Q → P) requires that the other proposition, (¬Q → ¬P), to be transposed or converted to (¬P → ¬Q). Otherwise, converting the terms of one proposition and not the other renders the rule invalid, violating the sufficient condition and necessary condition of the terms of the propositions, where the violation is that the changed proposition commits the fallacy of denying the antecedent or affirming the consequent by means of illicit conversion.
The truth of the rule of transposition is dependent upon the relations of sufficient condition and necessary condition in logic.
Sufficient condition
In the proposition "If P, then Q", the occurrence of P is sufficient reason for the occurrence of Q. P, as an individual or a class, materially implicates Q, but the relation of Q to P is such that the converse proposition "If Q, then P" does not necessarily have sufficient condition. The rule of inference for sufficient condition is modus ponens, which is an argument for conditional implication:
- Premise (1): If P, then Q
- Premise (2): P
- Conclusion: Therefore, Q
Necessary condition
Since the converse of premise (1) is not valid, all that can be stated of the relationship of P and Q is that in the absence of Q, P does not occur, meaning that Q is the necessary condition for P. The rule of inference for necessary condition is modus tollens:
- Premise (1): If P, then Q
- Premise (2): not Q
- Conclusion: Therefore, not P
Necessity and sufficiency example
An example traditionally used by logicians contrasting sufficient and necessary conditions is the statement "If there is fire, then oxygen is present". An oxygenated environment is necessary for fire or combustion, but simply because there is an oxygenated environment does not necessarily mean that fire or combustion is occurring. While one can infer that fire stipulates the presence of oxygen, from the presence of oxygen the converse "If there is oxygen present, then fire is present" cannot be inferred. All that can be inferred from the original proposition is that "If oxygen is not present, then there cannot be fire".
Relationship of propositions
The symbol for the biconditional ("↔") signifies the relationship between the propositions is both necessary and sufficient, and is verbalized as "if and only if", or, according to the example "If P, then Q 'if and only if' if not Q, then not P".
Necessary and sufficient conditions can be explained by analogy in terms of the concepts and the rules of immediate inference of traditional logic. In the categorical proposition "All S is P", the subject term S is said to be distributed, that is, all members of its class are exhausted in its expression. Conversely, the predicate term P cannot be said to be distributed, or exhausted in its expression because it is indeterminate whether every instance of a member of P as a class is also a member of S as a class. All that can be validly inferred is that "Some P are S". Thus, the type "A" proposition "All P is S" cannot be inferred by conversion from the original type "A" proposition "All S is P". All that can be inferred is the type "A" proposition "All non-P is non-S" (note that (P → Q) and (¬Q → ¬P) are both type "A" propositions). Grammatically, one cannot infer "all mortals are men" from "All men are mortal". An type "A" proposition can only be immediately inferred by conversion when both the subject and predicate are distributed, as in the inference "All bachelors are unmarried men" from "All unmarried men are bachelors".
Remove ads
Distinguished from transposition
Summarize
Perspective
While most authors use the terms for the same thing, some authors distinguish transposition from contraposition. In traditional logic the reasoning process of transposition as a rule of inference is applied to categorical propositions through contraposition and obversion,[9] a series of immediate inferences where the rule of obversion is first applied to the original categorical proposition "All S is P"; yielding the obverse "No S is non-P". In the obversion of the original proposition to a type "E" proposition, both terms become distributed. The obverse is then converted, resulting in "No non-P is S", maintaining distribution of both terms. The "No non-P is S" is again obverted, resulting in the [contrapositive] "All non-P is non-S". Since nothing is said in the definition of contraposition with regard to the predicate of the inferred proposition, it is permissible that it could be the original subject or its contradictory, and the predicate term of the resulting type "A" proposition is again undistributed. This results in two contrapositives, one where the predicate term is distributed, and another where the predicate term is undistributed.[10]
Contraposition is a type of immediate inference in which from a given categorical proposition another categorical proposition is inferred which has as its subject the contradictory of the original predicate. Since nothing is said in the definition of contraposition with regard to the predicate of the inferred proposition, it is permissible that it could be the original subject or its contradictory. This is in contradistinction to the form of the propositions of transposition, which may be material implication, or a hypothetical statement. The difference is that in its application to categorical propositions the result of contraposition is two contrapositives, each being the obvert of the other,[11] i.e. "No non-P is S" and "All non-P is non-S". The distinction between the two contrapositives is absorbed and eliminated in the principle of transposition, which presupposes the "mediate inferences"[12] of contraposition and is also referred to as the "law of contraposition".[13]
Remove ads
Proof by contrapositive
Summarize
Perspective
Because the contrapositive of a statement always has the same truth value (truth or falsity) as the statement itself, it can be a powerful tool for proving mathematical theorems (especially if the truth of the contrapositive is easier to establish than the truth of the statement itself). A proof by contrapositive is a direct proof of the contrapositive of a statement.[14] However, indirect methods such as proof by contradiction can also be used with contraposition, as, for example, in the proof of the irrationality of the square root of 2. By the definition of a rational number, the statement can be made that "If is rational, then it can be expressed as an irreducible fraction". This statement is true because it is a restatement of a definition. The contrapositive of this statement is "If cannot be expressed as an irreducible fraction, then it is not rational". This contrapositive, like the original statement, is also true. Therefore, if it can be proven that cannot be expressed as an irreducible fraction, then it must be the case that is not a rational number. The latter can be proved by contradiction.
The previous example employed the contrapositive of a definition to prove a theorem. One can also prove a theorem by proving the contrapositive of the theorem's statement. To prove that if a positive integer N is a non-square number, its square root is irrational, we can equivalently prove its contrapositive, that if a positive integer N has a square root that is rational, then N is a square number. This can be shown by setting √N equal to the rational expression a/b with a and b being positive integers with no common prime factor, and squaring to obtain N = a2/b2 and noting that since N is a positive integer b=1 so that N = a2, a square number.
In mathematics, proof by contrapositive, or proof by contraposition, is a rule of inference used in proofs, where one infers a conditional statement from its contrapositive.[15] In other words, the conclusion "if A, then B" is inferred by constructing a proof of the claim "if not B, then not A" instead. More often than not, this approach is preferred if the contrapositive is easier to prove than the original conditional statement itself.
Logically, the validity of proof by contrapositive can be demonstrated by the use of the following truth table, where it is shown that p → q and q → p share the same truth values in all scenarios:
Difference with proof by contradiction
Proof by contradiction: Assume (for contradiction) that is true. Use this assumption to prove a contradiction. It follows that is false, so is true.
Proof by contrapositive: To prove , prove its contrapositive statement, which is .
Example
Let be an integer.
- To prove: If is even, then is even.
Although a direct proof can be given, we choose to prove this statement by contraposition. The contrapositive of the above statement is:
- If is not even, then is not even.
This latter statement can be proven as follows: suppose that x is not even, then x is odd. The product of two odd numbers is odd, hence is odd. Thus is not even.
Having proved the contrapositive, we can then infer that the original statement is true.[16]
Remove ads
In nonclassical logics
Summarize
Perspective
Intuitionistic logic
In intuitionistic logic, the statement cannot be proven to be equivalent to . We can prove that implies (see below) without additional assumptions, but the reverse implication, from to , requires knowing , which follows from the law of the excluded middle or an equivalent axiom.
Assume (initial assumption)
- Assume
- From and , conclude
- Discharge assumption; conclude
- Turning into , conclude
Discharge assumption; conclude .
Subjective logic
Contraposition represents an instance of the subjective Bayes' theorem in subjective logic expressed as:
where denotes a pair of binomial conditional opinions given by source . The parameter denotes the base rate (aka. the prior probability) of . The pair of derivative inverted conditional opinions is denoted . The conditional opinion generalizes the logical statement , i.e. in addition to assigning TRUE or FALSE the source can assign any subjective opinion to the statement. The case where is an absolute TRUE opinion is equivalent to source saying that is TRUE, and the case where is an absolute FALSE opinion is equivalent to source saying that is FALSE. In the case when the conditional opinion is absolute TRUE the subjective Bayes' theorem operator of subjective logic produces an absolute FALSE derivative conditional opinion and thereby an absolute TRUE derivative conditional opinion which is equivalent to being TRUE. Hence, the subjective Bayes' theorem represents a generalization of both contraposition and Bayes' theorem.[17]
Remove ads
In probability theory
Summarize
Perspective
Contraposition represents an instance of Bayes' theorem which in a specific form can be expressed as:
In the equation above the conditional probability generalizes the logical statement , i.e. in addition to assigning TRUE or FALSE we can also assign any probability to the statement. The term denotes the base rate (aka. the prior probability) of . Assume that is equivalent to being TRUE, and that is equivalent to being FALSE. It is then easy to see that when i.e. when is TRUE. This is because so that the fraction on the right-hand side of the equation above is equal to 1, and hence which is equivalent to being TRUE. Hence, Bayes' theorem represents a generalization of contraposition.[18]
Remove ads
See also
References
Sources
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads






















































































