Natural number

In mathematics, the natural numbers are the numbers 0, 1, 2, 3, and so on, possibly excluding 0.^[a][1] The terms positive integers, non-negative integers, whole numbers, and counting numbers are also used.^[2][3] The set of the natural numbers is commonly denoted with a bold N or a blackboard bold ⁠${\displaystyle \mathbb {N} }$⁠.

Natural numbers can be used for counting: one apple; two apples are one apple added to another apple, three apples are one apple added to two apples, ...

The natural numbers are used for counting, and for labeling the result of a count, like "there are seven days in a week", in which case they are called cardinal numbers. They are also used to label places in an ordered series, like "the third day of the month", in which case they are called ordinal numbers. Natural numbers may also be used to label, like the jersey numbers of a sports team; in this case, they have no specific mathematical properties and are called nominal numbers.^[4]

Two natural operations are defined on natural numbers, addition and multiplication. Arithmetic is the study of the ways to perform these operations. Number theory is the study of the properties of these operations and their generalizations. Much of combinatorics involves counting mathematical objects, patterns and structures that are defined using natural numbers.

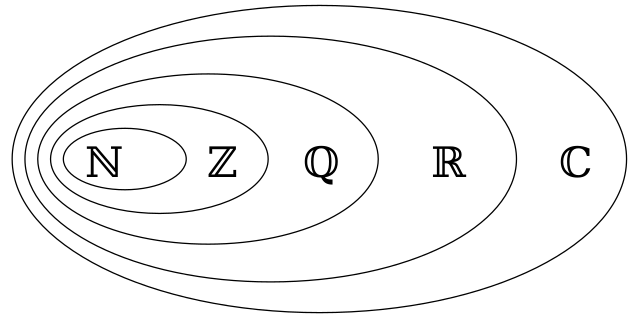
Many number systems are built from the natural numbers and contain them. For example, the integers are made by including 0 and negative numbers. The rational numbers add fractions, and the real numbers add all infinite decimals. Complex numbers add the square root of −1.^[5] This makes up natural numbers as foundational for all mathematics.^[6]

Terminology and notation

The term natural numbers has two common definitions: either 0, 1, 2, ... or 1, 2, 3, .... Because there is no universal convention, the definition can be chosen to suit the context of use.^[1][7] To eliminate ambiguity, the sequences 1, 2, 3, ... and 0, 1, 2, ... are often called the positive integers and the non-negative integers, respectively.

The phrase whole numbers is frequently used for the natural numbers that include 0, although it may also mean all integers, positive and negative.^[8][2] In primary education, counting numbers usually refer to the natural numbers starting at 1,^[3] though this definition can vary.^[9][10]

The set of all natural numbers is typically denoted N or in blackboard bold as ${\displaystyle \mathbb {N} .}$^[7][11][b] Whether 0 is included is often determined by the context but may also be specified by using ${\displaystyle \mathbb {N} }$ or ${\displaystyle \mathbb {Z} }$ (the set of all integers) with a subscript or superscript. Examples include ${\displaystyle \mathbb {N} _{1}}$,^[13] or ${\displaystyle \mathbb {Z} ^{+}}$^[14] (for the set starting at 1) and ${\displaystyle \mathbb {N} _{0}}$^[15] or ${\displaystyle \mathbb {Z} ^{0+}}$^[16] (for the set including 0).

Intuitive concept

An intuitive and implicit understanding of natural numbers is developed naturally through using numbers for counting, ordering and basic arithmetic. Within this are two closely related aspects of what a natural number is: the size of a collection; and a position in a sequence.

Size of a collection

Natural numbers can be used to answer questions like: "how many apples are on the table?".^[17] A natural number used in this way describes a characteristic of a collection of objects. This characteristic, the size of a collection is called cardinality and a natural number used to describe or measure it is called a cardinal number.

A group of apples and group of oranges with the same cardinality.

Two collections have the same size or cardinality if there is a one-to-one correspondence between the objects in each collection to the objects in the other. For example, in the image to the right every apple can be paired off with one orange and every orange can be paired off with one apple. From this, even without counting or using numbers it can be seen that the group of apples has the same cardinality as the group of oranges, meaning they are both assigned the same cardinal number.

The natural number 3 is the thing used for the particular cardinal number described above and for the cardinal number of any other collection of objects that could be paired off in the same way to one of these groups.

Position in a sequence

The natural numbers have a fixed progression, which is the familiar sequence beginning with 1, 2, 3, and so on. A natural number can be used to denote a specific position in any other sequence, in which case it is called an ordinal number. To have a specific position in a sequence means to come either before or after every other position in the sequence in a defined way, which is the concept of order.

The natural number 3 then is the thing that comes after 2 and 1, and before 4, 5 and so on. The number 2 is the thing that comes after 1, and 1 is the first element in the sequence. Each number represents the relation that position bears to the rest of the infinite sequence.^[18]

Counting

The process of counting involves both the cardinal and ordinal use of the natural numbers and illustrates the way the two fit together. To count the number of objects in a collection, each object is paired off with a natural number, usually by mentally or verbally saying the name of the number and assigning it to a particular object. The numbers must be assigned in order starting with 1 (they are ordinal) but the order of the objects chosen is arbitrary as long as each object is assigned one and only one number. When all of the objects have been assigned a number, the ordinal number assigned to the final object gives the result of the count, which is the cardinal number of the whole collection.

History

Ancient roots

Further information: Prehistoric counting

The Ishango bone (on exhibition at the Royal Belgian Institute of Natural Sciences)^[19][20][21] is believed to have been used 20,000 years ago for natural number arithmetic.

The most primitive method of representing a natural number is to use one's fingers, as in finger counting. Putting down a tally mark for each object is another primitive method. Later, a set of objects could be tested for equality, excess or shortage—by striking out a mark and removing an object from the set.

The first major advance in abstraction was the use of numerals to represent numbers. This allowed systems to be developed for recording large numbers. The ancient Egyptians developed a powerful system of numerals with distinct hieroglyphs for 1, 10, and all powers of 10 up to over 1 million. A stone carving from Karnak, dating back from around 1500 BCE and now at the Louvre in Paris, depicts 276 as 2 hundreds, 7 tens, and 6 ones; and similarly for the number 4,622. The Babylonians had a place-value system based essentially on the numerals for 1 and 10, using base sixty, so that the symbol for sixty was the same as the symbol for one—its value being determined from context.^[22]

A much later advance was the development of the idea that 0 can be considered as a number, with its own numeral. The use of a 0 digit in place-value notation (within other numbers) dates back as early as 700 BCE by the Babylonians, who omitted such a digit when it would have been the last symbol in the number.^[c] The Olmec and Maya civilizations used 0 as a separate number as early as the 1st century BCE, but this usage did not spread beyond Mesoamerica.^[24][25] The use of a numeral 0 in modern times originated with the Indian mathematician Brahmagupta in 628 CE. However, 0 had been used as a number in the medieval computus (the calculation of the date of Easter), beginning with Dionysius Exiguus in 525 CE, without being denoted by a numeral. Standard Roman numerals do not have a symbol for 0; instead, nulla (or the genitive form nullae) from nullus, the Latin word for "none", was employed to denote a 0 value.^[26]

The first systematic study of numbers as abstractions is usually credited to the Greek philosophers Pythagoras and Archimedes. Some Greek mathematicians treated the number 1 differently than larger numbers, sometimes even not as a number at all.^[d] Euclid, for example, defined a unit first and then a number as a multitude of units, thus by his definition, a unit is not a number and there are no unique numbers (e.g., any two units from indefinitely many units is a 2).^[28] However, in the definition of perfect number which comes shortly afterward, Euclid treats 1 as a number like any other.^[29]

Independent studies on numbers also occurred at around the same time in India, China, and Mesoamerica.^[30]

Emergence as a term

Nicolas Chuquet used the term progression naturelle (natural progression) in 1484.^[31] The earliest known use of "natural number" as a complete English phrase is in 1763.^[32][33] The 1771 Encyclopaedia Britannica defines natural numbers in the logarithm article.^[33]

Starting at 0 or 1 has long been a matter of definition. In 1727, Bernard Le Bovier de Fontenelle wrote that his notions of distance and element led to defining the natural numbers as including or excluding 0.^[34] In 1889, Giuseppe Peano used N for the positive integers and started at 1,^[35] but he later changed to using N₀ and N₁.^[36] Historically, most definitions have excluded 0,^[33][37][38] but many mathematicians such as George A. Wentworth, Bertrand Russell, Nicolas Bourbaki, Paul Halmos, Stephen Cole Kleene, and John Horton Conway have preferred to include 0.^[39][33] This approach gained wider adoption in the 1960s^[33] and was formalized in ISO 31-11 (1978), which defines natural numbers to include zero, a convention retained in the current ISO 80000-2 standard.^[40]

Formal construction

In 19th century Europe, there was mathematical and philosophical discussion about the exact nature of the natural numbers. Henri Poincaré stated that axioms can only be demonstrated in their finite application, and concluded that it is "the power of the mind" which allows conceiving of the indefinite repetition of the same act.^[41] Leopold Kronecker summarized his belief as "God made the integers, all else is the work of man".^[e]

The constructivists saw a need to improve upon the logical rigor in the foundations of mathematics.^[f] In the 1860s, Hermann Grassmann suggested a recursive definition for natural numbers, thus stating they were not really natural—but a consequence of definitions. Later, two classes of such formal definitions emerged, using set theory and Peano's axioms respectively. Later still, they were shown to be equivalent in most practical applications.

Set-theoretical definitions of natural numbers were initiated by Frege. He initially defined a natural number as the class of all sets that are in one-to-one correspondence with a particular set. However, this definition turned out to lead to paradoxes, including Russell's paradox. To avoid such paradoxes, the formalism was modified so that a natural number is defined as a particular set, and any set that can be put into one-to-one correspondence with that set is said to have that number of elements.^[44]

In 1881, Charles Sanders Peirce provided the first axiomatization of natural-number arithmetic.^[45][46] In 1888, Richard Dedekind proposed another axiomatization of natural-number arithmetic,^[47] and in 1889, Peano published a simplified version of Dedekind's axioms in his book The principles of arithmetic presented by a new method (Latin: Arithmetices principia, nova methodo exposita). This approach is now called Peano arithmetic. It is based on an axiomatization of the properties of ordinal numbers: each natural number has a successor and every non-zero natural number has a unique predecessor. Peano arithmetic is equiconsistent with several weak systems of set theory. One such system is ZFC with the axiom of infinity replaced by its negation.^[48] Theorems that can be proved in ZFC but cannot be proved using the Peano Axioms include Goodstein's theorem.^[49]

Formal definitions

Formal definitions of the natural numbers take the existing, intuitive notion of natural numbers and the rules of arithmetic and define them both in the more fundamental terms of mathematical logic. The two standard methods for doing this are: the Peano axioms; and set theory.

The Peano axioms (named for Giuseppe Peano) do not explicitly define what the natural numbers are, but instead comprise a list of statements or axioms that must be true of natural numbers, however they are defined. In contrast, set theory defines each natural number as a particular set, in which a set can be generally understood as a collection of distinct objects or elements. While the two approaches are different, they are consistent in that the natural number sets collectively satisfy the Peano axioms.

Peano axioms

Main article: Peano axioms

The five Peano axioms are the following:^[50][g]

1. 0 is a natural number.
2. Every natural number has a successor which is also a natural number.
3. 0 is not the successor of any natural number.
4. If the successor of ${\displaystyle x}$ equals the successor of ${\displaystyle y}$, then ${\displaystyle x}$ equals ${\displaystyle y}$.
5. The axiom of induction: If a statement is true of 0, and if the truth of that statement for a number implies its truth for the successor of that number, then the statement is true for every natural number.

These are not the original axioms published by Peano, but are named in his honor. Some forms of the Peano axioms have 1 in place of 0. In ordinary arithmetic, the successor of ${\displaystyle x}$ is ${\displaystyle x+1}$.

Set-theoretic definition

Main articles: Set-theoretic definition of natural numbers and von Neumann ordinal

In set theory each natural number n is defined as an explicitly defined set, whose elements allow counting the elements of other sets. A variety of different constructions have been proposed, however the standard solution (due to John von Neumann)^[51] is to define each natural number n as a set containing n elements in the following way:

• Call 0 = { }, the empty set.
• Define the successor S(a) of any set a by S(a) = a ∪ {a}.
• By the axiom of infinity, there exist sets which contain 0 and are closed under the successor function. Such sets are said to be inductive. The intersection of all inductive sets is still an inductive set.
• This intersection is the set of the natural numbers.

This produces an iterative definition of the natural numbers satisfying the Peano axioms, sometimes called von Neumann ordinals:

• 0 = { }
• 1 = 0 ∪ {0} = {0} = {{ }}
• 2 = 1 ∪ {1} = {0, 1} = {{ }, {{ }}}
• 3 = 2 ∪ {2} = {0, 1, 2} = {{ }, {{ }}, {{ }, {{ }}}}
• n = n−1 ∪ {n−1} = {0, 1, ..., n−1} = {{ }, {{ }}, ..., {{ }, {{ }}, ...}}

In this definition each natural number is equal to the set of all natural numbers less than it. Given a natural number n, the sentence "a set S has n elements" can be formally defined as "there exists a bijection from n to S." This formalizes the operation of counting the elements of S. Also, n ≤ m if and only if n is a subset of m. In other words, the set inclusion defines the usual total order on the natural numbers. This order is a well-order.

Another construction sometimes called Zermelo ordinals^[52] defines 0 = { } and S(a) = {a} and is now largely only of historical interest.

Properties

This section uses the convention ${\displaystyle \mathbb {N} =\mathbb {N} _{0}=\mathbb {N} ^{*}\cup \{0\}}$.

Addition

Given the set ${\displaystyle \mathbb {N} }$ of natural numbers and the successor function ${\displaystyle S\colon \mathbb {N} \to \mathbb {N} }$ sending each natural number to the next one, one can define addition of natural numbers recursively by setting a + 0 = a and a + S(b) = S(a + b) for all a, b. Thus, a + 1 = a + S(0) = S(a+0) = S(a), a + 2 = a + S(1) = S(a+1) = S(S(a)), and so on. The algebraic structure ${\displaystyle (\mathbb {N} ,+)}$ is a commutative monoid with identity element 0. It is a free monoid on one generator. This commutative monoid satisfies the cancellation property, so it can be embedded in a group. The smallest group containing the natural numbers is the integers.

If 1 is defined as S(0), then b + 1 = b + S(0) = S(b + 0) = S(b). That is, b + 1 is simply the successor of b.

Multiplication

Analogously, given that addition has been defined, a multiplication operator ${\displaystyle \times }$ can be defined via a × 0 = 0 and a × S(b) = (a × b) + a. This turns ${\displaystyle (\mathbb {N} ^{*},\times )}$ into a free commutative monoid with identity element 1; a generator set for this monoid is the set of prime numbers.

Relationship between addition and multiplication

Addition and multiplication are compatible, which is expressed in the distribution law: a × (b + c) = (a × b) + (a × c). These properties of addition and multiplication make the natural numbers an instance of a commutative semiring. Semirings are an algebraic generalization of the natural numbers where multiplication is not necessarily commutative. The lack of additive inverses, which is equivalent to the fact that ${\displaystyle \mathbb {N} }$ is not closed under subtraction (that is, subtracting one natural from another does not always result in another natural), means that ${\displaystyle \mathbb {N} }$ is not a ring; instead it is a semiring (also known as a rig).

If the natural numbers are taken as "excluding 0", and "starting at 1", the definitions of + and × are as above, except that they begin with a + 1 = S(a) and a × 1 = a. Furthermore, ${\displaystyle (\mathbb {N^{*}} ,+)}$ has no identity element.

Order

In this section, juxtaposed variables such as ab indicate the product a × b,^[53] and the standard order of operations is assumed.

A total order on the natural numbers is defined by letting a ≤ b if and only if there exists another natural number c where a + c = b. This order is compatible with the arithmetical operations in the following sense: if a, b and c are natural numbers and a ≤ b, then a + c ≤ b + c and ac ≤ bc.

An important property of the natural numbers is that they are well-ordered: every non-empty set of natural numbers has a least element. The rank among well-ordered sets is expressed by an ordinal number; for the natural numbers, this is denoted as ω (omega).

Division

In this section, juxtaposed variables such as ab indicate the product a × b, and the standard order of operations is assumed.

While it is in general not possible to divide one natural number by another and get a natural number as result, the procedure of division with remainder or Euclidean division is available as a substitute: for any two natural numbers a and b with b ≠ 0 there are natural numbers q and r such that

${\displaystyle a=bq+r{\text{ and }}r<b.}$

The number q is called the quotient and r is called the remainder of the division of a by b. The numbers q and r are uniquely determined by a and b. This Euclidean division is key to the several other properties (divisibility), algorithms (such as the Euclidean algorithm), and ideas in number theory.

Algebraic properties satisfied by the natural numbers

The addition (+) and multiplication (×) operations on natural numbers as defined above have several algebraic properties:

• Closure under addition and multiplication: for all natural numbers a and b, both a + b and a × b are natural numbers.^[54]
• Associativity: for all natural numbers a, b, and c, a + (b + c) = (a + b) + c and a × (b × c) = (a × b) × c.^[55]
• Commutativity: for all natural numbers a and b, a + b = b + a and a × b = b × a.^[56]
• Existence of identity elements: for every natural number a, a + 0 = a and a × 1 = a.
  • If the natural numbers are taken as "excluding 0", and "starting at 1", then for every natural number a, a × 1 = a. However, the "existence of additive identity element" property is not satisfied
• Distributivity of multiplication over addition for all natural numbers a, b, and c, a × (b + c) = (a × b) + (a × c).
• No nonzero zero divisors: if a and b are natural numbers such that a × b = 0, then a = 0 or b = 0 (or both).

Generalizations

Natural numbers are broadly used in two ways: to quantify and to order. A number used to represent the quantity of objects in a collection ("there are 6 coins on the table") is called a cardinal numeral, while a number used to order individual objects within a collection ("she finished 6th in the race") is an ordinal numeral.

These two uses of natural numbers apply only to finite sets. Georg Cantor discovered at the end of the 19th century that both uses of natural numbers can be generalized to infinite sets, but that they lead to two different concepts of "infinite" numbers, the cardinal numbers and the ordinal numbers.

Other generalizations of natural numbers are discussed in Number § Extensions of the concept.

See also

• Mathematics portal

• Canonical representation of a positive integer – Representation of a number as a product of primes
• Countable set – Mathematical set that can be enumerated
• Sequence – Function of the natural numbers in another set
• Ordinal number – Generalization of "n-th" to infinite cases
• Cardinal number – Size of a possibly infinite set
• Set-theoretic definition of natural numbers – Axiom(s) of Set Theory

Set inclusions between the natural numbers (ℕ), the integers (ℤ), the rational numbers (ℚ), the real numbers (ℝ), and the complex numbers (ℂ)

Notes

1. It depends on authors and context whether 0 is considered a natural number.
2. Older texts have occasionally employed J as the symbol for this set.^[12]
3. A tablet found at Kish ... thought to date from around 700 BC, uses three hooks to denote an empty place in the positional notation. Other tablets dated from around the same time use a single hook for an empty place.^[23]
4. This convention is used, for example, in Euclid's Elements, see D. Joyce's web edition of Book VII.^[27]
5. The English translation is from Gray. In a footnote, Gray attributes the German quote to: "Weber 1891–1892, 19, quoting from a lecture of Kronecker's of 1886."^[42][43]
6. "Much of the mathematical work of the twentieth century has been devoted to examining the logical foundations and structure of the subject." (Eves 1990, p. 606)
7. Hamilton (1988, pp. 117 ff) calls them "Peano's Postulates" and begins with "1.  0 is a natural number."
   Halmos (1974, p. 46) uses the language of set theory instead of the language of arithmetic for his five axioms. He begins with "(I)  0 ∈ ω (where, of course, 0 = ∅" (ω is the set of all natural numbers).
   Morash (1991) gives "a two-part axiom" in which the natural numbers begin with 1. (Section 10.1: An Axiomatization for the System of Positive Integers)