Ellingham–Horton graph
From Wikipedia, the free encyclopedia
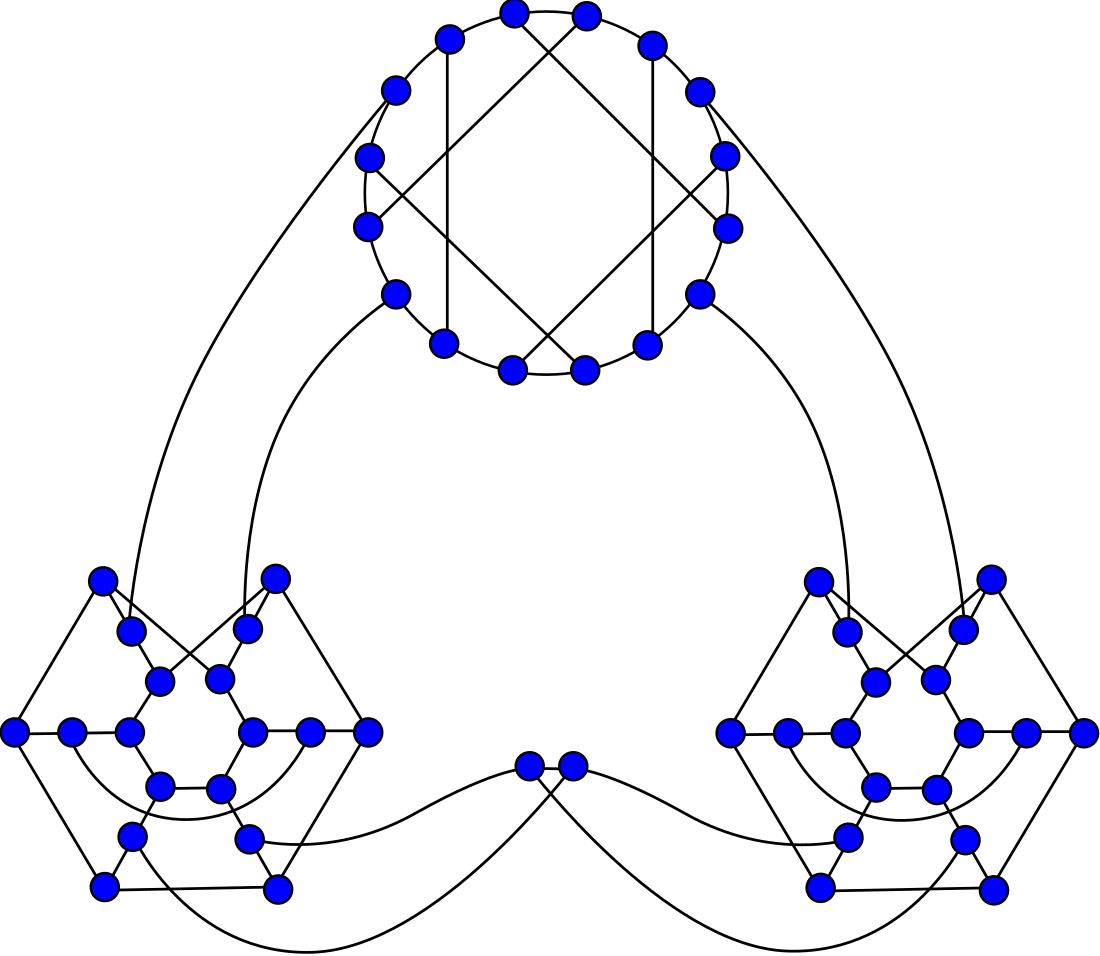
In the mathematical field of graph theory, the Ellingham–Horton graphs are two 3-regular graphs on 54 and 78 vertices: the Ellingham–Horton 54-graph and the Ellingham–Horton 78-graph.[1] They are named after Joseph D. Horton and Mark N. Ellingham, their discoverers. These two graphs provide counterexamples to the conjecture of W. T. Tutte that every cubic 3-connected bipartite graph is Hamiltonian.[2] The book thickness of the Ellingham-Horton 54-graph and the Ellingham-Horton 78-graph is 3 and the queue numbers 2.[3]
| Ellingham–Horton graphs | |
|---|---|
The Ellingham–Horton 54-graph. | |
| Named after | Joseph Horton and Mark Ellingham |
| Vertices | 54 (54-graph) 78 (78-graph) |
| Edges | 81 (54-graph) 117 (78-graph) |
| Radius | 9 (54-graph) 7 (78-graph) |
| Diameter | 10 (54-graph) 13 (78-graph) |
| Girth | 6 (both) |
| Automorphisms | 32 (54-graph) 16 (78-graph) |
| Chromatic number | 2 (both) |
| Chromatic index | 3 (both) |
| Book thickness | 3 (both) |
| Queue number | 2 (both) |
| Properties | Cubic (both) Bipartite (both) Regular (both) |
| Table of graphs and parameters | |
The first counterexample to the Tutte conjecture was the Horton graph, published by Bondy & Murty (1976).[4] After the Horton graph, a number of smaller counterexamples to the Tutte conjecture were found. Among them are a 92-vertex graph by Horton (1982),[5] a 78-vertex graph by Owens (1983),[6] and the two Ellingham–Horton graphs.
The first Ellingham–Horton graph was published by Ellingham (1981) and is of order 78.[7] At that time it was the smallest known counterexample to the Tutte conjecture. The second Ellingham–Horton graph was published by Ellingham & Horton (1983) and is of order 54.[8] In 1989, Georges' graph, the smallest currently-known Non-Hamiltonian 3-connected cubic bipartite graph was discovered, containing 50 vertices.[9]
Gallery
The chromatic number of the Ellingham–Horton 54-graph is 2.
The chromatic index of the Ellingham–Horton 54-graph is 3.
The chromatic number of the Ellingham–Horton 78-graph is 2.
The chromatic index of the Ellingham–Horton 78-graph is 3.
References
Wikiwand - on
Seamless Wikipedia browsing. On steroids.