Harries–Wong graph

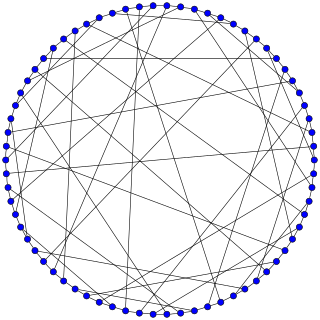
In the mathematical field of graph theory, the Harries–Wong graph is a 3-regular undirected graph with 70 vertices and 105 edges.^[1]

Harries–Wong graph
The Harries–Wong graph
Named after	W. Harries, Pak-Ken Wong
Vertices	70
Edges	105
Radius	6
Diameter	6
Girth	10
Automorphisms	24 (S4)
Chromatic number	2
Chromatic index	3
Genus	9
Book thickness	3
Queue number	2
Properties	Cubic Cage Triangle-free Hamiltonian
Table of graphs and parameters

The Harries–Wong graph has chromatic number 2, chromatic index 3, radius 6, diameter 6, girth 10 and is Hamiltonian. It is also a 3-vertex-connected and 3-edge-connected non-planar cubic graph. It has book thickness 3 and queue number 2.^[2]

The characteristic polynomial of the Harries–Wong graph is

${\displaystyle (x-3)(x-1)^{4}(x+1)^{4}(x+3)(x^{2}-6)(x^{2}-2)(x^{4}-6x^{2}+2)^{5}(x^{4}-6x^{2}+3)^{4}(x^{4}-6x^{2}+6)^{5}.\,}$

History

In 1972, A. T. Balaban published a (3-10)-cage graph, a cubic graph that has as few vertices as possible for girth 10.^[3] It was the first (3-10)-cage discovered but it was not unique.^[4]

The complete list of (3-10)-cages and the proof of minimality was given by O'Keefe and Wong in 1980.^[5] There exist three distinct (3-10)-cage graphs—the Balaban 10-cage, the Harries graph and the Harries–Wong graph.^[6] Moreover, the Harries–Wong graph and Harries graph are cospectral graphs.

Gallery

• 
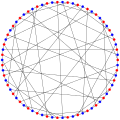
  The chromatic number of the Harries–Wong graph is 2.
• 
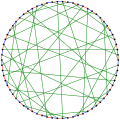
  The chromatic index of the Harries–Wong graph is 3.
• 
  Alternative drawing of the Harries–Wong graph.
• 
  The 8 orbits of the Harries–Wong graph.