Top Qs
Timeline
Chat
Perspective
Hemicube (geometry)
Abstract regular polyhedron with 3 square faces From Wikipedia, the free encyclopedia
Remove ads
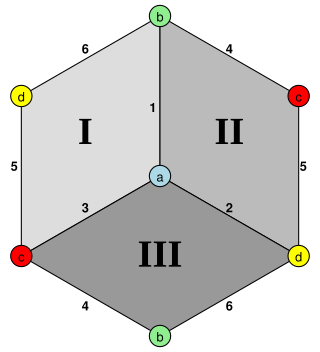
In abstract geometry, a hemicube is an abstract, regular polyhedron,[citation needed] produced by cutting a cube in half with a plane that passes through 2 opposite corners and the midpoints of 2 edges.[1]
This article needs additional citations for verification. (March 2025) |
A hemicube is also sometimes called a square hemiprism.[2]
Remove ads
Realization
It can be realized as a projective polyhedron (a tessellation of the real projective plane by three quadrilaterals), which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing the hemisphere into three equal parts.
It has three square faces, six edges, and four vertices. It has an unexpected property that every face is in contact with every other face on two edges, and every face contains all the vertices, which gives an example of an abstract polytope whose faces are not determined by their vertex sets.
From the point of view of graph theory the skeleton is a tetrahedral graph, an embedding of K4 (the complete graph with four vertices) on a projective plane.
The hemicube should not be confused with the demicube – the hemicube is a projective polyhedron, while the demicube is an ordinary polyhedron (in Euclidean space). While they both have half the vertices of a cube, the hemicube is a quotient of the cube, while the vertices of the demicube are a subset of the vertices of the cube.
Remove ads
Related polytopes
The hemicube is the Petrie dual to the regular tetrahedron, with the four vertices, six edges of the tetrahedron, and three Petrie polygon quadrilateral faces. The faces can be seen as red, green, and blue edge colorings in the tetrahedral graph:
See also
Footnotes
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads