Korteweg–De Vries equation

In mathematics, the Korteweg–De Vries (KdV) equation is a partial differential equation (PDE) which serves as a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an integrable PDE, exhibiting typical behaviors such as a large number of explicit solutions, in particular soliton solutions, and an infinite number of conserved quantities, despite the nonlinearity which typically renders PDEs intractable. The KdV can be solved by the inverse scattering method (ISM).^[3] In fact, Clifford Gardner, John M. Greene, Martin Kruskal and Robert Miura developed the classical inverse scattering method to solve the KdV equation.

Cnoidal wave solution to the Korteweg–De Vries equation, in terms of the square of the Jacobi elliptic function cn (and with value of the parameter m = 0.9).

Numerical solution of the KdV equation u_t + uu_x + δ²u_xxx = 0 (δ = 0.022) with an initial condition u(x, 0) = cos(πx). Time evolution was done by the Zabusky–Kruskal scheme.^[1] The initial cosine wave evolves into a train of solitary-type waves.

Two soliton solutions of the KdV equation interacting (purple) emphasizing the phase shift that occurs between them as they pass through each other. The red and blue solutions show the motion of individual solitons in the absence of the other^[2].

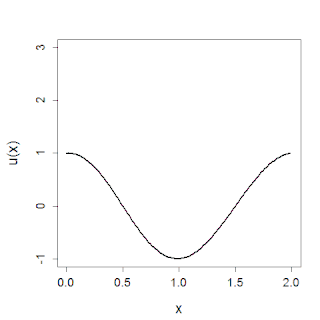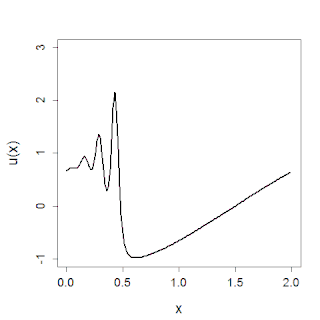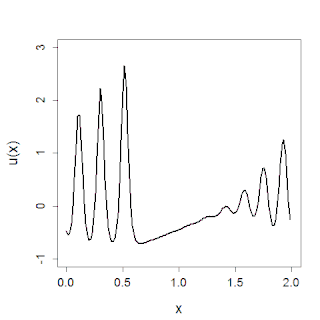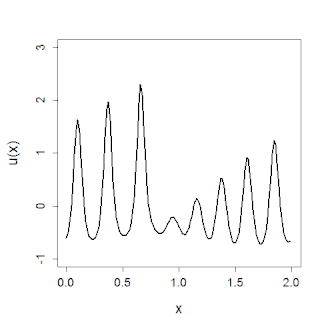
The KdV equation was first introduced by Joseph Valentin Boussinesq (1877, footnote on page 360) and rediscovered by Diederik Korteweg and Gustav de Vries in 1895, who found the simplest solution, the one-soliton solution.^[4][5] Understanding of the equation and behavior of solutions was greatly advanced by the computer simulations of Norman Zabusky and Kruskal in 1965 and then the development of the inverse scattering transform in 1967.

In 1972, T. Kawahara proposed a fifth-order KdV type of equation, known as Kawahara equation, that describes dispersive waves, particularly in cases when the coefficient of the KdV equation becomes very small or zero.^[6]

Definition

The KdV equation is a partial differential equation that models (spatially) one-dimensional nonlinear dispersive nondissipative waves described by a function ${\displaystyle \phi (x,t)}$ adhering to:^[7]

${\displaystyle \partial _{t}\phi +\partial _{x}^{3}\phi -6\,\phi \,\partial _{x}\phi =0\,\quad x\in \mathbb {R} ,\;t\geq 0,}$

where ${\displaystyle \partial _{x}^{3}\phi }$ accounts for dispersion and the nonlinear element ${\displaystyle \phi \partial _{x}\phi }$ is an advection term.

For modelling shallow water waves, ${\displaystyle \phi }$ is the height displacement of the water surface from its equilibrium height.

The constant ${\displaystyle 6}$ in front of the last term is conventional but of no great significance: multiplying ${\displaystyle t}$, ${\displaystyle x}$, and ${\displaystyle \phi }$ by constants can be used to make the coefficients of any of the three terms equal to any given non-zero constants.

Soliton solutions

One-soliton solution

Consider solutions in which a fixed waveform, given by ${\displaystyle f(X)}$, maintains its shape as it travels to the right at phase speed ${\displaystyle c}$. Such a solution is given by ${\displaystyle \varphi (x,t)=f(x-ct-a)=f(X)}$. Substituting it into the KdV equation gives the ordinary differential equation

${\displaystyle -c{\frac {df}{dX}}+{\frac {d^{3}f}{dX^{3}}}-6f{\frac {df}{dX}}=0,}$

or, integrating with respect to ${\displaystyle X}$,

${\displaystyle -cf+{\frac {d^{2}f}{dX^{2}}}-3f^{2}=A}$

where ${\displaystyle A}$ is a constant of integration. Interpreting the independent variable ${\displaystyle X}$ above as a virtual time variable, this means ${\displaystyle f}$ satisfies Newton's equation of motion of a particle of unit mass in a cubic potential

${\displaystyle V(f)=-\left(f^{3}+{\frac {1}{2}}cf^{2}+Af\right)}$.

If

${\displaystyle A=0,\,c>0}$

then the potential function ${\displaystyle V(f)}$ has local maximum at ${\displaystyle f=0}$; there is a solution in which ${\displaystyle f(X)}$ starts at this point at 'virtual time' ${\displaystyle -\infty }$, eventually slides down to the local minimum, then back up the other side, reaching an equal height, and then reverses direction, ending up at the local maximum again at time ${\displaystyle \infty }$. In other words, ${\displaystyle f(X)}$ approaches ${\displaystyle 0}$ as ${\displaystyle X\to -\infty }$. This is the characteristic shape of the solitary wave solution.

More precisely, the solution is

${\displaystyle \phi (x,t)=-{\frac {1}{2}}\,c\,\operatorname {sech} ^{2}\left[{{\sqrt {c}} \over 2}(x-c\,t-a)\right]}$

where ${\displaystyle \operatorname {sech} }$ stands for the hyperbolic secant and ${\displaystyle a}$ is an arbitrary constant.^[8] This describes a right-moving soliton with velocity ${\displaystyle c}$.

N-soliton solution

There is a known expression for a solution which is an ${\displaystyle N}$-soliton solution, which at late times resolves into ${\displaystyle N}$ separate single solitons.^[9] The solution depends on a set of decreasing positive parameters ${\displaystyle \chi _{1}>\cdots >\chi _{N}>0}$ and a set of non-zero parameters ${\displaystyle \beta _{1},\cdots ,\beta _{N}}$. The solution is given in the form $${\displaystyle \phi (x,t)=-2{\frac {\partial ^{2}}{\partial x^{2}}}\mathrm {log} [\mathrm {det} A(x,t)]}$$ where the components of the matrix ${\displaystyle A(x,t)}$ are ${\displaystyle A_{nm}(x,t)=\delta _{nm}+{\frac {\beta _{n}e^{8\chi _{n}^{3}t}e^{-(\chi _{n}+\chi _{m})x}}{\chi _{n}+\chi _{m}}}.}$

This is derived using the inverse scattering method.

Integrals of motion

The KdV equation has infinitely many integrals of motion, functionals on a solution ${\displaystyle \phi (t)}$ which do not change with time.^[10] They can be given explicitly as

${\displaystyle \int _{-\infty }^{+\infty }P_{2n-1}(\phi ,\,\partial _{x}\phi ,\,\partial _{x}^{2}\phi ,\,\ldots )\,{\text{d}}x\,}$

where the polynomials ${\displaystyle P_{n}}$ are defined recursively by

${\displaystyle {\begin{aligned}P_{1}&=\phi ,\\P_{n}&=-{\frac {dP_{n-1}}{dx}}+\sum _{i=1}^{n-2}\,P_{i}\,P_{n-1-i}\quad {\text{ for }}n\geq 2.\end{aligned}}}$

The first few integrals of motion are:

• the mass ${\displaystyle \int \phi \,\mathrm {d} x,}$
• the momentum ${\displaystyle \int \phi ^{2}\,\mathrm {d} x,}$
• the energy ${\displaystyle \int \left[2\phi ^{3}-\left(\partial _{x}\phi \right)^{2}\right]\,\mathrm {d} x}$.

Only the odd-numbered terms ${\displaystyle P_{2n+1}}$ result in non-trivial (meaning non-zero) integrals of motion.^[11]

Lax pairs

The KdV equation

${\displaystyle \partial _{t}\phi =6\,\phi \,\partial _{x}\phi -\partial _{x}^{3}\phi }$

can be reformulated as the Lax equation

${\displaystyle L_{t}=[L,A]\equiv LA-AL\,}$

with ${\displaystyle L}$ a Sturm–Liouville operator:

${\displaystyle {\begin{aligned}L&=-\partial _{x}^{2}+\phi ,\\A&=4\partial _{x}^{3}-6\phi \,\partial _{x}-3[\partial _{x},\phi ]\end{aligned}}}$

where ${\displaystyle [\partial _{x},\phi ]}$ is the commutator such that ${\displaystyle [\partial _{x},\phi ]f=f\partial _{x}\phi }$.^[12] The Lax pair accounts for the infinite number of first integrals of the KdV equation.^[13]

In fact, ${\displaystyle L}$ is the time-independent Schrödinger operator (disregarding constants) with potential ${\displaystyle \phi (x,t)}$. It can be shown that due to this Lax formulation that in fact the eigenvalues do not depend on ${\displaystyle t}$.^[14]

Zero-curvature representation

Setting the components of the Lax connection to be $${\displaystyle L_{x}={\begin{pmatrix}0&1\\\phi -\lambda &0\end{pmatrix}},L_{t}={\begin{pmatrix}-\phi _{x}&2\phi +4\lambda \\2\phi ^{2}-\phi _{xx}+2\phi \lambda -4\lambda ^{2}&\phi _{x}\end{pmatrix}},}$$ the KdV equation is equivalent to the zero-curvature equation for the Lax connection, $${\displaystyle \partial _{t}L_{x}-\partial _{x}L_{t}+[L_{x},L_{t}]=0.}$$

Least action principle

The Korteweg–De Vries equation

${\displaystyle \partial _{t}\phi +6\phi \,\partial _{x}\phi +\partial _{x}^{3}\phi =0,}$

is the Euler–Lagrange equation of motion derived from the Lagrangian density, ${\displaystyle {\mathcal {L}}\,}$

${\displaystyle {\mathcal {L}}:={\frac {1}{2}}\partial _{x}\psi \,\partial _{t}\psi +\left(\partial _{x}\psi \right)^{3}-{\frac {1}{2}}\left(\partial _{x}^{2}\psi \right)^{2}}$

1

with ${\displaystyle \phi }$ defined by

${\displaystyle \phi$ :={\frac {\partial \psi }{\partial x}}.}

Derivation of Euler–Lagrange equations

Since the Lagrangian (eq (1)) contains second derivatives, the Euler–Lagrange equation of motion for this field is

${\displaystyle \partial _{\mu \mu }\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{\mu \mu }\psi )}}\right)-\partial _{\mu }\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{\mu }\psi )}}\right)+{\frac {\partial {\mathcal {L}}}{\partial \psi }}=0.}$

2

where ${\displaystyle \partial }$ is a derivative with respect to the ${\displaystyle \mu }$ component.

A sum over ${\displaystyle \mu }$ is implied so eq (2) really reads,

${\displaystyle \partial _{tt}\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{tt}\psi )}}\right)+\partial _{xx}\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{xx}\psi )}}\right)-\partial _{t}\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{t}\psi )}}\right)-\partial _{x}\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{x}\psi )}}\right)+{\frac {\partial {\mathcal {L}}}{\partial \psi }}=0.}$

3

Evaluate the five terms of eq (3) by plugging in eq (1),

${\displaystyle \partial _{tt}\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{tt}\psi )}}\right)=0}$

${\displaystyle \partial _{xx}\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{xx}\psi )}}\right)=\partial _{xx}\left(-\partial _{xx}\psi \right)}$

${\displaystyle \partial _{t}\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{t}\psi )}}\right)=\partial _{t}\left({\frac {1}{2}}\partial _{x}\psi \right)}$

${\displaystyle \partial _{x}\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{x}\psi )}}\right)=\partial _{x}\left({\frac {1}{2}}\partial _{t}\psi +3(\partial _{x}\psi )^{2}\right)\,}$

${\displaystyle {\frac {\partial {\mathcal {L}}}{\partial \psi }}=0}$

Remember the definition ${\displaystyle \phi =\partial _{x}\psi }$, so use that to simplify the above terms,

${\displaystyle \partial _{xx}\left(-\partial _{xx}\psi \right)=-\partial _{xxx}\phi }$

${\displaystyle \partial _{t}\left({\frac {1}{2}}\partial _{x}\psi \right)={\frac {1}{2}}\partial _{t}\phi }$

${\displaystyle \partial _{x}\left({\frac {1}{2}}\partial _{t}\psi +3(\partial _{x}\psi )^{2}\right)={\frac {1}{2}}\partial _{t}\phi +3\partial _{x}(\phi )^{2}={\frac {1}{2}}\partial _{t}\phi +6\phi \partial _{x}\phi }$

Finally, plug these three non-zero terms back into eq (3) to see

${\displaystyle \left(-\partial _{xxx}\phi \right)-\left({\frac {1}{2}}\partial _{t}\phi \right)-\left({\frac {1}{2}}\partial _{t}\phi +6\phi \partial _{x}\phi \right)=0,}$

which is exactly the KdV equation

${\displaystyle \partial _{t}\phi +6\phi \,\partial _{x}\phi +\partial _{x}^{3}\phi =0.}$

Long-time asymptotics

It can be shown that any sufficiently fast decaying smooth solution will eventually split into a finite superposition of solitons travelling to the right plus a decaying dispersive part travelling to the left. This was first observed by Zabusky & Kruskal (1965) and can be rigorously proven using the nonlinear steepest descent analysis for oscillatory Riemann–Hilbert problems.^[15]

History

The history of the KdV equation started with experiments by John Scott Russell in 1834, followed by theoretical investigations by Lord Rayleigh and Joseph Boussinesq around 1870 and, finally, Korteweg and De Vries in 1895.

The KdV equation was not studied much after this until Zabusky & Kruskal (1965) discovered numerically that its solutions seemed to decompose at large times into a collection of "solitons": well separated solitary waves. Moreover, the solitons seems to be almost unaffected in shape by passing through each other (though this could cause a change in their position). They also made the connection to earlier numerical experiments by Fermi, Pasta, Ulam, and Tsingou by showing that the KdV equation was the continuum limit of the FPUT system. Development of the analytic solution by means of the inverse scattering transform was done in 1967 by Gardner, Greene, Kruskal and Miura.^[3][16]

The KdV equation is now seen to be closely connected to Huygens' principle.^[17][18]

Applications and connections

The KdV equation has several connections to physical problems. In addition to being the governing equation of the string in the Fermi–Pasta–Ulam–Tsingou problem in the continuum limit, it approximately describes the evolution of long, one-dimensional waves in many physical settings, including:

• shallow-water waves with weakly non-linear restoring forces,
• long internal waves in a density-stratified ocean,
• ion acoustic waves in a plasma,
• acoustic waves on a crystal lattice.

The KdV equation can also be solved using the inverse scattering transform such as those applied to the non-linear Schrödinger equation.

KdV equation and the Gross–Pitaevskii equation

Considering the simplified solutions of the form

${\displaystyle \phi (x,t)=\phi (x\pm t)}$

we obtain the KdV equation as

${\displaystyle \pm \partial _{x}\phi +\partial _{x}^{3}\phi +6\,\phi \,\partial _{x}\phi =0\,}$

or

${\displaystyle \pm \partial _{x}\phi +\partial _{x}(\partial _{x}^{2}\phi +3\phi ^{2})=0\,}$

Integrating and taking the special case in which the integration constant is zero, we have:

${\displaystyle -\partial _{x}^{2}\phi -3\phi ^{2}=\pm \phi \,}$

which is the ${\displaystyle \lambda =1}$ special case of the generalized stationary Gross–Pitaevskii equation (GPE)

${\displaystyle -\partial _{x}^{2}\phi -3\phi ^{\lambda }\phi =\pm \phi \,}$

Therefore, for the certain class of solutions of generalized GPE (${\displaystyle \lambda =4}$ for the true one-dimensional condensate and ${\displaystyle \lambda =2}$ while using the three dimensional equation in one dimension), two equations are one. Furthermore, taking the ${\displaystyle \lambda =3}$ case with the minus sign and the ${\displaystyle \phi }$ real, one obtains an attractive self-interaction that should yield a bright soliton.^{[citation needed]}

Variations

Many different variations of the KdV equations have been studied. Some are listed in the following table.

Name	Equation
Korteweg–De Vries (KdV)	${\displaystyle \displaystyle \partial _{t}u+\partial _{x}^{3}u+6u\partial _{x}u=0}$
KdV (cylindrical)	${\displaystyle \displaystyle \partial _{t}u+\partial _{x}^{3}u-6u\partial _{x}u+{\tfrac {1}{2t}}u=0}$
KdV (deformed)	${\displaystyle \displaystyle \partial _{t}u+\partial _{x}\left({\frac {\partial _{x}^{2}u-2\eta u^{3}-3u(\partial _{x}u)^{2}}{2(\eta +u^{2})}}\right)=0}$
KdV (generalized)	${\displaystyle \displaystyle \partial _{t}u+\partial _{x}^{3}u=\partial _{x}^{5}u}$
KdV (generalized)	${\displaystyle \displaystyle \partial _{t}u+\partial _{x}^{3}u+\partial _{x}f(u)=0}$
KdV (modified)	${\displaystyle \displaystyle \partial _{t}u+\partial _{x}^{3}u\pm 6u^{2}\partial _{x}u=0}$
Gardner equation	${\displaystyle \displaystyle \partial _{t}u+\partial _{x}^{3}u-(6\varepsilon ^{2}u^{2}+6u)\partial _{x}u=0}$
KdV (modified modified)	${\displaystyle \displaystyle \partial _{t}u+\partial _{x}^{3}u-{\tfrac {1}{8}}(\partial _{x}u)^{3}+(\partial _{x}u)(Ae^{au}+B+Ce^{-au})=0}$
KdV (spherical)	${\displaystyle \displaystyle \partial _{t}u+\partial _{x}^{3}u-6u\partial _{x}u+{\tfrac {1}{t}}u=0}$
Hirota–Satsuma equation	${\displaystyle \displaystyle {\begin{cases}u_{t}-{\frac {1}{2}}u_{xxx}+3uu_{x}-3(vw)_{x}=0\\v_{t}+v_{xxx}-3uv_{x}=0\\w_{t}+w_{xxx}-3uw_{x}=0\end{cases}}}$
KdV (super)	${\displaystyle \displaystyle {\begin{cases}\partial _{t}u=6u\partial _{x}u-\partial _{x}^{3}u+3w\partial _{x}^{2}w\\\partial _{t}w=3(\partial _{x}u)w+6u\partial _{x}w-4\partial _{x}^{3}w\end{cases}}}$
KdV (transitional)	${\displaystyle \displaystyle \partial _{t}u+\partial _{x}^{3}u-6f(t)u\partial _{x}u=0}$
KdV (variable coefficients)	${\displaystyle \displaystyle \partial _{t}u+\beta t^{n}\partial _{x}^{3}u+\alpha t^{n}u\partial _{x}u=0}$
KdV-Burgers equation	${\displaystyle \displaystyle \partial _{t}u+\mu \partial _{x}^{3}u+u\partial _{x}u-\nu \partial _{x}^{2}u=0}$
Kawahara equation	${\displaystyle \partial _{t}u+\alpha u\partial _{x}u+\beta \partial _{x}^{3}u-\gamma \,\partial _{x}^{5}u=0,}$
non-homogeneous KdV	${\displaystyle \partial _{t}u+\alpha u+\beta \partial _{x}u+\gamma \partial _{x}^{2}u=Ai(x),\quad u(x,0)=f(x)}$

See also

• Advection-diffusion equation
• Benjamin–Bona–Mahony equation
• Boussinesq approximation (water waves)
• Cnoidal wave
• Dispersion (water waves)
• Dispersionless equation
• Fifth-order Korteweg–De Vries equation
• Kadomtsev–Petviashvili equation
• KdV hierarchy
• Modified KdV–Burgers equation
• Novikov–Veselov equation
• Schamel equation
• Ursell number
• Vector soliton