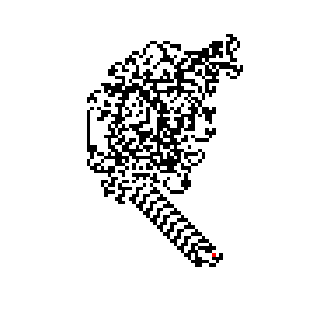Top Qs
Timeline
Chat
Perspective
Langton's ant
Two-dimensional Turing machine with emergent behavior From Wikipedia, the free encyclopedia
Remove ads
Langton's ant is a two-dimensional Turing machine with a very simple set of rules but complex emergent behavior. It was invented by Chris Langton in 1986 and runs on a square lattice of black and white cells.[1] The idea has been generalized in several different ways, such as turmites which add more colors and more states.

Remove ads
Rules

Squares on a plane are colored variously either black or white. We arbitrarily identify one square as the "ant". The ant can travel in any of the four cardinal directions at each step it takes. The "ant" moves according to the rules below:
- At a white square, turn 90° clockwise, flip the color of the square, move forward one unit
- At a black square, turn 90° counter-clockwise, flip the color of the square, move forward one unit
Langton's ant can also be described as a cellular automaton, where the grid is colored black or white and the "ant" square has one of eight different colors assigned to encode the combination of black/white state and the current direction of motion of the ant.[2]
Remove ads
Modes of behavior
These simple rules lead to complex behavior. Three distinct modes of behavior are apparent,[3] when starting on a completely white grid.
- Simplicity. During the first few hundred moves it creates very simple patterns which are often symmetric.
- Chaos. After a few hundred moves, a large, irregular pattern of black and white squares appears. The ant traces a pseudo-random path until around 10,000 steps.
- Emergent order. Finally the ant starts building a recurrent "highway" pattern of 104 steps that repeats indefinitely.
All finite initial configurations tested eventually converge to the same repetitive pattern, suggesting that the "highway" is an attractor of Langton's ant, but no one has been able to prove that this is true for all such initial configurations. It is only known that the ant's trajectory is always unbounded regardless of the initial configuration[4] – this result was incorrectly attributed and is known as the Cohen-Kong theorem.[5]
Remove ads
Computational properties
In 2000, Gajardo et al. showed a construction that calculates any boolean circuit using the trajectory of a single instance of Langton's ant.[2]
Extension to multiple colors
Summarize
Perspective
Greg Turk and Jim Propp considered a simple extension to Langton's ant where instead of just two colors, more colors are used.[6] The colors are modified in a cyclic fashion. A simple naming scheme is used: for each of the successive colors, a letter "L" or "R" is used to indicate whether a left or right turn should be taken. Langton's ant has the name "RL" in this naming scheme.
Some of these extended Langton's ants produce patterns that become symmetric over and over again. One of the simplest examples is the ant "RLLR". One sufficient condition for this to happen is that the ant's name, seen as a cyclic list, consists of consecutive pairs of identical letters "LL" or "RR". The proof involves Truchet tiles.
- Some example patterns in the multiple-color extension of Langton's ants:
- RLR: Grows chaotically. It is not known whether this ant ever produces a highway.
- LLRR: Grows symmetrically.
- LRRRRRLLR: Fills space in a square around itself.
- LLRRRLRLRLLR: Creates a convoluted highway.
- RRLLLRLLLRRR: Creates a filled triangle shape that grows and moves after 15900~ iterations.
- L2NNL1L2L1: Hexagonal grid, grows circularly.
- L1L2NUL2L1R2: Hexagonal grid, spiral growth.
- R1R2NUR2R1L2: Animation.
The hexagonal grid permits up to six different rotations, which are notated here as N (no change), R1 (60° clockwise), R2 (120° clockwise), U (180°), L2 (120° counter-clockwise), L1 (60° counter-clockwise).
Remove ads
Extension to multiple states
A further extension of Langton's ants is to consider multiple states of the Turing machine – as if the ant itself has a color that can change. These ants are called turmites, a contraction of "Turing machine termites". Common behaviours include the production of highways, chaotic growth and spiral growth.[7]
- Some example turmites:
- Spiral growth.
- Semi-chaotic growth.
- Production of a highway after a period of chaotic growth.
- Chaotic growth with a distinctive texture.
- Growth with a distinctive texture inside an expanding frame.
- Constructing a Fibonacci spiral.
- Constructing a growing diamond
Remove ads
Extension to multiple ants
Multiple Langton's ants can co-exist on the 2D plane, and their interactions give rise to complex, higher-order automata that collectively build a wide variety of organized structures.
There are different ways of modelling their interaction and the results of the simulation may strongly depend on the choices made.[8]
Multiple turmites can co-exist on the 2D plane as long as there is a rule that defines what happens when they meet. Ed Pegg, Jr. considered ants that can turn for example both left and right, splitting in two and annihilating each other when they meet.[9]
Remove ads
See also
- Conway's Game of Life – Two-dimensional cellular automaton
- Langton's loops – Self-reproducing cellular automaton patterns
- Paterson's worms – Family of cellular automata to model feeding behaviour
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads