Legendre's constant

Legendre's constant is a mathematical constant occurring in a formula constructed by Adrien-Marie Legendre to approximate the behavior of the prime-counting function ${\displaystyle \pi (x)}$. The value that corresponds precisely to its asymptotic behavior is now known to be 1.

The first 100,000 elements of the sequence a_n = log(n) − n/π(n) (red line) appear to converge to a value around 1.08366 (blue line).

Later elements up to 10,000,000 of the same sequence a_n = log(n) − n/π(n) (red line) appear to be consistently less than 1.08366 (blue line).

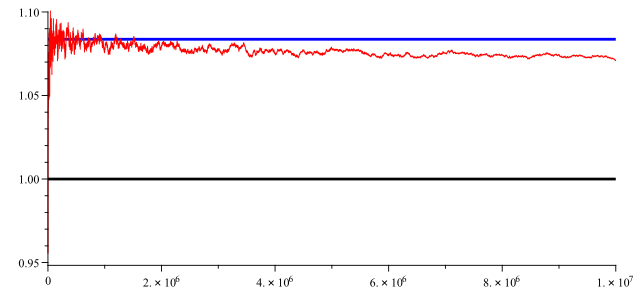
Examination of available numerical data for known values of ${\displaystyle \pi (x)}$ led Legendre to an approximating formula.

Legendre proposed in 1808 the formula $${\displaystyle y={\frac {x}{\log(x)-1.08366}},}$$ (OEIS: A228211), as giving an approximation of ${\displaystyle y=\pi (x)}$ with a "very satisfying precision".^[1][2]

However, if one defines the real function ${\displaystyle B(x)}$ by $${\displaystyle \pi (x)={\frac {x}{\log(x)-B(x)}},}$$ and if ${\displaystyle B(x)}$ converges to a real constant ${\displaystyle B}$ as ${\displaystyle x}$ tends to infinity, then this constant satisfies $${\displaystyle B=\lim _{x\to \infty }\left(\log(x)-{x \over \pi (x)}\right).}$$

Not only is it now known that the limit exists, but also that its value is equal to 1, somewhat less than Legendre's 1.08366. Regardless of its exact value, the existence of the limit ${\displaystyle B}$ implies the prime number theorem.

Pafnuty Chebyshev proved in 1849^[3] that if the limit B exists, it must be equal to 1. An easier proof was given by Pintz in 1980.^[4]

It is an immediate consequence of the prime number theorem, under the precise form with an explicit estimate of the error term

$${\displaystyle \pi (x)=\operatorname {Li} (x)+O\left(xe^{-a{\sqrt {\log x}}}\right)\quad {\text{as }}x\to \infty }$$

(for some positive constant a, where O(...) is the big O notation), as proved in 1899 by Charles de La Vallée Poussin,^[5] that B indeed is equal to 1. (The prime number theorem had been proved in 1896, independently by Jacques Hadamard^[6] and La Vallée Poussin,^{[7]: 183–256, 281–361 [page needed]} but without any estimate of the involved error term).

Being evaluated to such a simple number has made the term Legendre's constant mostly only of historical value, with it often (technically incorrectly) being used to refer to Legendre's first guess 1.08366... instead.

Numerical values

Using known values for ${\displaystyle \pi (x)}$, we can compute ${\displaystyle B(x)=\log x-{\frac {x}{\pi (x)}}}$ for values of ${\displaystyle x}$ far beyond what was available to Legendre:

Legendre's constant asymptotically approaching 1 for large values of ${\displaystyle x}$

x	B(x)		x	B(x)		x	B(x)		x	B(x)
102	0.605170		1016	1.029660		1030	1.015148		1044	1.010176
103	0.955374		1017	1.027758		1031	1.014637		1045	1.009943
104	1.073644		1018	1.026085		1032	1.014159		1046	1.009720
105	1.087571		1019	1.024603		1033	1.013712		1047	1.009507
106	1.076332		1020	1.023281		1034	1.013292		1048	1.009304
107	1.070976		1021	1.022094		1035	1.012897		1049	1.009108
108	1.063954		1022	1.021022		1036	1.012525		1050	1.008921
109	1.056629		1023	1.020050		1037	1.012173		1051	1.008742
1010	1.050365		1024	1.019164		1038	1.011841		1052	1.008569
1011	1.045126		1025	1.018353		1039	1.011527		1053	1.008403
1012	1.040872		1026	1.017607		1040	1.011229		1054	1.008244
1013	1.037345		1027	1.016921		1041	1.010946		1055	1.008090
1014	1.034376		1028	1.016285		1042	1.010676		1056	1.007942
1015	1.031844		1029	1.015696		1043	1.010420		1057	1.007799

Values up to ${\displaystyle \pi (10^{29})}$ (the first two columns) are known exactly; the values in the third and fourth columns are estimated using the Riemann R function.