Liouville function

In number theory, the Liouville function, named after French mathematician Joseph Liouville and denoted ${\displaystyle \lambda (n)}$, is an important arithmetic function. Its value is ${\displaystyle 1}$ if ${\displaystyle n}$ is the product of an even number of prime numbers, and ${\displaystyle -1}$ if it is the product of an odd number of prime numbers.

Definition

By the fundamental theorem of arithmetic, any positive integer ${\displaystyle n}$ can be represented uniquely as a product of powers of primes:

${\displaystyle n=p_{1}^{a_{1}}\cdots p_{k}^{a_{k}}}$,

where ${\displaystyle p_{1},\dots ,p_{k}}$ are primes and the exponents ${\displaystyle a_{1},\dots ,a_{k}}$ are positive integers. The prime omega function ${\displaystyle \Omega (n)}$ counts the number of primes in the factorization of ${\displaystyle n}$ with multiplicity:

${\displaystyle \Omega (n)=a_{1}+a_{2}+\cdots +a_{k}}$.

Thus, the Liouville function is defined by

${\displaystyle \lambda (n)=(-1)^{\Omega (n)}}$

(sequence A008836 in the OEIS).

Properties

Since ${\displaystyle \Omega (n)}$ is completely additive; i.e., ${\displaystyle \Omega (ab)=\Omega (a)+\Omega (b)}$, then ${\displaystyle \lambda (n)}$ is completely multiplicative. Since ${\displaystyle 1}$ has no prime factors, ${\displaystyle \Omega (1)=0}$, so ${\displaystyle \lambda (1)=1}$.

${\displaystyle \lambda (n)}$ is also related to the Möbius function ${\displaystyle \mu (n)}$: if we write ${\displaystyle n}$ as ${\displaystyle n=a^{2}b}$, where ${\displaystyle b}$ is squarefree, then

${\displaystyle \lambda (n)=\mu (b).}$

The sum of the Liouville function over the divisors of ${\displaystyle n}$ is the characteristic function of the squares:

${\displaystyle \sum _{d|n}\lambda (d)={\begin{cases}1&{\text{if }}n{\text{ is a perfect square,}}\\0&{\text{otherwise.}}\end{cases}}}$

Möbius inversion of this formula yields

${\displaystyle \lambda (n)=\sum _{d^{2}|n}\mu \left({\frac {n}{d^{2}}}\right).}$

The Dirichlet inverse of the Liouville function is the absolute value of the Möbius function, ${\displaystyle \lambda ^{-1}(n)=|\mu (n)|=\mu ^{2}(n)}$, the characteristic function of the squarefree integers.

Series

The Dirichlet series for the Liouville function is related to the Riemann zeta function by

${\displaystyle {\frac {\zeta (2s)}{\zeta (s)}}=\sum _{n=1}^{\infty }{\frac {\lambda (n)}{n^{s}}}.}$

Also:

${\displaystyle \sum \limits _{n=1}^{\infty }{\frac {\lambda (n)\ln n}{n}}=-\zeta (2)=-{\frac {\pi ^{2}}{6}}.}$

The Lambert series for the Liouville function is

${\displaystyle \sum _{n=1}^{\infty }{\frac {\lambda (n)q^{n}}{1-q^{n}}}=\sum _{n=1}^{\infty }q^{n^{2}}={\frac {1}{2}}\left(\vartheta _{3}(q)-1\right),}$

where ${\displaystyle \vartheta _{3}(q)}$ is the Jacobi theta function.

Conjectures on weighted summatory functions

Summatory Liouville function L(n) up to n = 10⁴. The readily visible oscillations are due to the first non-trivial zero of the Riemann zeta function.

Summatory Liouville function L(n) up to n = 10⁷. Note the apparent scale invariance of the oscillations.

Logarithmic graph of the negative of the summatory Liouville function L(n) up to n = 2 × 10⁹. The green spike shows the function itself (not its negative) in the narrow region where the Pólya conjecture fails; the blue curve shows the oscillatory contribution of the first Riemann zero.

Harmonic Summatory Liouville function T(n) up to n = 10³

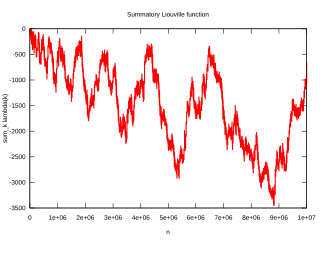
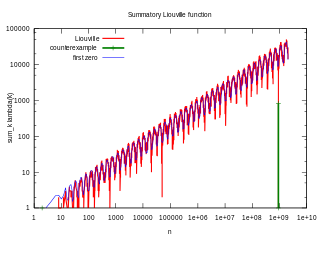
The Pólya problem is a question raised made by George Pólya in 1919. Defining

${\displaystyle L(n)=\sum _{k=1}^{n}\lambda (k)}$ (sequence A002819 in the OEIS),

the problem asks whether ${\displaystyle L(n)\leq 0}$ for some n > 1. The answer turns out to be yes. The smallest counter-example is n = 906150257, found by Minoru Tanaka in 1980. It has since been shown that L(n) > 0.0618672√n for infinitely many positive integers n,^[1] while it can also be shown via the same methods that L(n) < −1.3892783√n for infinitely many positive integers n.^[2]

For any ${\displaystyle \varepsilon >0}$, assuming the Riemann hypothesis, we have that the summatory function ${\displaystyle L(x)\equiv L_{0}(x)}$ is bounded by

${\displaystyle L(x)=O\left({\sqrt {x}}\exp \left(C\cdot \log ^{1/2}(x)\left(\log \log x\right)^{5/2+\varepsilon }\right)\right),}$

where the ${\displaystyle C>0}$ is some absolute limiting constant.^[2]

Define the related sum

${\displaystyle T(n)=\sum _{k=1}^{n}{\frac {\lambda (k)}{k}}.}$

It was open for some time whether T(n) ≥ 0 for sufficiently big n ≥ n₀ (this conjecture is occasionally—though incorrectly—attributed to Pál Turán). This was then disproved by Haselgrove (1958), who showed that T(n) takes negative values infinitely often. A confirmation of this positivity conjecture would have led to a proof of the Riemann hypothesis, as was shown by Pál Turán.

Generalizations

More generally, we can consider the weighted summatory functions over the Liouville function defined for any ${\displaystyle \alpha \in \mathbb {R} }$ as follows for positive integers x where (as above) we have the special cases ${\displaystyle L(x):=L_{0}(x)}$ and ${\displaystyle T(x)=L_{1}(x)}$ ^[2]

${\displaystyle L_{\alpha }(x):=\sum _{n\leq x}{\frac {\lambda (n)}{n^{\alpha }}}.}$

These ${\displaystyle \alpha ^{-1}}$-weighted summatory functions are related to the Mertens function, or weighted summatory functions of the Möbius function. In fact, we have that the so-termed non-weighted, or ordinary, function ${\displaystyle L(x)}$ precisely corresponds to the sum

${\displaystyle L(x)=\sum _{d^{2}\leq x}M\left({\frac {x}{d^{2}}}\right)=\sum _{d^{2}\leq x}\sum _{n\leq {\frac {x}{d^{2}}}}\mu (n).}$

Moreover, these functions satisfy similar bounding asymptotic relations.^[2] For example, whenever ${\displaystyle 0\leq \alpha \leq {\frac {1}{2}}}$, we see that there exists an absolute constant ${\displaystyle C_{\alpha }>0}$ such that

${\displaystyle L_{\alpha }(x)=O\left(x^{1-\alpha }\exp \left(-C_{\alpha }{\frac {(\log x)^{3/5}}{(\log \log x)^{1/5}}}\right)\right).}$

By an application of Perron's formula, or equivalently by a key (inverse) Mellin transform, we have that

${\displaystyle {\frac {\zeta (2\alpha +2s)}{\zeta (\alpha +s)}}=s\cdot \int _{1}^{\infty }{\frac {L_{\alpha }(x)}{x^{s+1}}}dx,}$

which then can be inverted via the inverse transform to show that for ${\displaystyle x>1}$, ${\displaystyle T\geq 1}$ and ${\displaystyle 0\leq \alpha <{\frac {1}{2}}}$

${\displaystyle L_{\alpha }(x)={\frac {1}{2\pi \imath }}\int _{\sigma _{0}-\imath T}^{\sigma _{0}+\imath T}{\frac {\zeta (2\alpha +2s)}{\zeta (\alpha +s)}}\cdot {\frac {x^{s}}{s}}ds+E_{\alpha }(x)+R_{\alpha }(x,T),}$

where we can take ${\displaystyle \sigma _{0}:=1-\alpha +1/\log(x)}$, and with the remainder terms defined such that ${\displaystyle E_{\alpha }(x)=O(x^{-\alpha })}$ and ${\displaystyle R_{\alpha }(x,T)\rightarrow 0}$ as ${\displaystyle T\rightarrow \infty }$.

In particular, if we assume that the Riemann hypothesis (RH) is true and that all of the non-trivial zeros, denoted by ${\displaystyle \rho ={\frac {1}{2}}+\imath \gamma }$, of the Riemann zeta function are simple, then for any ${\displaystyle 0\leq \alpha <{\frac {1}{2}}}$ and ${\displaystyle x\geq 1}$ there exists an infinite sequence of ${\displaystyle \{T_{v}\}_{v\geq 1}}$ which satisfies that ${\displaystyle v\leq T_{v}\leq v+1}$ for all v such that

${\displaystyle L_{\alpha }(x)={\frac {x^{1/2-\alpha }}{(1-2\alpha )\zeta (1/2)}}+\sum _{|\gamma |<T_{v}}{\frac {\zeta (2\rho )}{\zeta ^{\prime }(\rho )}}\cdot {\frac {x^{\rho -\alpha }}{(\rho -\alpha )}}+E_{\alpha }(x)+R_{\alpha }(x,T_{v})+I_{\alpha }(x),}$

where for any increasingly small ${\displaystyle 0<\varepsilon <{\frac {1}{2}}-\alpha }$ we define

${\displaystyle I_{\alpha }(x):={\frac {1}{2\pi \imath \cdot x^{\alpha }}}\int _{\varepsilon +\alpha -\imath \infty }^{\varepsilon +\alpha +\imath \infty }{\frac {\zeta (2s)}{\zeta (s)}}\cdot {\frac {x^{s}}{(s-\alpha )}}ds,}$

and where the remainder term

${\displaystyle R_{\alpha }(x,T)\ll x^{-\alpha }+{\frac {x^{1-\alpha }\log(x)}{T}}+{\frac {x^{1-\alpha }}{T^{1-\varepsilon }\log(x)}},}$

which of course tends to 0 as ${\displaystyle T\rightarrow \infty }$. These exact analytic formula expansions again share similar properties to those corresponding to the weighted Mertens function cases. Additionally, since ${\displaystyle \zeta (1/2)<0}$ we have another similarity in the form of ${\displaystyle L_{\alpha }(x)}$ to ${\displaystyle M(x)}$ insomuch as the dominant leading term in the previous formulas predicts a negative bias in the values of these functions over the positive natural numbers x.