List of spherical symmetry groups

Finite spherical symmetry groups are also called point groups in three dimensions. There are five fundamental symmetry classes which have triangular fundamental domains: dihedral, cyclic, tetrahedral, octahedral, and icosahedral symmetry.

Selected point groups in three dimensions

Involutional symmetry Cs, (*) [ ] =	Cyclic symmetry Cnv, (*nn) [n] =	Dihedral symmetry Dnh, (*n22) [n,2] =
Polyhedral group, [n,3], (*n32)
Tetrahedral symmetry Td, (*332) [3,3] =	Octahedral symmetry Oh, (*432) [4,3] =	Icosahedral symmetry Ih, (*532) [5,3] =

This article lists the groups by Schoenflies notation, Coxeter notation,^[1] orbifold notation,^[2] and order. John Conway uses a variation of the Schoenflies notation, based on the groups' quaternion algebraic structure, labeled by one or two upper case letters, and whole number subscripts. The group order is defined as the subscript, unless the order is doubled for symbols with a plus or minus, "±", prefix, which implies a central inversion.^[3]

Hermann–Mauguin notation (International notation) is also given. The crystallography groups, 32 in total, are a subset with element orders 2, 3, 4 and 6.^[4]

Involutional symmetry

There are four involutional groups: no symmetry (C₁), reflection symmetry (C_s), 2-fold rotational symmetry (C₂), and central point symmetry (C_i).

Intl	Geo	Orbifold	Schönflies	Conway	Coxeter		Order	Abstract	Fund. domain
1	1	11	C1	C1	][ [ ]+		1	Z1
2	2	22	D1 = C2	D2 = C2	[2]+		2	Z2
1	22	×	Ci = S2	CC2	[2+,2+]		2	Z2
2 = m	1	*	Cs = C1v = C1h	±C1 = CD2	[ ]		2	Z2

Cyclic symmetry

There are four infinite cyclic symmetry families, with n = 2 or higher. (n may be 1 as a special case as no symmetry)

Intl	Geo	Orbifold	Schönflies	Conway	Coxeter		Order	Abstract	Fund. domain
4	42	2×	S4	CC4	[2+,4+]		4	Z4
2/m	22	2*	C2h = D1d	±C2 = ±D2	[2,2+] [2+,2]		4	Z4

Intl	Geo	Orbifold	Schönflies	Conway	Coxeter		Order	Abstract	Fund. domain
2 3 4 5 6 n	2 3 4 5 6 n	22 33 44 55 66 nn	C2 C3 C4 C5 C6 Cn	C2 C3 C4 C5 C6 Cn	[2]+ [3]+ [4]+ [5]+ [6]+ [n]+		2 3 4 5 6 n	Z2 Z3 Z4 Z5 Z6 Zn
2mm 3m 4mm 5m 6mm nm (n is odd) nmm (n is even)	2 3 4 5 6 n	*22 *33 *44 *55 *66 *nn	C2v C3v C4v C5v C6v Cnv	CD4 CD6 CD8 CD10 CD12 CD2n	[2] [3] [4] [5] [6] [n]		4 6 8 10 12 2n	D4 D6 D8 D10 D12 D2n
3 8 5 12 -	62 82 10.2 12.2 2n.2	3× 4× 5× 6× n×	S6 S8 S10 S12 S2n	±C3 CC8 ±C5 CC12 CC2n / ±Cn	[2+,6+] [2+,8+] [2+,10+] [2+,12+] [2+,2n+]		6 8 10 12 2n	Z6 Z8 Z10 Z12 Z2n
3/m=6 4/m 5/m=10 6/m n/m	32 42 52 62 n2	3* 4* 5* 6* n*	C3h C4h C5h C6h Cnh	CC6 ±C4 CC10 ±C6 ±Cn / CC2n	[2,3+] [2,4+] [2,5+] [2,6+] [2,n+]		6 8 10 12 2n	Z6 Z2×Z4 Z10 Z2×Z6 Z2×Zn ≅Z2n (odd n)

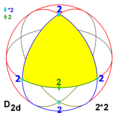
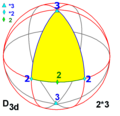
Dihedral symmetry

There are three infinite dihedral symmetry families, with n = 2 or higher (n may be 1 as a special case).

Intl	Geo	Orbifold	Schönflies	Conway	Coxeter	Order	Abstract	Fund. domain
222	2.2	222	D2	D4	[2,2]+	4	D4
42m	42	2*2	D2d	DD8	[2+,4]	8	D4
mmm	22	*222	D2h	±D4	[2,2]	8	Z2×D4

Intl	Geo	Orbifold	Schönflies	Conway	Coxeter		Order	Abstract	Fund. domain
32 422 52 622	3.2 4.2 5.2 6.2 n.2	223 224 225 226 22n	D3 D4 D5 D6 Dn	D6 D8 D10 D12 D2n	[2,3]+ [2,4]+ [2,5]+ [2,6]+ [2,n]+		6 8 10 12 2n	D6 D8 D10 D12 D2n
3m 82m 5m 12.2m	62 82 10.2 12.2 n2	2*3 2*4 2*5 2*6 2*n	D3d D4d D5d D6d Dnd	±D6 DD16 ±D10 DD24 DD4n / ±D2n	[2+,6] [2+,8] [2+,10] [2+,12] [2+,2n]		12 16 20 24 4n	D12 D16 D20 D24 D4n
6m2 4/mmm 10m2 6/mmm	32 42 52 62 n2	*223 *224 *225 *226 *22n	D3h D4h D5h D6h Dnh	DD12 ±D8 DD20 ±D12 ±D2n / DD4n	[2,3] [2,4] [2,5] [2,6] [2,n]		12 16 20 24 4n	D12 Z2×D8 D20 Z2×D12 Z2×D2n ≅D4n (odd n)

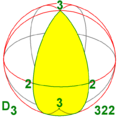
Polyhedral symmetry

Further information: Polyhedral groups

There are three types of polyhedral symmetry: tetrahedral symmetry, octahedral symmetry, and icosahedral symmetry, named after the triangle-faced regular polyhedra with these symmetries.

Tetrahedral symmetry

Intl	Geo	Orbifold	Schönflies	Conway	Coxeter	Order	Abstract	Fund. domain
23	3.3	332	T	T	[3,3]+	12	A4
m3	43	3*2	Th	±T	[4,3+]	24	2×A4
43m	33	*332	Td	TO	[3,3]	24	S4

Octahedral symmetry

Intl	Geo	Orbifold	Schönflies	Conway	Coxeter	Order	Abstract	Fund. domain
432	4.3	432	O	O	[4,3]+	24	S4
m3m	43	*432	Oh	±O	[4,3]	48	2×S4

Icosahedral symmetry

Intl	Geo	Orbifold	Schönflies	Conway	Coxeter	Order	Abstract	Fund. domain
532	5.3	532	I	I	[5,3]+	60	A5
532/m	53	*532	Ih	±I	[5,3]	120	2×A5

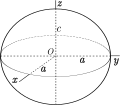
Continuous symmetries

All of the discrete point symmetries are subgroups of certain continuous symmetries. They can be classified as products of orthogonal groups O(n) or special orthogonal groups SO(n). O(1) is a single orthogonal reflection, dihedral symmetry order 2, Dih₁. SO(1) is just the identity. Half turns, C₂, are needed to complete.

Rank 3 groups	Other names	Example geometry		Example finite subgroups
O(3)		Full symmetry of the sphere		[3,3] = , [4,3] = , [5,3] = [4,3+] =
SO(3)	Sphere group	Rotational symmetry		[3,3]+ = , [4,3]+ = , [5,3]+ =
O(2)×O(1) O(2)⋊C2	Dih∞×Dih1 Dih∞⋊C2	Full symmetry of a spheroid, torus, cylinder, bicone or hyperboloid Full circular symmetry with half turn		[p,2] = [p]×[ ] = [2p,2+] = , [2p+,2+] =
SO(2)×O(1)	C∞×Dih1	Rotational symmetry with reflection		[p+,2] = [p]+×[ ] =
SO(2)⋊C2	C∞⋊C2	Rotational symmetry with half turn		[p,2]+ =
O(2)×SO(1)	Dih∞ Circular symmetry	Full symmetry of a hemisphere, cone, paraboloid or any surface of revolution		[p,1] = [p] =
SO(2)×SO(1)	C∞ Circle group	Rotational symmetry		[p,1]+ = [p]+ =

See also

• Crystallographic point group
• Triangle group
• List of planar symmetry groups
• Point groups in two dimensions

References

1. Johnson, 2015
2. Conway, John H. (2008). The symmetries of things. Wellesley, Mass: A.K. Peters. ISBN 978-1-56881-220-5. OCLC 181862605.
3. Conway, John; Smith, Derek A. (2003). On quaternions and octonions: their geometry, arithmetic, and symmetry. Natick, Mass: A.K. Peters. ISBN 978-1-56881-134-5. OCLC 560284450.
4. Sands, "Introduction to Crystallography", 1993

Further reading

• Peter R. Cromwell, Polyhedra (1997), Appendix I
• Sands, Donald E. (1993). "Crystal Systems and Geometry". Introduction to Crystallography. Mineola, New York: Dover Publications, Inc. p. 165. ISBN 0-486-67839-3.
• On Quaternions and Octonions, 2003, John Horton Conway and Derek A. Smith ISBN 978-1-56881-134-5
• The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ISBN 978-1-56881-220-5
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
  • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
  • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]
• N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite symmetry groups, Table 11.4 Finite Groups of Isometries in 3-space

External links

• Finite spherical symmetry groups
• Weisstein, Eric W. "Schoenflies symbol". MathWorld.
• Weisstein, Eric W. "Crystallographic point groups". MathWorld.
• Simplest Canonical Polyhedra of Each Symmetry Type, by David I. McCooey