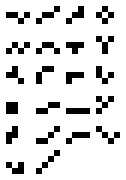Pseudo-polyomino

A pseudo-polyomino, also called a polyking, polyplet or hinged polyomino, is a plane geometric figure formed by joining one or more equal squares edge-to-edge or corner-to-corner at 90°. It is a polyform with square cells. The polyominoes are a subset of the polykings.

The 22 free tetrakings

The name "polyking" refers to the king in chess. The n-kings are the n-square shapes which could be occupied by a king on an infinite chessboard in the course of legal moves.

Golomb uses the term pseudo-polyomino referring to kingwise-connected sets of squares.^[1]

Enumeration of polykings

10 congruent mutilated chessboards 7x7 constructed with the 94 pseudo-pentominoes, or pentaplets

Free, one-sided, and fixed polykings

There are three common ways of distinguishing polyominoes and polykings for enumeration:^[1]

• free polykings are distinct when none is a rigid transformation (translation, rotation, reflection or glide reflection) of another (pieces that can be picked up and flipped over).
• one-sided polykings are distinct when none is a translation or rotation of another (pieces that cannot be flipped over).
• fixed polykings are distinct when none is a translation of another (pieces that can be neither flipped nor rotated).

The following table shows the numbers of polykings of various types with n cells.

n	free	one-sided	fixed
1	1	1	1
2	2	2	4
3	5	6	20
4	22	34	110
5	94	166	638
6	524	991	3832
7	3,031	5,931	23,592
8	18,770	37,196	147,941
9	118,133	235,456	940,982
10	758,381	1,514,618	6,053,180
11	4,915,652	9,826,177	39,299,408
12	32,149,296	64,284,947	257,105,146
OEIS	A030222	A030233	A006770

Free polykings

• 
  The 94 free pentakings.
• 
  The 524 free hexakings.
• 
  The 3,031 free heptakings.