Proof without words

In mathematics, a proof without words (or visual proof) is an illustration of an identity or mathematical statement which can be demonstrated as self-evident by a diagram without any accompanying explanatory text. Such proofs can be considered more elegant than formal or mathematically rigorous proofs due to their self-evident nature.^[1] When the diagram demonstrates a particular case of a general statement, to be a proof, it must be generalisable.^[2]

Proof without words of the Nicomachus theorem (Gulley (2010)) that the sum of the first n cubes is the square of the nth triangular number

A proof without words is not the same as a mathematical proof, because it omits the details of the logical argument it illustrates. However, it can provide valuable intuitions to the viewer that can help them formulate or better understand a true proof.

Examples

Sum of odd numbers

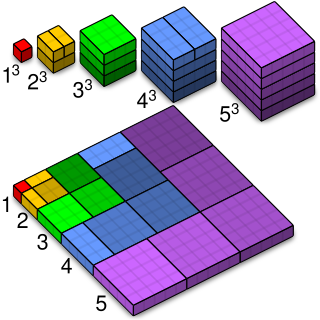
A proof without words for the sum of odd numbers theorem

The statement that the sum of all positive odd numbers up to 2n − 1 is a perfect square—more specifically, the perfect square n²—can be demonstrated by a proof without words.^[3]

In one corner of a grid, a single block represents 1, the first square. That can be wrapped on two sides by a strip of three blocks (the next odd number) to make a 2 × 2 block: 4, the second square. Adding a further five blocks makes a 3 × 3 block: 9, the third square. This process can be continued indefinitely.

Pythagorean theorem

Main article: Pythagorean theorem § Rearrangement proofs

Rearrangement proof of the Pythagorean theorem. The uncovered area of gray space remains constant before and after the rearrangement of the triangles: on the left it is shown to equal c², and on the right a²+b².

The Pythagorean theorem that ${\displaystyle a^{2}+b^{2}=c^{2}}$ can be proven without words.^[4]

One method of doing so is to visualise a larger square of sides ${\displaystyle a+b}$, with four right-angled triangles of sides ${\displaystyle a}$, ${\displaystyle b}$ and ${\displaystyle c}$ in its corners, such that the space in the middle is a diagonal square with an area of ${\displaystyle c^{2}}$. The four triangles can be rearranged within the larger square to split its unused space into two squares of ${\displaystyle a^{2}}$ and ${\displaystyle b^{2}}$.^[5]

Jensen's inequality

A graphical proof of Jensen's inequality

Jensen's inequality can also be proven graphically. A dashed curve along the X axis is the hypothetical distribution of X, while a dashed curve along the Y axis is the corresponding distribution of Y values. The convex mapping Y(X) increasingly "stretches" the distribution for increasing values of X.^[6]

Usage

Mathematics Magazine and The College Mathematics Journal run a regular feature titled "Proof without words" containing, as the title suggests, proofs without words.^[3] The Art of Problem Solving and USAMTS websites run Java applets illustrating proofs without words.^[7][8]

Compared to formal proofs

For a proof to be accepted by the mathematical community, it must logically show how the statement it aims to prove follows totally and inevitably from a set of assumptions.^[9] A proof without words might imply such an argument, but it does not make one directly, so it cannot take the place of a formal proof where one is required.^[10][11] Rather, mathematicians use proofs without words as illustrations and teaching aids for ideas that have already been proven formally.^[12][13]

See also

• Pizza theorem – Equality of areas of a sliced disk
• Philosophy of mathematics
• Proof theory – Branch of mathematical logic
• Visual calculus – Visual mathematical proofs