Umdeutung paper

In the history of physics, "On the quantum-theoretical reinterpretation of kinematical and mechanical relationships" (German: Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen), also known as the Umdeutung (reinterpretation) paper,^[1][2] was a breakthrough article in quantum mechanics written by Werner Heisenberg, which was published in Zeitschrift für Physik in July 1925.^[3]

Heisenberg 1926

In his article, Heisenberg described a new framework for quantum theory that was based on observable parameters such as transition probabilities or frequencies associated with quantum jumps rather than the unobservable parameters of electron orbits like position or velocity. Thus, Heisenberg used two indices for his re-interpretation of position, corresponding to initial and final states of quantum jumps. Heisenberg used his framework to successfully explain the energy levels of a one-dimensional anharmonic oscillator.^[4]: 153

Mathematically, Heisenberg used non-commutative operators in his new multiplication rule. This insight would later become the basis for Heisenberg's uncertainty principle.^{[citation needed]}

This article was followed by the paper by Max Born and Pascual Jordan of the same year, building on the conceptual ideas of the Umdeutung paper,^[5] and by the 'three-man paper' (German: Dreimännerarbeit) by Born, Heisenberg and Jordan in 1926.^[6][1][7] These following articles along with the Umdeutung paper laid the groundwork for matrix mechanics that would come to substitute old quantum theory, becoming the first mature mathematical formulation of quantum mechanics.^[8] Heisenberg received the Nobel Prize in Physics in 1932 for his work on developing quantum mechanics.^[9]

Historical context

Main article: History of quantum mechanics

The general narrative surrounding the Umdeutung paper states that Heisenberg, then 23 years old, worked on the article whilst recovering from hay fever on the largely vegetation-free island of Heligoland for about 10 days after arriving on June 6 1925, where he had a 'eureka moment' discovery that lead to mature quantum mechanics.^[10][11] However, this narrative has been criticised for stemming from Heisenberg's account in his 1969 to 1971 memoirs, where Heisenberg stated his book was written in broad historical terms without precise detail.^[12] It has been argued that Heisenberg's account is hard to reconcile with contemporary evidence and that the majority of the paper was likely written after Heisenberg's stay on Heligoland in the first weeks of July.^[1]

It has also been argued that the idea of a 'eureka' discovery conflicts with Heisenberg's frequent correspondence with Wolfgang Pauli on his paper that expressed uncertainty.^[12]. When asked for his opinion of the manuscript, Pauli responded favorably, but Heisenberg said that he was still "very uncertain about it". In July 1925, he sent the manuscript to Max Born to review and decide whether to submit it for publication.^[13] The idealisation of Heisenberg's work as a 'eureka' breakthrough has also been seen as disproportional when compared to the work other physicists made at the same time.^[14]

In classical physics, the intensity of each frequency of light produced in a radiating system is equal to the square of the amplitude of the radiation at that frequency, so attention next fell on amplitudes. The classical equations that Heisenberg hoped to use to form quantum theoretical equations would first yield the amplitudes, and in classical physics one could compute the intensities simply by squaring the amplitudes. But Heisenberg saw that "the simplest and most natural assumption would be"^[15]: 275f to follow the lead provided by recent work in computing light dispersion done by Hans Kramers.^[16] The work he had done assisting Kramers in the previous year^{[15]: paper 3} now gave him an important clue about how to model what happened to excited hydrogen gas when it radiated light and what happened when incoming radiation of one frequency excited atoms in a dispersive medium and then the energy delivered by the incoming light was re-radiated – sometimes at the original frequency but often at two lower frequencies the sum of which equalled the original frequency. According to their model, an electron that had been driven to a higher energy state by accepting the energy of an incoming photon might return in one step to its equilibrium position, re-radiating a photon of the same frequency, or it might return in more than one step, radiating one photon for each step in its return to its equilibrium state. Because of the way factors cancel out in deriving the new equation based on these considerations, the result turns out to be relatively simple.

Heisenberg was not the only physicist close to making a breakthrough on developing quantum mechanics in 1925; Van Vleck, in his two-part paper of 1924, used the correspondence principle as well as similar methods to Kramers and Heisenberg's dispersion paper, which however has been rarely commented on in secondary literature.^[14]

Description

Heisenberg's re-interpretation of quantum theory

One of the key aspects of Heisenberg's paper in forming a new quantum theory was its deliberate choice to not utilise unobserved quantities such as the electron's position and period but only to utilise observable parameters like transition probabilities or spectral frequencies.^[15][17] Whilst some have seen this as one of the succeeding innovations of Heisenberg's paper, others have viewed the correspondence principle as the primary driver of Heisenberg's argument.^[18][19] His letter to Kronig one month before the publishing of the Umdeutung paper closely follows the same structure as the paper but emphasises the correspondence of the Fourier coefficients rather than the philosophical focus on observable quantities.^[20]

An electron falling from energy state 3 to energy state 2 (left) emits a photon. The wavelength is given by the Rydberg formula (middle). Calculating the wavelength for hydrogen energy levels, it correspond to a red photon (right). The important question was what will be the intensity of radiation in the spectrum at that wavelength?

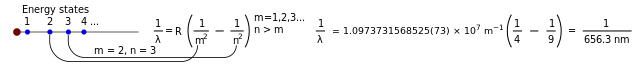
Fourier re-interpretation

Classically, a periodic orbit for an electron in stationary state ${\displaystyle n}$ may be described as$${\displaystyle x=\sum _{\alpha =-\infty }^{\infty }{\vec {X}}_{\alpha }(n)e^{i\alpha \omega (n)t}}$$ using a Fourier series, where ${\vec {X}}_{-\alpha }(n)={\vec {X}}_{\alpha }^{*}(n)$ (${\vec {X}}^{*}$ is the complex conjugate) for $x_{\alpha }$ to be real-valued.^[21]

Heisenberg decides to re-interpret this for his quantum theory to be^[22]

Heisenberg's equation for position

${\displaystyle x=\sum _{\alpha =-\infty }^{\infty }{\vec {X}}(n,n-\alpha )e^{i\omega (n,n-\alpha )t}}$

where ${\displaystyle \omega (n,n-\alpha )}$ represents the frequency of light emitted/absorbed and ${\displaystyle {\vec {X}}(n,n-\alpha )}$ represents an intensity relating to transition probabilities when there is a transition from stationary state ${\displaystyle n}$ to ${\displaystyle n-\alpha }$. Heisenberg mentions that ${\displaystyle \omega (n,n-\alpha )}$ may be found using the Bohr model calculation of $${\displaystyle \omega (n,n-\alpha )={\frac {1}{\hbar }}[W(n)-W(n-\alpha )]}$$ where ${\displaystyle W(n)}$ is the energy of a given stationary state ${\displaystyle n}$.^[23]

A justification for Heisenberg's Fourier re-interpretation can be seen when comparing classical and quantum expressions for the orbital frequencies. Classically, using action-angle variables, it can be found that $${\displaystyle \alpha \omega =\lim _{\epsilon \to 0}{\frac {E(J+\alpha \epsilon )-E(J)}{\epsilon }},\quad \alpha \in \mathbb {Z} }$$ as ${\displaystyle dE/dJ=\omega }$; in the Bohr model, by contrast, it is found that $${\displaystyle \omega (n,n-\alpha )={\frac {E(n\hbar )-E((n-\alpha )\hbar )}{\hbar }},\quad (E(J)=E(n\hbar )).}$$ Using the correspondence principle $${\displaystyle \omega ={\frac {dE}{dJ}}\to {\frac {\Delta E}{\Delta J}}}$$ it can be found $${\displaystyle (n-(n-\alpha ))\omega =\alpha \omega (n)\approx {\frac {E(n\hbar )-E((n-\alpha )\hbar )}{\hbar }},\quad |\alpha -n|\ll \alpha .}$$ using ${\displaystyle J=n\hbar }$ from the old quantum theory.^[24] This correspondence between ${\displaystyle \omega (n,n-\alpha )}$ and ${\displaystyle \alpha \omega (n)}$ also suggests a correspondence between the intensities ${\displaystyle {\vec {X}}(n,n-\alpha )}$ and ${\displaystyle {\vec {X}}_{\alpha }(n)}$ in the connection $${\displaystyle x=\sum _{\alpha =-\infty }^{\infty }{\vec {X}}_{\alpha }(n)e^{i\alpha \omega (n)t}\longleftrightarrow x=\sum _{\alpha =-\infty }^{\infty }{\vec {X}}(n,n-\alpha )e^{i\omega (n,n-\alpha )t}.}$$

This Fourier re-interpretation was also justified in Heisenberg's view so that the electron in its periodic motion, which the Bohr model predicted, would not have a single characteristic radiation frequency ${\displaystyle \omega (n)}$ in stationary state ${\displaystyle n}$ that had never been experimentally measured. Under Heisenberg's re-interpretation, the motion of the electron would only have the experimentally observed spectral frequencies ${\displaystyle \omega (n,n-\alpha )}$ as components of its periodic motion. Heisenberg notes, however, that by the publishing of the paper that the electronic orbit was abandoned as physically meaningful.^[25]

Non-commutative multiplication rule

Heisenberg uses the Rydberg–Ritz combination principle as a fundamental part of how frequencies should behave in his quantum theory. Rather than the classical rule $${\displaystyle \omega (n,\alpha )+\omega (n,\beta )=\omega (n,\alpha +\beta ),}$$ Heisenberg writes out the Ritz combination principle $${\displaystyle \omega (n,n-\alpha )+\omega (n-\alpha ,n-\beta )=\omega (n,n-\beta ).}$$ ^[26].

Classically, multiplying two position Fourier series together forms a new Fourier series: $${\displaystyle \sum _{\tau }a_{\tau }e^{i\omega \tau t}\times \sum _{\tau }b_{\tau }e^{i\omega \tau t}=\sum _{\tau }c_{\tau }e^{i\omega \tau t}}$$ where $${\displaystyle c_{\tau }=\sum _{\tau '+\tau ''=\tau }a_{\tau '}b_{\tau ''}.}$$^[27]

Heisenberg analogised from this classical case that multiplying two quantum series should give another quantum series of the same form. In other words, Heisenberg finds that if a quantum series may be written $${\displaystyle x=\sum _{\alpha =-\infty }^{\infty }{\vec {X}}(n,n-\alpha )e^{i\omega (n,n-\alpha )t},}$$then $${\displaystyle x^{2}=\sum _{\beta =-\infty }^{\infty }{\vec {B}}(n,n-\beta )e^{i\omega (n,n-\beta )t}.}$$

Whilst a normal multiplication would not work to form a new quantum series, Heisenberg deliberately re-interprets multiplication to be now following the new quantum multiplication rule $${\displaystyle {\vec {B}}(n,n-\beta )=\sum _{\alpha }{\vec {X}}(n,n-\alpha )\times {\vec {X}}(n-\alpha ,n-\beta ).}$$ ^{[1]: 223–224  [20]}

This is so that $${\displaystyle e^{i\omega (n,n-\alpha )t}\times e^{i\omega (n-\alpha ,n-\beta )}=e^{it(\omega (n,n-\alpha )+\omega (n-\alpha ,n-\beta ))}=e^{it\omega (n,n-\beta )}}$$ using the earlier Rydberg-Ritz Combination Rule ${\displaystyle \omega (n,n-\alpha )+\omega (n-\alpha ,n-\beta )=\omega (n,n-\beta )}$ so that all the frequencies ${\displaystyle \omega (n,n-\beta )}$ are correct for the new series.^[19]

Intensities of the visible spectrum of a hydrogen plasma obtained with Ocean Optics USB2000 low resolution spectrometer. Alpha, Beta, Gamma Balmer lines are visible, other lines are indistinguishable from the noise.

Generalizing from the earlier multiplication case of ${\displaystyle x^{2}}$, Heisenberg wrote out his new, non-commutative multiplication rule that is the quantum mechanical analog for the classical computation of intensities:^{[15]: 266 [28]: 5 [22]}

Heisenberg's non-commutative multiplication rule

${\displaystyle {\vec {C}}(n,n-\beta )=\sum _{\alpha }{\vec {A}}(n,n-\alpha )\times {\vec {B}}(n-\alpha ,n-\beta ).}$

There will potentially be an infinite series of ${\displaystyle {\vec {A}}}$ terms and their matching ${\displaystyle {\vec {B}}}$ terms. Each of these multiplications has as its factors two measurements that pertain to sequential downward transitions between energy states of an electron. This type of rule differentiates matrix mechanics from the kind of physics familiar in everyday life because the important values are where (in what energy state or "orbital") the electron begins and in what energy state it ends, not what the electron is doing while in one or another state.

If ${\displaystyle {\vec {A}}}$and ${\displaystyle {\vec {B}}}$ both refer to lists of frequencies, for instance, the calculation proceeds as follows:

Multiply the frequency for a change of energy from state n to state n − a by the frequency for a change of energy from state n − a to state n − b, and to that add the product found by multiplying the frequency for a change of energy from state n − a to state n − b by the frequency for a change of energy from state n − b to state n − c, and so forth. Symbolically, that is:

${\displaystyle f(n,n-a)f(n-a,n-b)+f(n-a,n-b)f(n-b,n-c)+\cdots }$

(According to the convention used, n − a represents a higher energy state than n, so a transition from n to n − a would indicate that an electron has accepted energy from an incoming photon and has risen to a higher orbital, while a transition from n − a to n would represent an electron falling to a lower orbital and emitting a photon.)

It would be easy to perform each individual step of this process for some measured quantity. For instance, the boxed formula at the head of this article gives each needed wavelength in sequence. The values calculated could very easily be filled into a grid as described below. However, since the series is infinite, nobody could do the entire set of calculations.

Heisenberg originally devised this equation to enable himself to multiply two measurements of the same kind (amplitudes), so it happened not to matter in which order they were multiplied. Heisenberg noticed, however that if he tried to use the same schema to multiply two variables, such as momentum, p, and displacement, q, then "a significant difficulty arises".^[15]: 266 It turns out that multiplying a matrix of p by a matrix of q gives a different result from multiplying a matrix of q by a matrix of p. It only made a tiny bit of difference, but that difference could never be reduced below a certain limit, and that limit involved the Planck constant, h.

Motion

Heisenberg also notes that, in the old quantum theory, the observable quantities are solved from Newton's Second Law $${\displaystyle {\ddot {x}}+f(x)=0}$$ and the Wilson–Sommerfeld quantisation rule $${\displaystyle \oint pdq=\oint m{\dot {x}}dx=\oint m{\dot {x}}^{2}dt=J=(nh).}$$ where ${\displaystyle f(x)}$ is the force per unit mass function, where Heisenberg then makes the assumption that using his new Fourier re-interpretation of ${\displaystyle x}$ that the same Newtonian equations may be used to solve for observable quantities.^[19]

Quantisation

As a part of Heisenberg's justification for a theory of mechanics that is only reliant on the intensities and frequencies that are measurable, Heisenberg derives the Thomas-Reiche-Kuhn sum rule found from studying dispersion^[23]

Heisenberg's quantisation rule

${\displaystyle 4\pi hm=\sum _{\alpha =0}^{\infty }\{|a(n,n+\alpha )|^{2}\omega (n,n+\alpha )-|a(n,n-\alpha )|^{2}\omega (n,n-\alpha )\}}$

for ${\displaystyle x=\sum _{\alpha =-\infty }^{\infty }a(n,n-\alpha )e^{i\omega (n,n-\alpha )t}}$. ^[19]

Quantum anharmonic oscillator

Heisenberg additionally studies the energy levels of the anharmonic oscillator described by ${\displaystyle {\ddot {x}}+\omega _{0}^{2}x+\lambda x^{2}=0}$, as the conceptually more simple harmonic oscillator would not have required his new multiplication rule.^[29] Whereas under a classical consideration he finds that ${\displaystyle E_{n}=n\hbar \omega _{0}}$, but under a quantum consideration using the theory developed in his paper, up to order ${\displaystyle \lambda ^{2}}$, he finds that $${\displaystyle E_{n}=n\hbar \left(\omega _{0}+{\frac {1}{2}}\right),}$$ explaining the existence of zero-point energy that had already been inferred from experiment.^[30] The lack of dependence on ${\displaystyle \lambda }$ made the equation written allowed to be used for the energy levels of the harmonic oscillator (${\displaystyle \lambda =0}$) as well. Heisenberg would also extend this equation to the electron rotating at angular frequency ${\displaystyle \omega }$ around the nucleus to find^[29] $${\displaystyle \omega _{n,n-1}={\frac {h}{2\pi ma^{2}}}n}$$ and for the energy ${\displaystyle W}$ $${\displaystyle W={\frac {h^{2}}{8\pi ^{2}ma^{2}}}(n^{2}+n+{\frac {1}{2}})}$$ in agreement with experimental observations by Adolf Kratzer.

Legacy

Development of matrix mechanics

Visible spectrum of hydrogen.

The one thing that people at that time most wanted to understand about hydrogen radiation was how to predict or account for the intensities of the lines in its spectrum. Although Heisenberg did not know it at the time, the general format he worked out to express his new way of working with quantum theoretical calculations can serve as a recipe for two matrices and how to multiply them.^{[15]: Ch 12}

The Umdeutung paper does not mention matrices. Heisenberg's great advance was the "scheme which was capable in principle of determining uniquely the relevant physical qualities (transition frequencies and amplitudes)"^[28]: 2 of hydrogen radiation.

After Heisenberg wrote the Umdeutung paper, he turned it over to one of his senior colleagues for any needed corrections and went on vacation. Max Born puzzled over the equations and the non-commuting equations that Heisenberg had found troublesome and disturbing. After several days he realized that these equations amounted to directions for writing out matrices.^[31]

By consideration of ... examples. .. [Heisenberg] found this rule ... This was in the summer of 1925. Heisenberg ... took leave of absence ... and handed over his paper to me for publication ... Heisenberg's rule of multiplication left me no peace, and after a week of intensive thought and trial, I suddenly remembered an algebraic theory....Such quadratic arrays are quite familiar to mathematicians and are called matrices, in association with a definite rule of multiplication. I applied this rule to Heisenberg's quantum condition and found that it agreed for the diagonal elements. It was easy to guess what the remaining elements must be, namely, null; and immediately there stood before me the strange formula $${\displaystyle {QP-PQ={\frac {ih}{2\pi }}}}$$

The symbol Q is the matrix for displacement, P is the matrix for momentum, i stands for the square root of negative one, and h is the Planck constant.^{[32][28]: A} Born and a few colleagues took up the task of working everything out in matrix form before Heisenberg returned from his time off, and within a few months the new quantum mechanics in matrix form formed the basis for another paper.

When Born read the article, he recognized the formulation as one which could be transcribed and extended to the systematic language of matrices. Born, with the help of his assistant and former student Pascual Jordan, began immediately to make the transcription and extension, and they submitted their results for publication; their manuscript was received for publication just 60 days after Heisenberg’s article.^[5] A follow-on article by all three authors extending the theory to multiple dimensions was submitted for publication before the end of the year.^[6]

Paul Dirac, who had received a proof copy in August 1925, realized that the non-commutative law had not been fully developed, and he produced an algebraic formulation to express the same results in more logical form.^[33] His insight led to new and productive directions in developing quantum mechanics.^[34]

"Magical paper"

Steven Weinberg would later name Heisenberg's paper as "pure magic" due to Heisenberg's lack of written motivation that he takes in justifying each mathematical step, leaving the reader "mystified" despite the successful predictions of Heisenberg's framework.^[35] A number of attempts have been made to explain his paper more accessibly.^[3]

See also

• History of quantum mechanics
• Mathematical formulation of quantum mechanics