Scorer's function

In mathematics, the Scorer's functions are special functions studied by Scorer (1950) and denoted Gi(x) and Hi(x).

Graph of ${\displaystyle \mathrm {Gi} (x)}$ and ${\displaystyle \mathrm {Hi} (x)}$

Hi(x) and -Gi(x) solve the equation

${\displaystyle y''(x)-x\ y(x)={\frac {1}{\pi }}}$

and are given by

${\displaystyle \mathrm {Gi} (x)={\frac {1}{\pi }}\int _{0}^{\infty }\sin \left({\frac {t^{3}}{3}}+xt\right)\,dt,}$

${\displaystyle \mathrm {Hi} (x)={\frac {1}{\pi }}\int _{0}^{\infty }\exp \left(-{\frac {t^{3}}{3}}+xt\right)\,dt.}$

The Scorer's functions can also be defined in terms of Airy functions:

${\displaystyle {\begin{aligned}\mathrm {Gi} (x)&{}=\mathrm {Bi} (x)\int _{x}^{\infty }\mathrm {Ai} (t)\,dt+\mathrm {Ai} (x)\int _{0}^{x}\mathrm {Bi} (t)\,dt,\\\mathrm {Hi} (x)&{}=\mathrm {Bi} (x)\int _{-\infty }^{x}\mathrm {Ai} (t)\,dt-\mathrm {Ai} (x)\int _{-\infty }^{x}\mathrm {Bi} (t)\,dt.\end{aligned}}}$

It can also be seen, just from the integral forms, that the following relationship holds:

${\displaystyle \mathrm {Gi} (x)+\mathrm {Hi} (x)\equiv \mathrm {Bi} (x)}$

• 
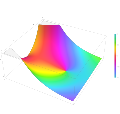
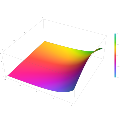
  Plot of the Scorer function Gi(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
• 
  Plot of the derivative of the Scorer function Hi'(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
• 
  Plot of the derivative of the Scorer function Gi'(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
• 
  Plot of the Scorer function Hi(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D

References

• Olver, F. W. J. (2010), "Scorer functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
• Scorer, R. S. (1950), "Numerical evaluation of integrals of the form ${\displaystyle I=\int _{x_{1}}^{x_{2}}f(x)e^{i\phi (x)}dx}$ and the tabulation of the function ${\displaystyle {\rm {Gi}}(z)={\frac {1}{\pi }}\int _{0}^{\infty }{\rm {sin}}\left(uz+{\frac {1}{3}}u^{3}\right)du}$", The Quarterly Journal of Mechanics and Applied Mathematics, 3: 107–112, doi:10.1093/qjmam/3.1.107, ISSN 0033-5614, MR 0037604