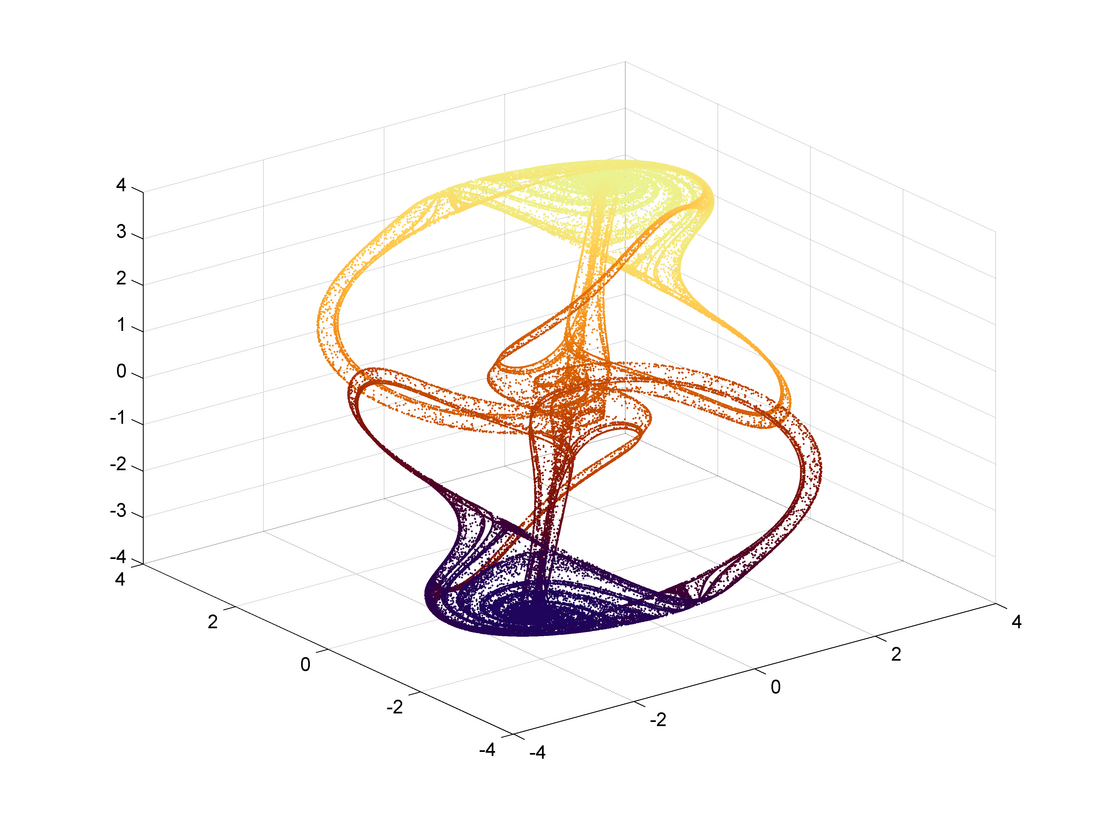
Thomas' cyclically symmetric attractor

In the dynamical systems theory, Thomas' cyclically symmetric attractor is a 3D strange attractor originally proposed by René Thomas.^[1] It has a simple form which is cyclically symmetric in the x, y, and z variables and can be viewed as the trajectory of a frictionally dampened particle moving in a 3D lattice of forces.^[2] The simple form has made it a popular example.

Thomas' cyclically symmetric attractor.

It is described by the differential equations

${\displaystyle {\frac {dx}{dt}}=\sin(y)-bx}$

${\displaystyle {\frac {dy}{dt}}=\sin(z)-by}$

${\displaystyle {\frac {dz}{dt}}=\sin(x)-bz}$

where ${\displaystyle b}$ is a constant.

${\displaystyle b}$ corresponds to how dissipative the system is, and acts as a bifurcation parameter. For ${\displaystyle b>1}$ the origin is the single stable equilibrium. At ${\displaystyle b=1}$ it undergoes a pitchfork bifurcation, splitting into two attractive fixed points. As the parameter is decreased further they undergo a Hopf bifurcation at ${\displaystyle b\approx 0.32899}$, creating a stable limit cycle. The limit cycle then undergoes a period doubling cascade and becomes chaotic at ${\displaystyle b\approx 0.208186}$. Beyond this the attractor expands, undergoing a series of crises (up to six separate attractors can coexist for certain values). The fractal dimension of the attractor increases towards 3.^[2]

In the limit ${\displaystyle b=0}$ the system lacks dissipation and the trajectory ergodically wanders the entire space (with an exception for 1.67%, where it drifts parallel to one of the coordinate axes: this corresponds to quasiperiodic torii). The dynamics has been described as deterministic fractional Brownian motion, and exhibits anomalous diffusion.^[2][3]