In category theory, a traced monoidal category is a category with some extra structure which gives a reasonable notion of feedback.
A traced symmetric monoidal category is a symmetric monoidal category C together with a family of functions

called a trace, satisfying the following conditions:
- naturality in
 : for every
: for every  and
and  ,
,

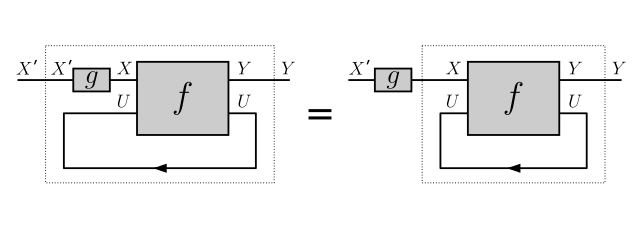 Naturality in X
Naturality in X
- naturality in
 : for every
: for every  and
and  ,
,

 Naturality in Y
Naturality in Y
- dinaturality in
 : for every
: for every  and
and 

 Dinaturality in U
Dinaturality in U
- vanishing I: for every
 , (with
, (with  being the right unitor),
being the right unitor),

 Vanishing I
Vanishing I
- vanishing II: for every


 Vanishing II
Vanishing II
- superposing: for every
 and
and  ,
,

 Superposing
Superposing

(where  is the symmetry of the monoidal category).
is the symmetry of the monoidal category).
 Yanking
Yanking




























