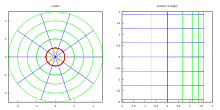
In mathematics, a complex logarithm is a generalization of the natural logarithm to nonzero complex numbers. The term refers to one of the following, which are strongly related:A complex logarithm of a nonzero complex number , defined to be any complex number for which . Such a number is denoted by . If is given in polar form as , where and are real numbers with , then is one logarithm of , and all the complex logarithms of are exactly the numbers of the form for integers . These logarithms are equally spaced along a vertical line in the complex plane. A complex-valued function , defined on some subset of the set of nonzero complex numbers, satisfying for all in . Such complex logarithm functions are analogous to the real logarithm function , which is the inverse of the real exponential function and hence satisfies eln x = x for all positive real numbers x. Complex logarithm functions can be constructed by explicit formulas involving real-valued functions, by integration of , or by the process of analytic continuation.