Senfinecona kalkulo

Infinitezima kalkulo aŭ senfinecona kalkulo estas branĉo de matematiko, kiu entenas la diferencialan kalkulon, kiu interalie temas pri la determinado de tangentoj de kurbo, kaj la integralan kalkulon, kiu interalie temas pri kalkulado de areoj kaj kurblongoj. Ili estas kunigitaj per la fundamenta teoremo de senfinecona kalkulo, kiu diras ke la la nedifinita integralo de funkcio ĉiam estas malderivaĵo de tiu funkcio, do ke funkcio f estas la derivaĵo de la nedifinita integralo de f. La matematike rigoran formon de senfinecona kalkulo oni kutime nomas analitiko.

La senfineconan kalkulon malkovris en la 17-a jarcento Newton kaj Leibniz. Newton estis la unua homo kiu uzis ĝin por analizi problemojn de fiziko, kaj Leibniz kreis la simbolon por integraloj kiu ankoraŭ estas uzata hodiaŭ. Ambaŭ viroj malkovris ĝin sendepende, sed Leibniz publikigis ĝin unue, estigante grandan malkonsenton pri kiu vere malkovris ĝin, kaj pri la demando ĉu Leibniz ŝtelis la malkovron de Newton.

Diferenciala kalkulo

Ĉefa artikolo: Diferenciala kalkulo

La ĉefa objekto kiun oni studas en diferenciala kalkulo estas la derivaĵo. La derivaĵo ${\displaystyle f'(x_{0})}$ de la funkcio ${\displaystyle f:A\subseteq \mathbb {R} \rightarrow \mathbb {R} }$ ĉe la punkto ${\displaystyle x_{0}\in A}$ oni difinas kiel limvaloron de diferenca kvociento. Kiam tiu ĉi limvaloro ekzistas, oni diras ke la funkcio estas derivebla ĉe tiu punkto. Se la limvaloro ne ekzistas, la funkcio ne havas derivaĵo ĉe tiu punkto.

${\displaystyle f'(x_{0})={\frac {df}{dx}}|_{x=x_{0}}=\lim _{h\rightarrow 0}{\frac {f(x_{0}+h)-f(x_{0})}{h}}}$

La simbolon ${\displaystyle df/dx}$ kreis Leibniz por reprezenti derivaĵojn, ĉar laŭ li, derivaĵoj estis kvocientoj de du senfineconaj ŝanĝoj: la ŝanĝon ${\displaystyle df}$ kaŭzis la ŝanĝo ${\displaystyle dx}$. Hodiaŭ tiuj ĉi diferencialoj havas alian signifon.

Integrala kalkulo

Ĉefa artikolo: Integrala kalkulo

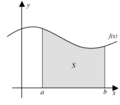
La ĉefa objekto kiun oni studas en integrala kalkulo estas la integralo. Se oni havas funkcio ${\displaystyle f:[a,b]\rightarrow \mathbb {R} }$ kiu estas kontinua sur ${\displaystyle [a,b]}$, oni povas difini la integralon rigore kiel la limvaloron de la tuta areo de rektanguloj sub la kurbo desegnita de la funkcio, kies bazoj fariĝas pli kaj pli etaj. Oni skribas tiun ĉi limvaloron per la jena simbolo:

${\displaystyle \int _{a}^{b}f(x)dx}$

Ankaŭ tiun ĉi reprezentiĝon kreis Leibniz, ĉar laŭ li, integraloj estis kunaĵo de multaj senfinecone maldikaj rektanguloj, kies bazo estis ${\displaystyle dx}$ kaj kies alteco estis ${\displaystyle f(x)}$.

Bildaro

• 
  Isaac Newton
• 
  Gottfried Wilhelm Leibniz
• 
  Isaac Newton
• 

Vidu ankaŭ

• Limeso
• Multvariebla kalkulo
• Derivaĵo
• Senfinecono
• Variada kalkulo
• Isaac Barrow

Eksteraj ligiloj

• Kategorio Senfinecona kalkulo en la Vikimedia Komunejo (Multrimedaj datumoj)
• Senfinecona kalkulo en la Vikicitaro (Kolekto de citaĵoj)

• http://www.ericdigests.org/pre-9217/calculus.htm Arkivigite je 2021-07-26 per la retarkivo Wayback Machine
• http://ory.ph.biu.ac.il/~havlin/math_book.php3 Arkivigite je 2006-06-24 per la retarkivo Wayback Machine
• http://math.eitan.ac.il/infi1
• http://bpec.our168.com/wjf/index.php Arkivigite je 2006-01-03 per la retarkivo Wayback Machine